涵盖了各种排序算法,包括选择排序、堆排序、合并排序、插入排序、shellsort、quicksort、分区、快速选择、稳定性、子数排序、计数排序、压缩等。文章还深入探讨了排序的定义和排序关系的属性,以及无前缀编码和哈夫曼编码。此外,它还包括压缩理论和软件工程方面的信息。
这个博客并不是我最初写这篇笔记地方,所以可能出现各种包括发布时间、文字、样式等错误
Week 12 & 13
排序的定义
对于key:a、b和c的排序关系“<”具有以下属性。
三分法:a < b, a = b, b < a中只有一个是真的。
跨度法则:如果a<b,并且b<c,那么a<c
上述属性的排序关系也被称为全序关系 (Total order)
另一个定义,inversion(倒转)的元素,排序就是将然倒转了的元素对不断减少最终变为0
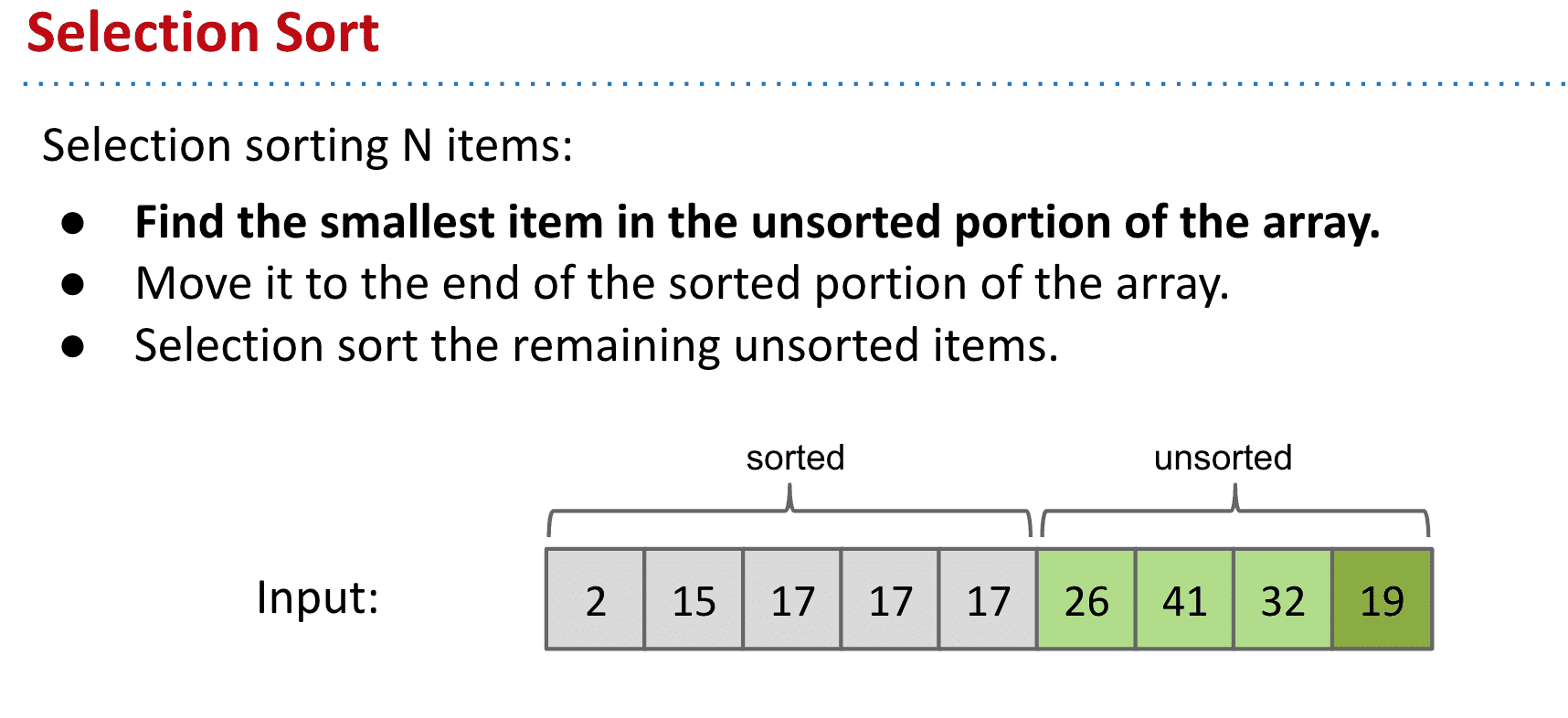
效率很低,如果使用数组来进行需要Θ(N^2)
选择排序可视化:
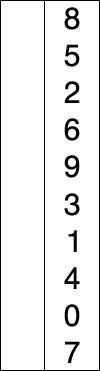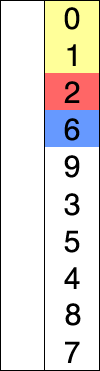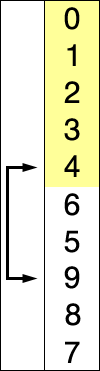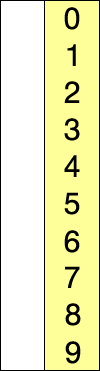

(所有排序可视化图片均来自wikipedia)
堆排序 Heapsort: 放入一个Max BST再取出
堆大概就是一个二叉树父节点总是大于/小于子节点
Max Heap 是一种特殊的堆数据结构,其中每个父节点的关键字都大于等于它的子节点。因此,堆顶元素始终是当前堆中最大的元素。
在最大堆中,父节点的关键字是大于等于它的左右子节点。换句话说,最大堆是一种完全二叉树,其中每个父节点的关键字都大于等于它的左右子节点。
简单的堆排序
使用max heap存储数据再放入新的list就得到了排序

这样就不会像选择排序那样每次看了大量内容却只使用最小的浪费时间
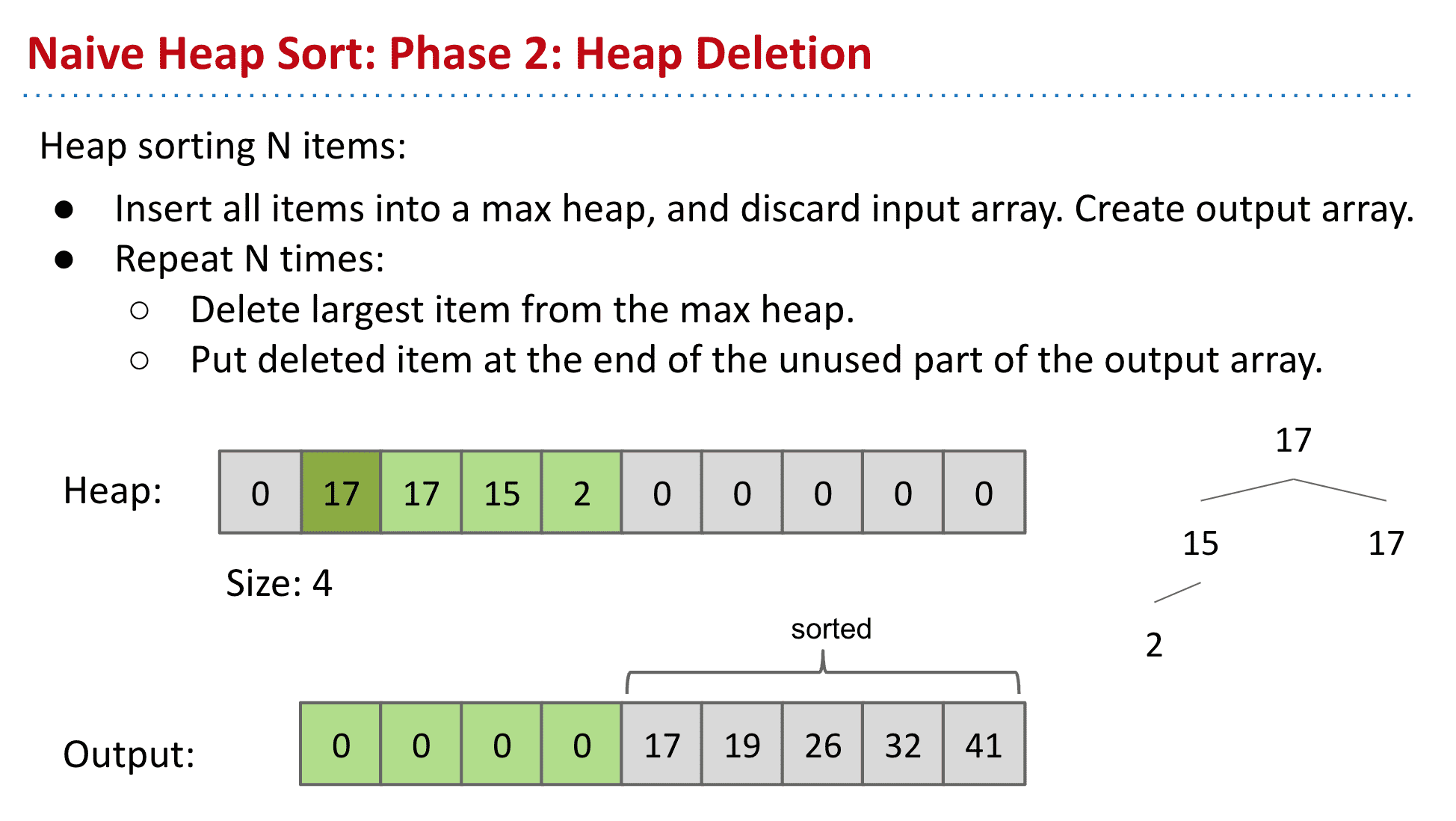
max heap的排序的大的在前小的在后,然后按顺序放入output末尾就完成了堆排序
运行时间比选择排序快!

不需要额外空间的堆排序(真正被使用的)
不使用额外的数组,而是在本身进行操作
分为两个步骤:
1.Bottom-up heapify input array.
2.重复多次:Delete largest item from the max heap, swapping root with last item in the heap.

首先使用一种叫Bottom-up heapify input array
从下而上变成一个个小的heap
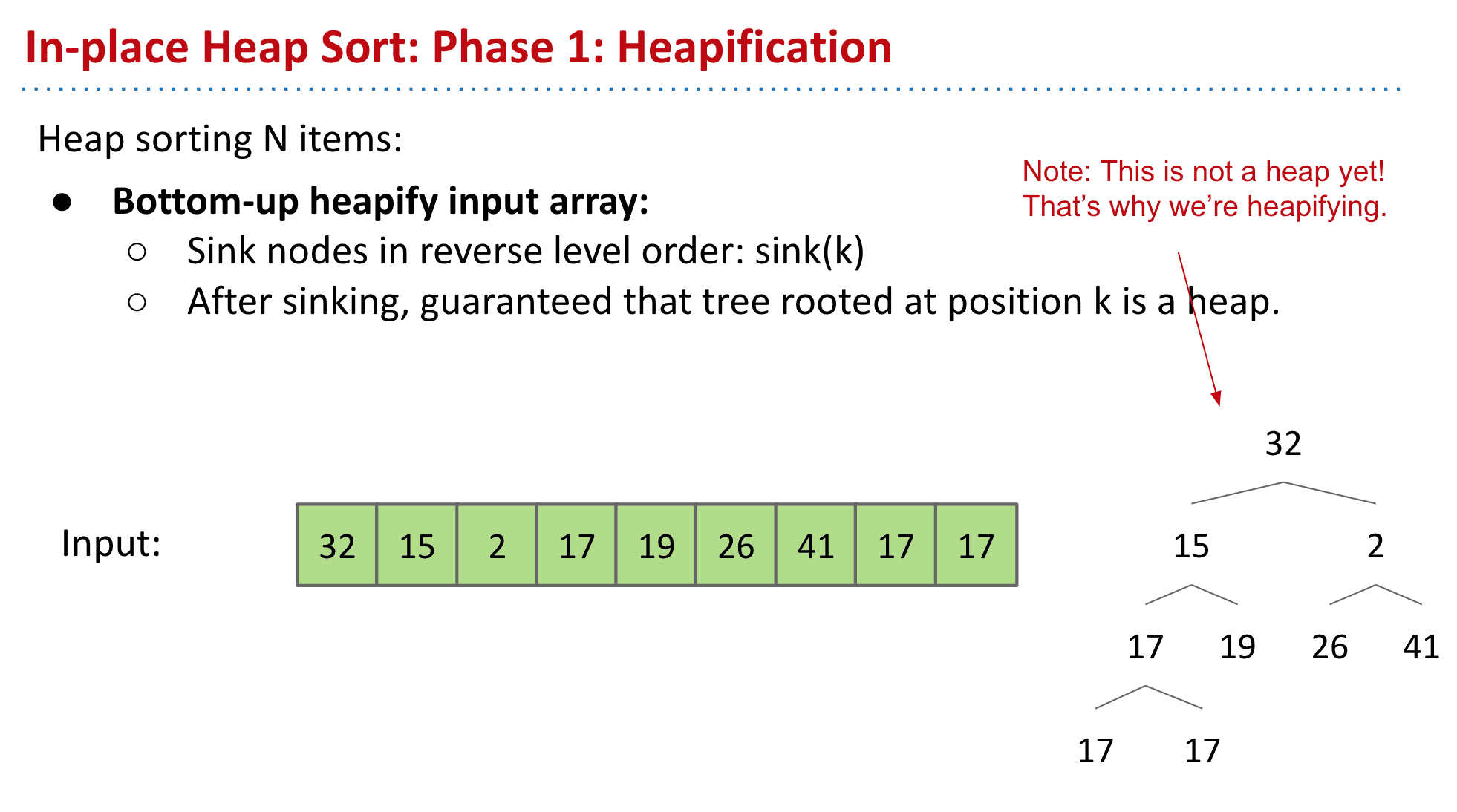
比如17、17、19、26、41都相当于一个子heap
于是再向上一层,又是一个17
就组成了一个新的子heap
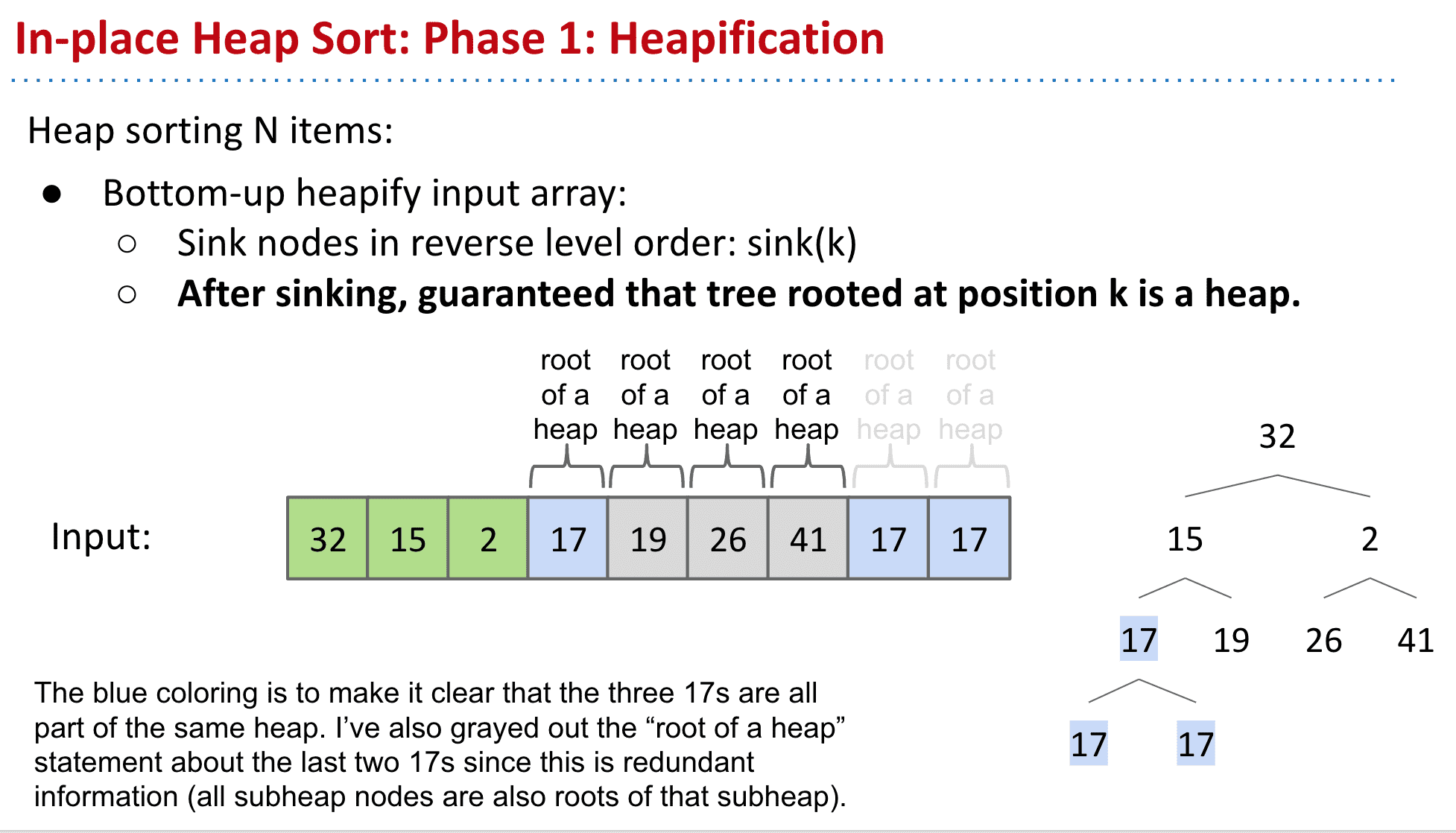
接下来到达2发现它不适合作为2→26、41的heap的root,所以和41调换
(这一步也可以叫做sinking,就是把每一个绿节点都和下面的比较看看能不能沉下去,能的话就调换)
形成了新的子heap 41→26、2
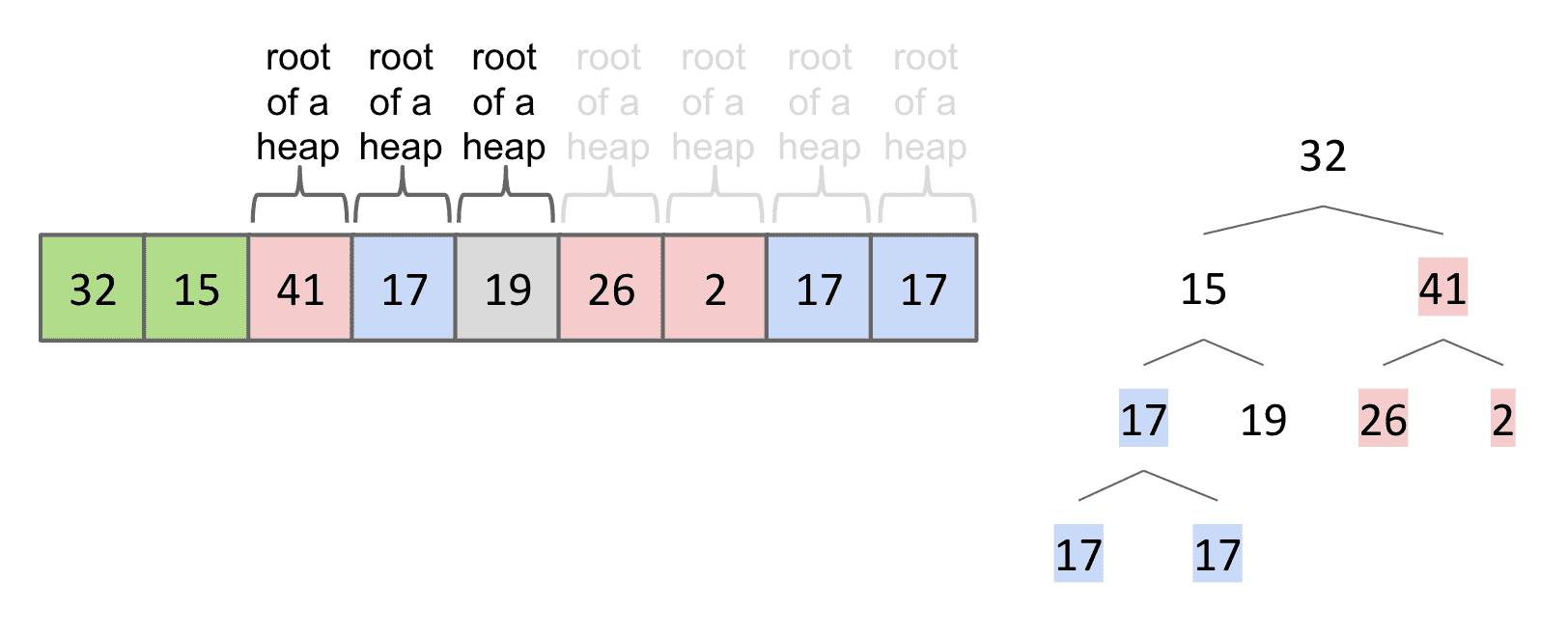
这样不断向上操作就得到了一个Max Heap(但是还有没排序)
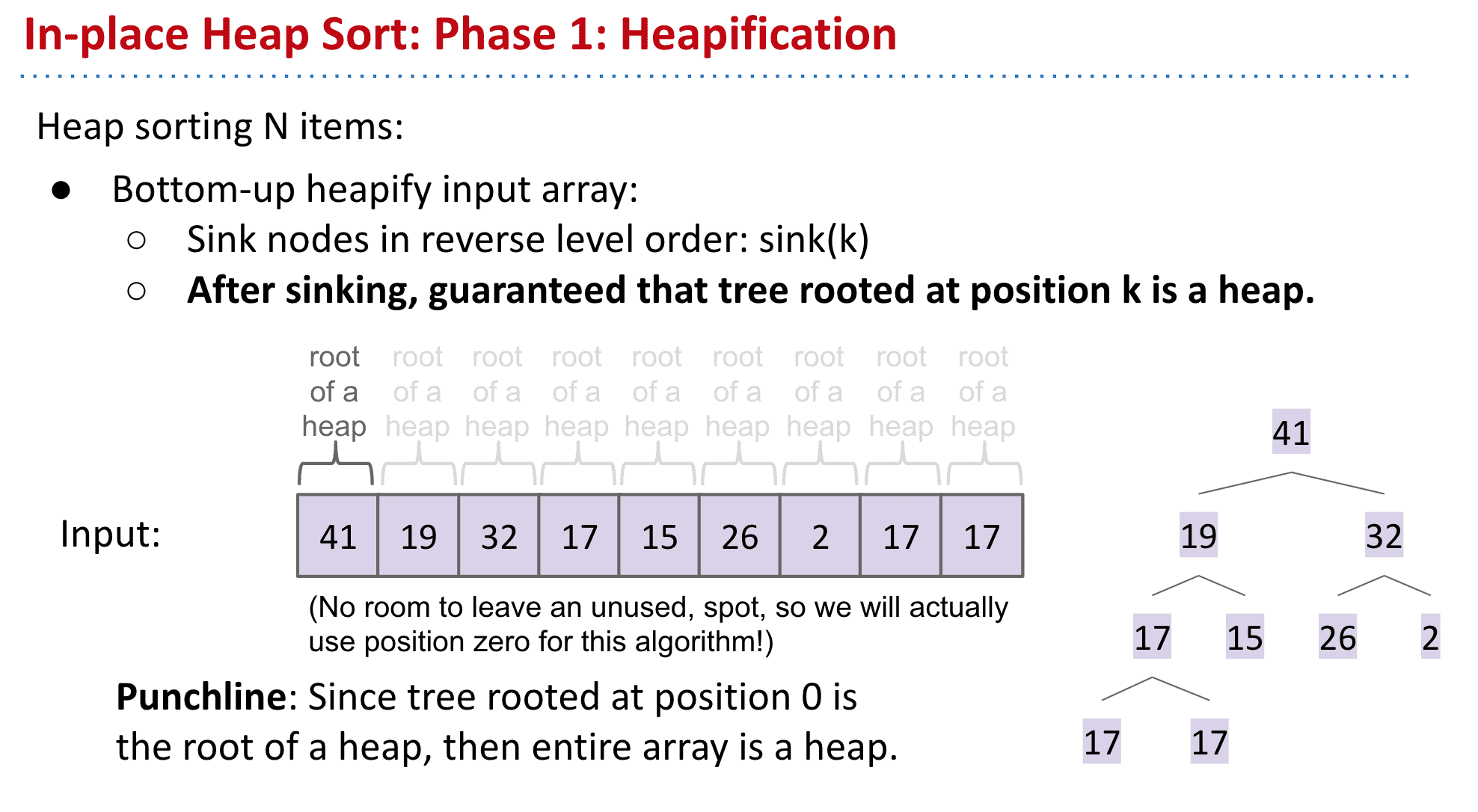
由于这个heap在数组0的位置是一个heap的root,那么整个数组就是一个heap 也就是完成了这个Bottom-up 的操作
和上一个创建一个新数组不一样的是,我们选择就在本身进行操作
首先把root与最后一个交换

然后再次进行上一步的sinking操作得到新的heap+已经固定的root
然后不断重覆将root(第一项)和最后一项替换(heap的最后一项而不是数组的)→sink得到新的heap
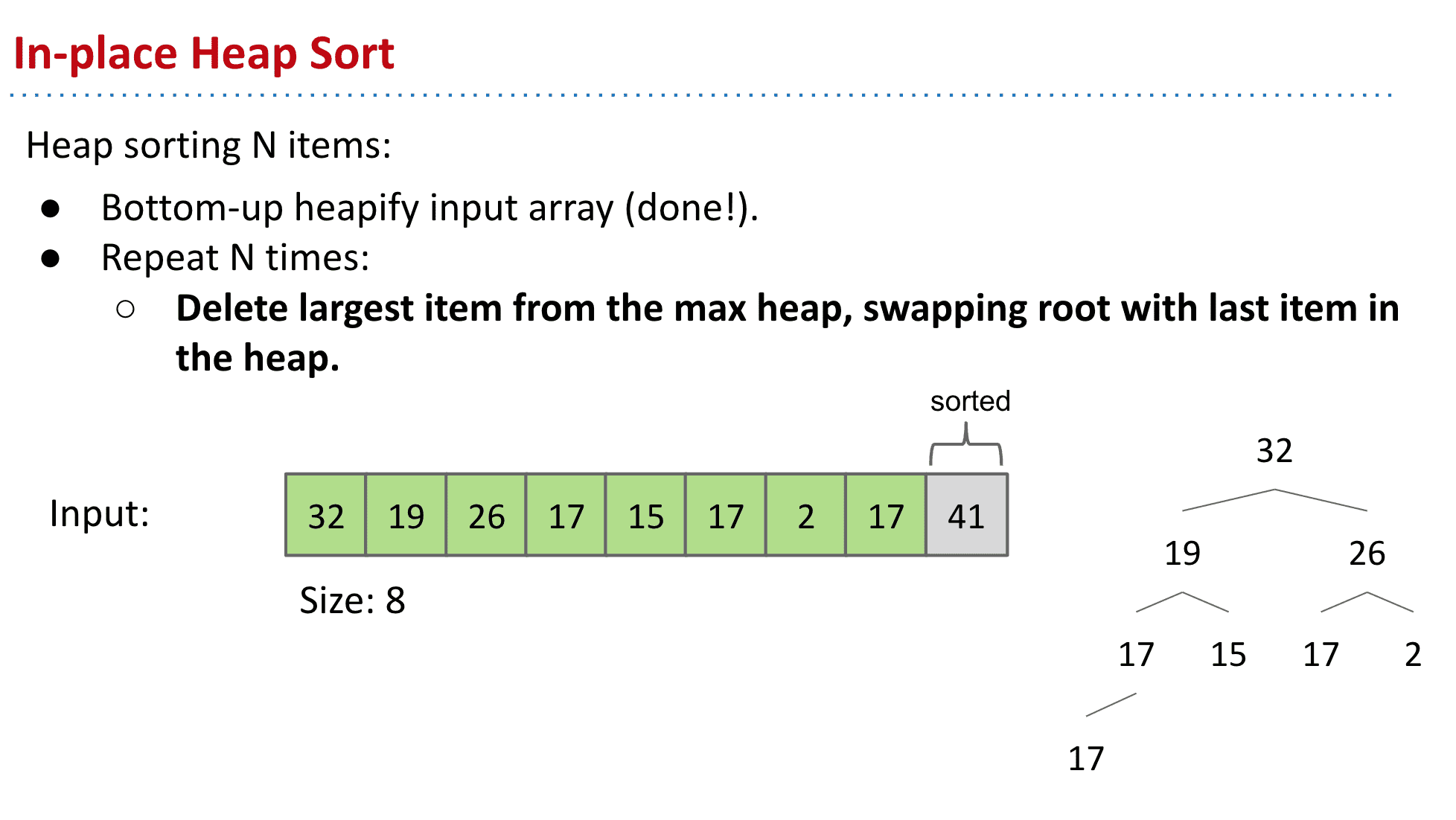
最后就得到了堆排序后的数组
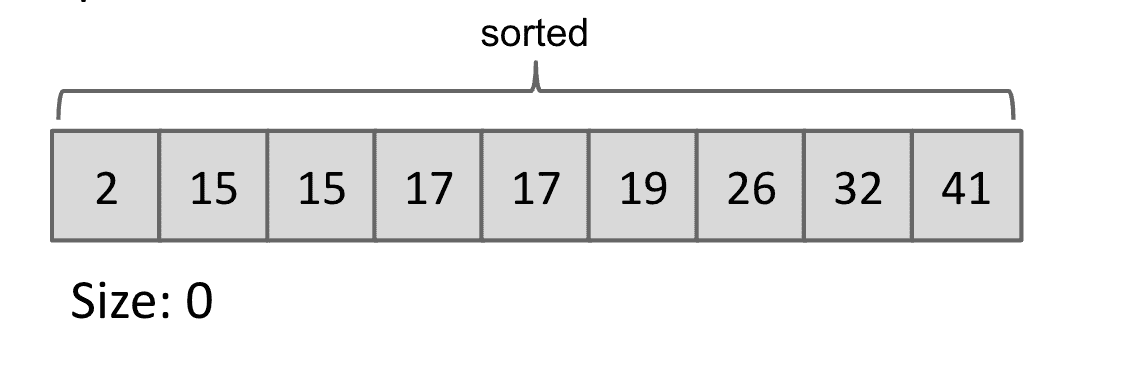
运行时间:
Bottom-up Heapification: O(N log N) time.
Selecting largest item: Θ(1) time.
Removing largest item: O(log N) for each removal.
若以升序排序说明,把数组转换成最大堆(Max-Heap Heap),这是一种满足最大堆性质(Max-Heap Property)的二叉树:对于除了根之外的每个节点i, A[parent(i)] ≥ A[i]。
重复从最大堆取出数值最大的结点(把根结点和最后一个结点交换,把交换后的最后一个结点移出堆),并让残余的堆维持最大堆性质。
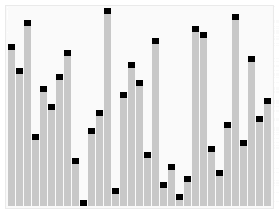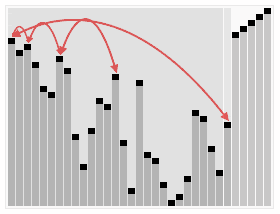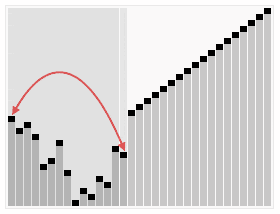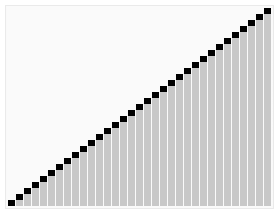
堆排序演示
归并排序 Merge sort:将两个排序合并成一个
同样也是之前学习过的[Mergesort 归并排序]
由于学习过,所以简单介绍一下过程
把items分成2个部分,再分别对他们归并排序(使用了递归 (Recursion),就一分再分)
最终将两个部分里的最大值进行比较,小的就放入新的数组 不断重复直到完成
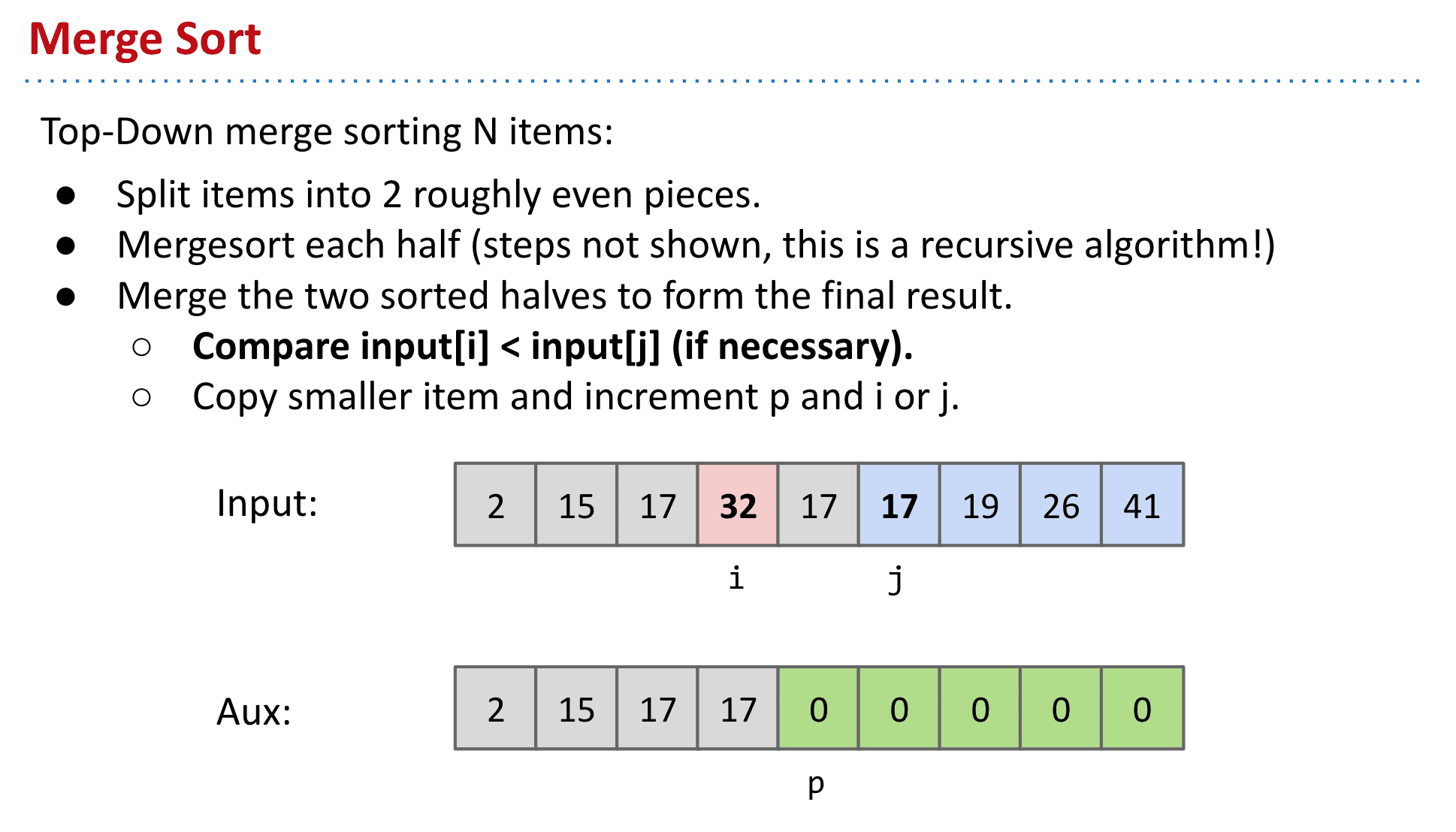
可视化:
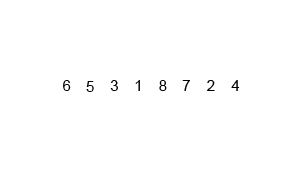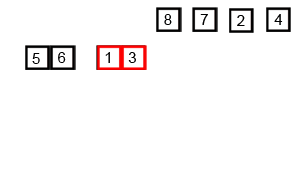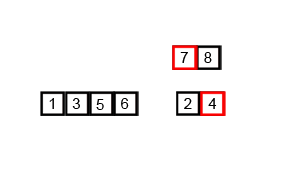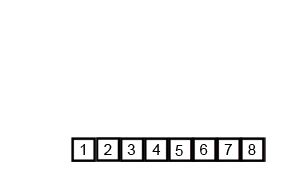
一分再分,再按照大小组合

插入排序 Insertion sort:找到插入item的位置
很简单且低效的排序方式:
把input的item按顺序放入新的数组
如果大就放左边,小就放右边,不大不小就数组在中间找个合适的位置
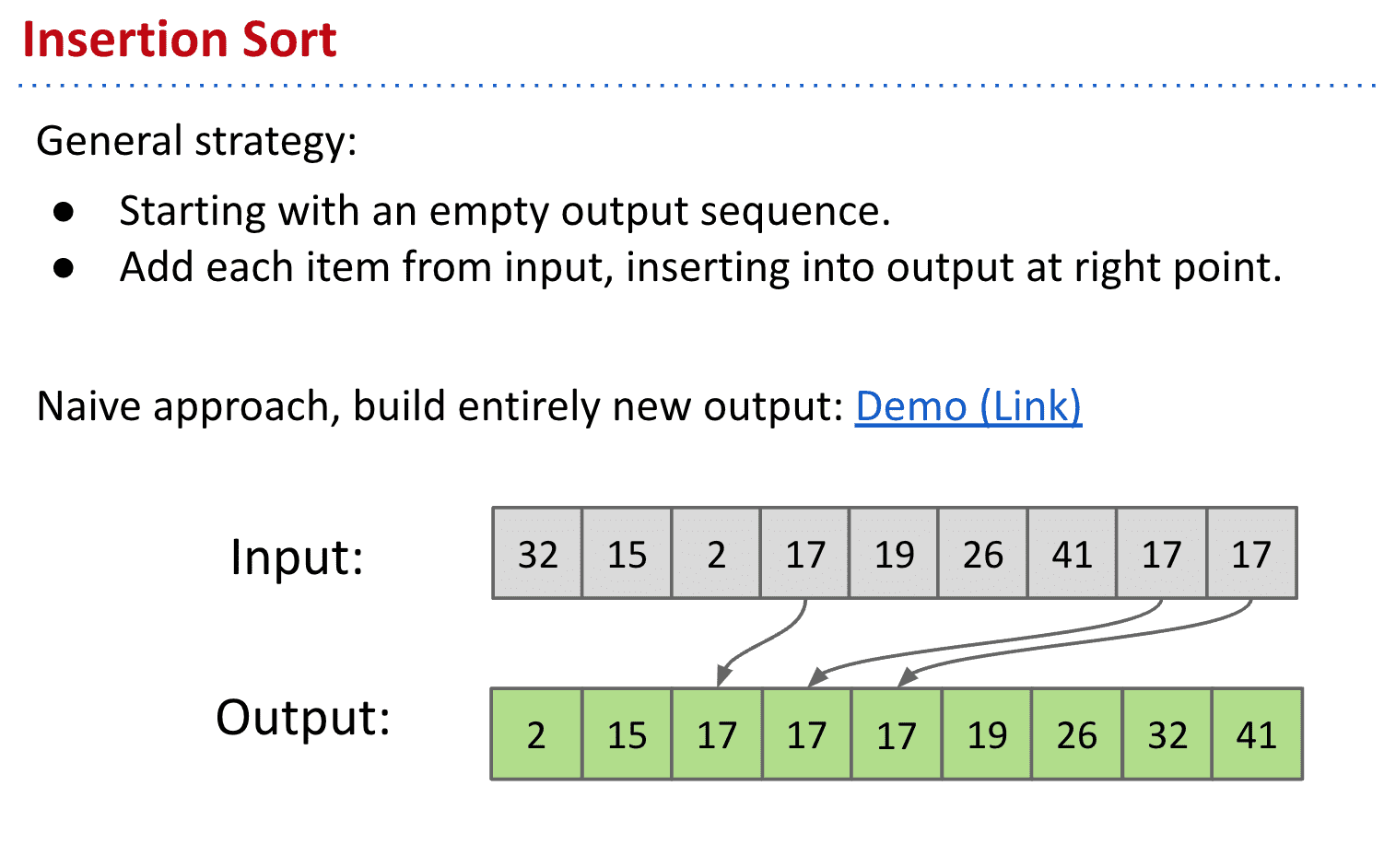
进阶版 使用交换代替插入(in-place)
不另外建立数组,在本身进行交换就行了
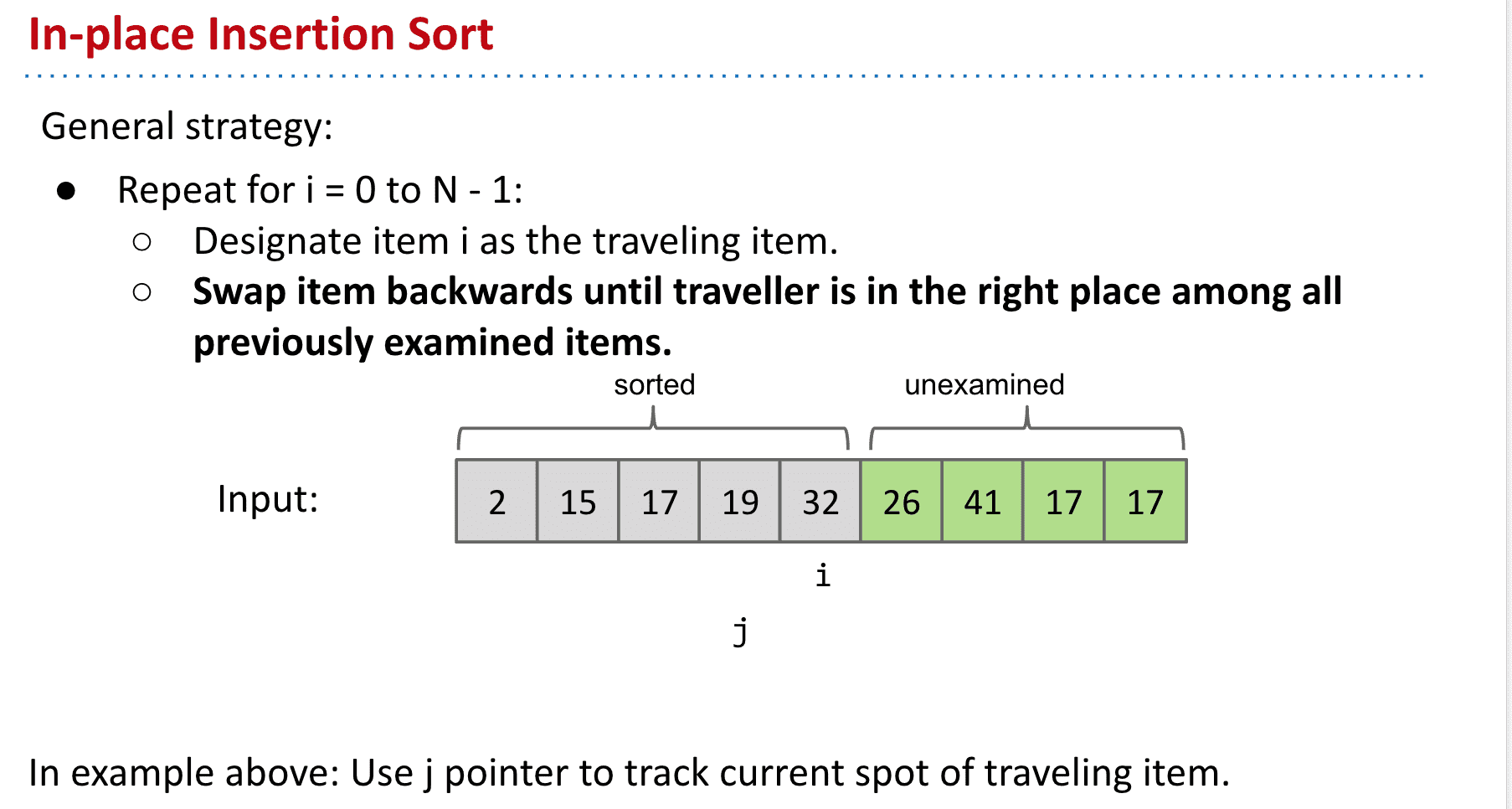

in-place插入排序例子
可视化:
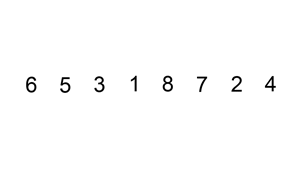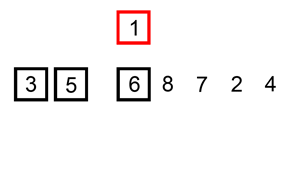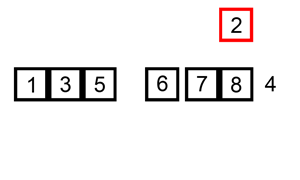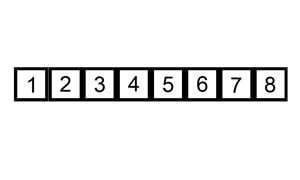

少量反转的数组(也就是几个item位置不对的话)上,使用插入排序非常快
希尔排序 Shellsort :不断分区插入排序
(额外的内容)
大概就是分区进行插入排序,并且随着排序进行,分区越来越小 最终就是普通的插入排序了,只需要移动很小一部分item的位置
例如,假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我们以步长为5开始进行排序,我们可以通过将这列表放在有5列的表中来更好地描述算法,这样他们就应该看起来是这样:
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10然后我们对每列进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45将上述四行数字,依序接在一起时我们得到:[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了,然后再以3为步长进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45排序之后变为:
10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94最后以1步长进行排序(此时就是简单的插入排序了)。
快速排序 Quicksort:把item们分区进行分割(随机性强)
分区(分解) Partitioning
通过将数据分为大于小于某个值来进行分区
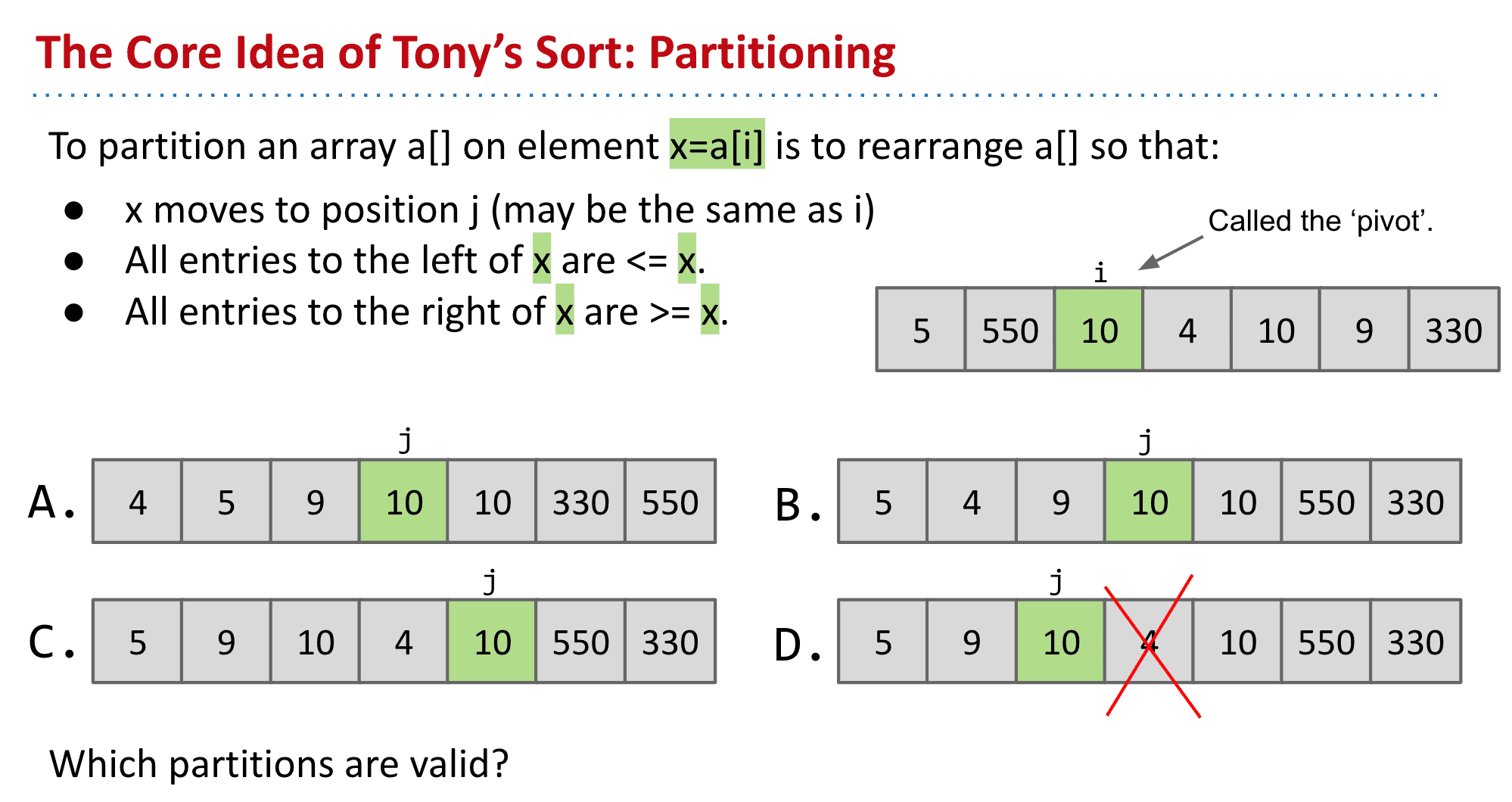
分区有很多种可能的实现方式比如
- 扫描数组然后把红色部分(小于x的)放到x前面蓝色部分不移动
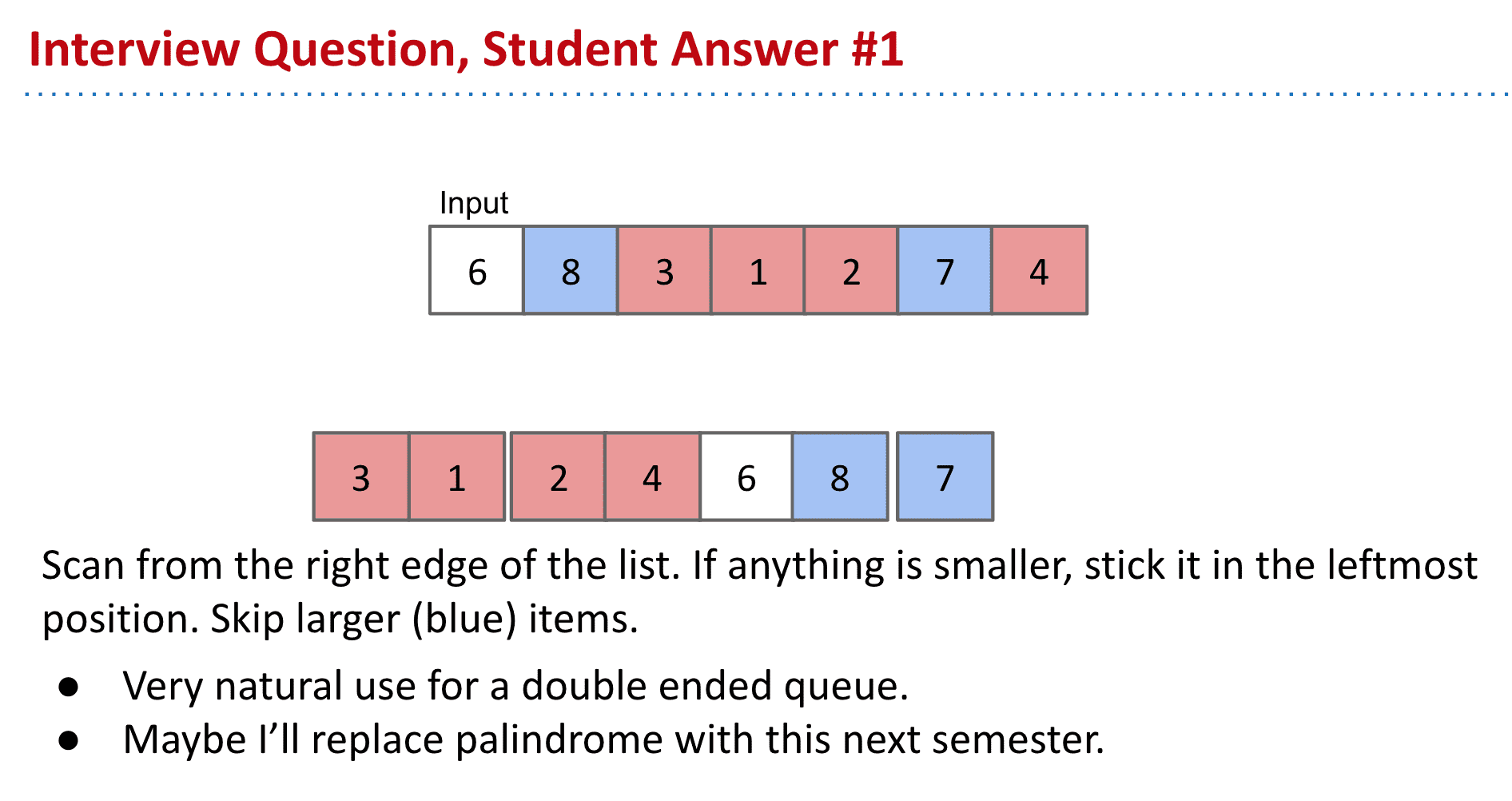
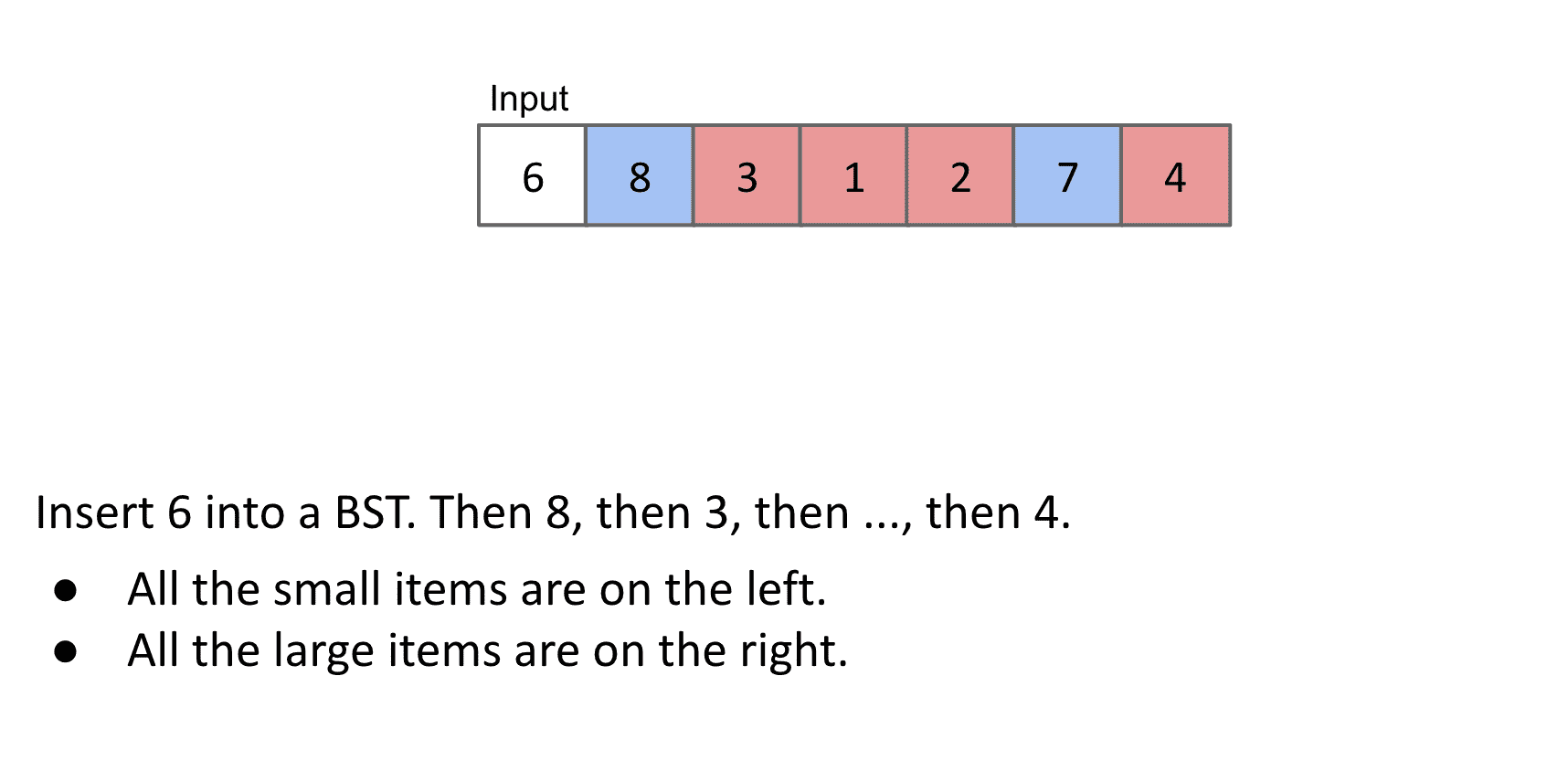
- 使用BST,把数据放到BST中这样root左边的全都是小的右边全都是大的
- 创建一个新的数组然后进行三次扫描
第一次把全部红色的放入新数组
第二次放白色的
第三次放蓝色的
(这种方式不是原作者采用的,但是是本课程采用的方式)

总之有很多种实现分区的方式
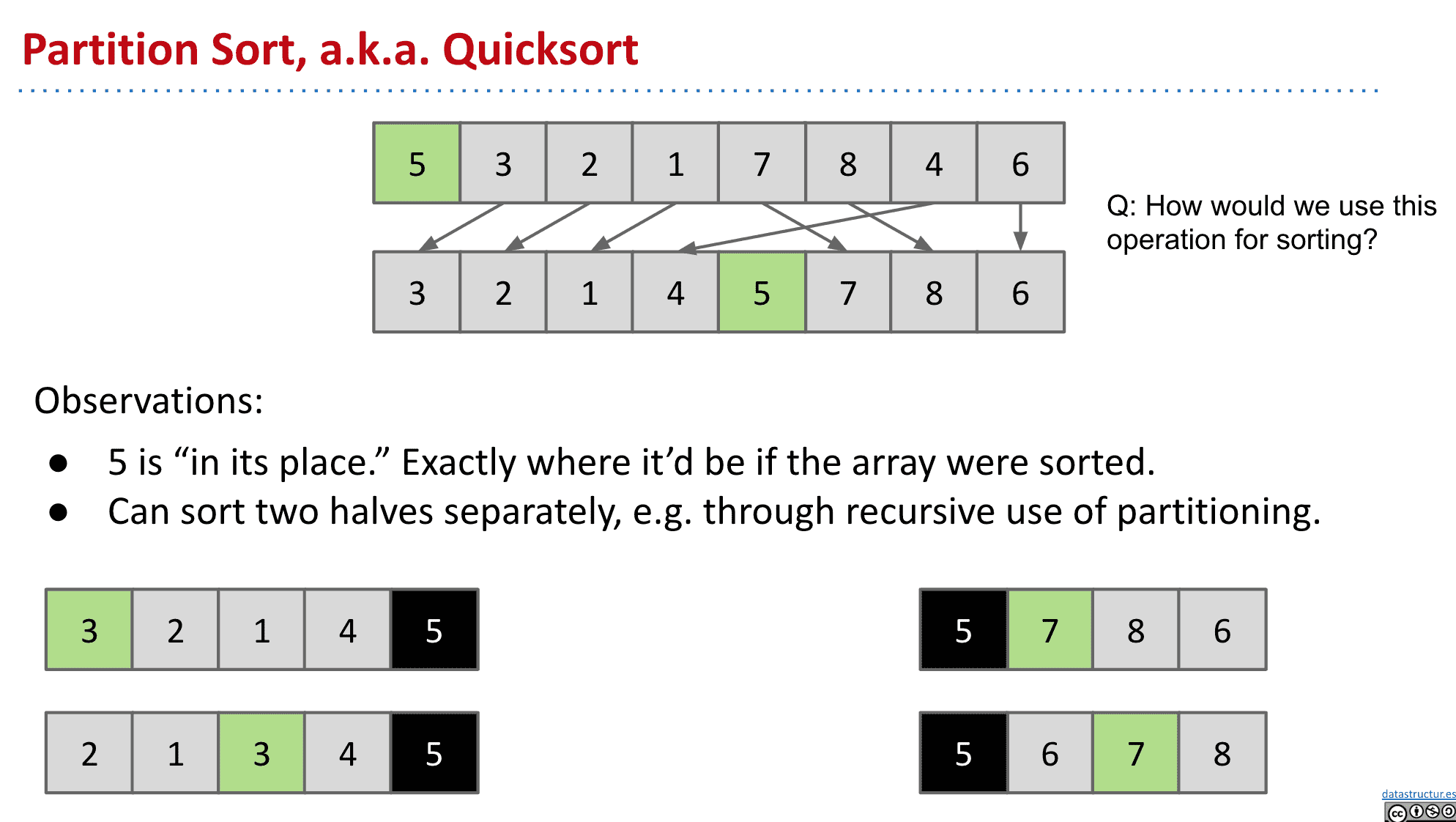
3-scan分区方案
经过分区后(采用上面第三种方法,扫描三次)
可以发现5的位置固定了,因为它左边都是小于5的右边都是大于5的 接下来5没必要再移动位置了
还可以发现左边的区域和右边的区域不需要再相互交流了
‘pivot’也就是绿色点,选区是自由的 但一般选择最左边的点
接下来的部分我们可以继续进行“分区”
每次分区都有一个值被“固定位置”
不断分区后就得到了排序的结果
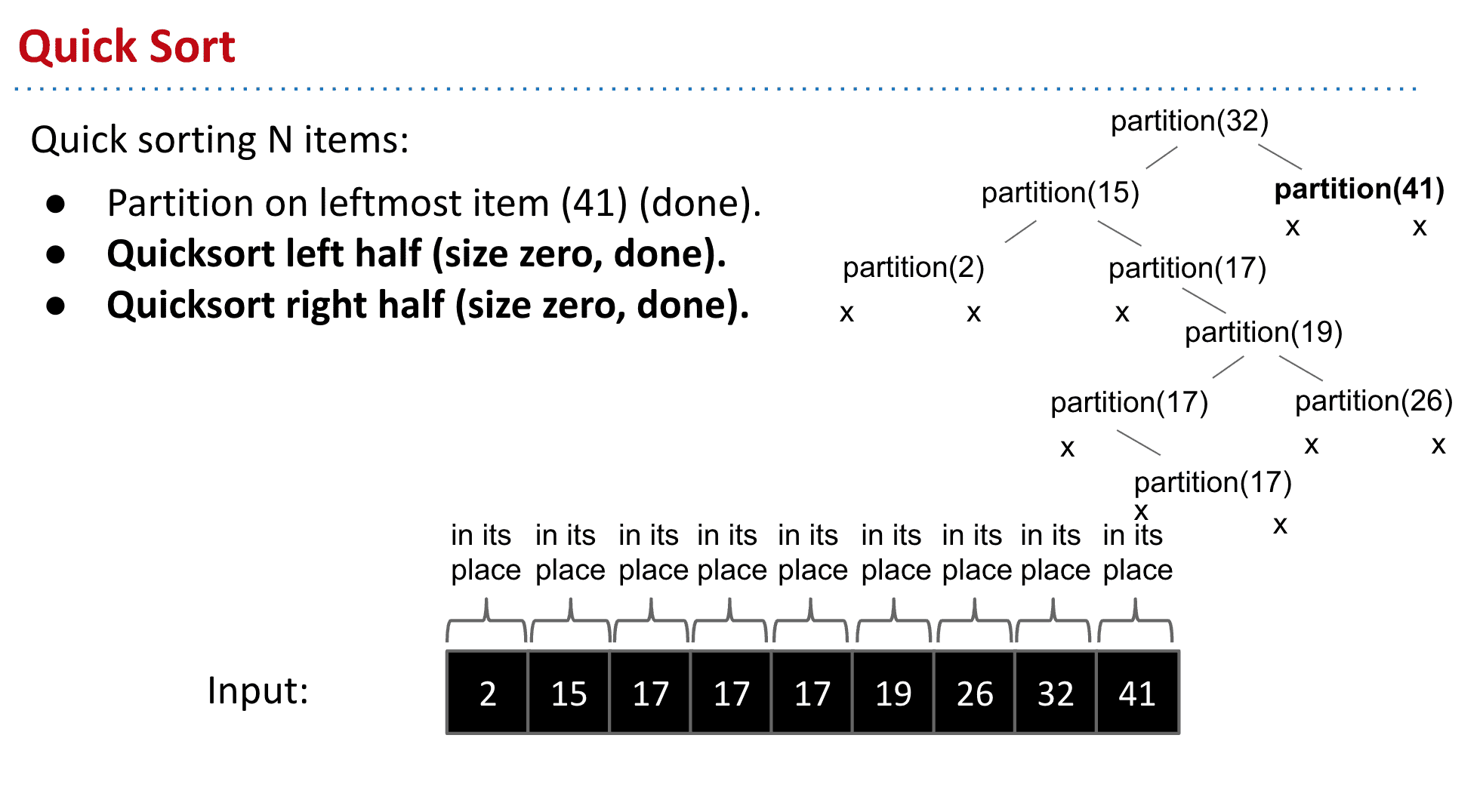
Demo 可以看到这个分区表就有点类似于BST 所有思想其实和方法2差不多
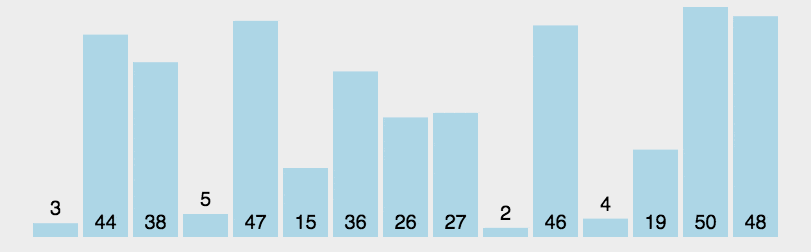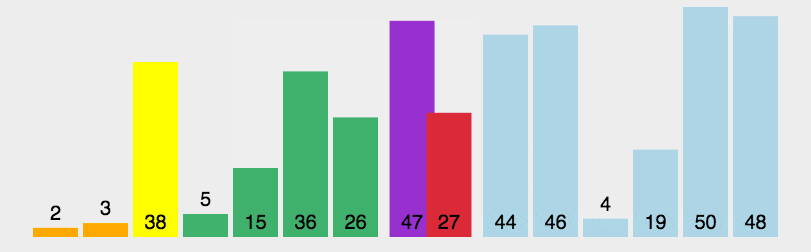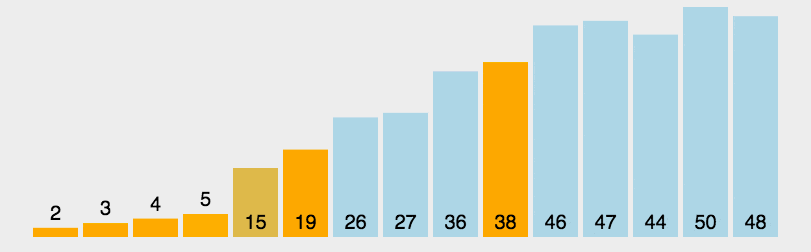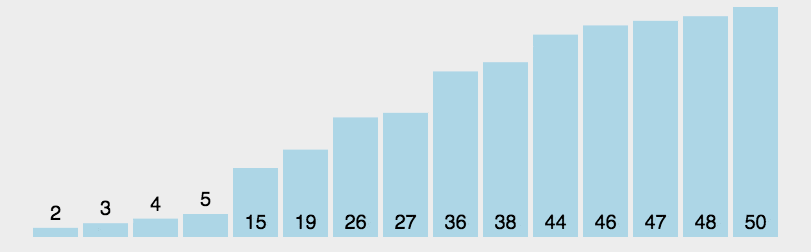
可视化:
在大多数情况下,快速排序都是最快的
快速排序运行时间
哪怕最坏情况比较蛮,但在大部分情况下的平均性能都很好!

快速排序本质和BST排序是一样的
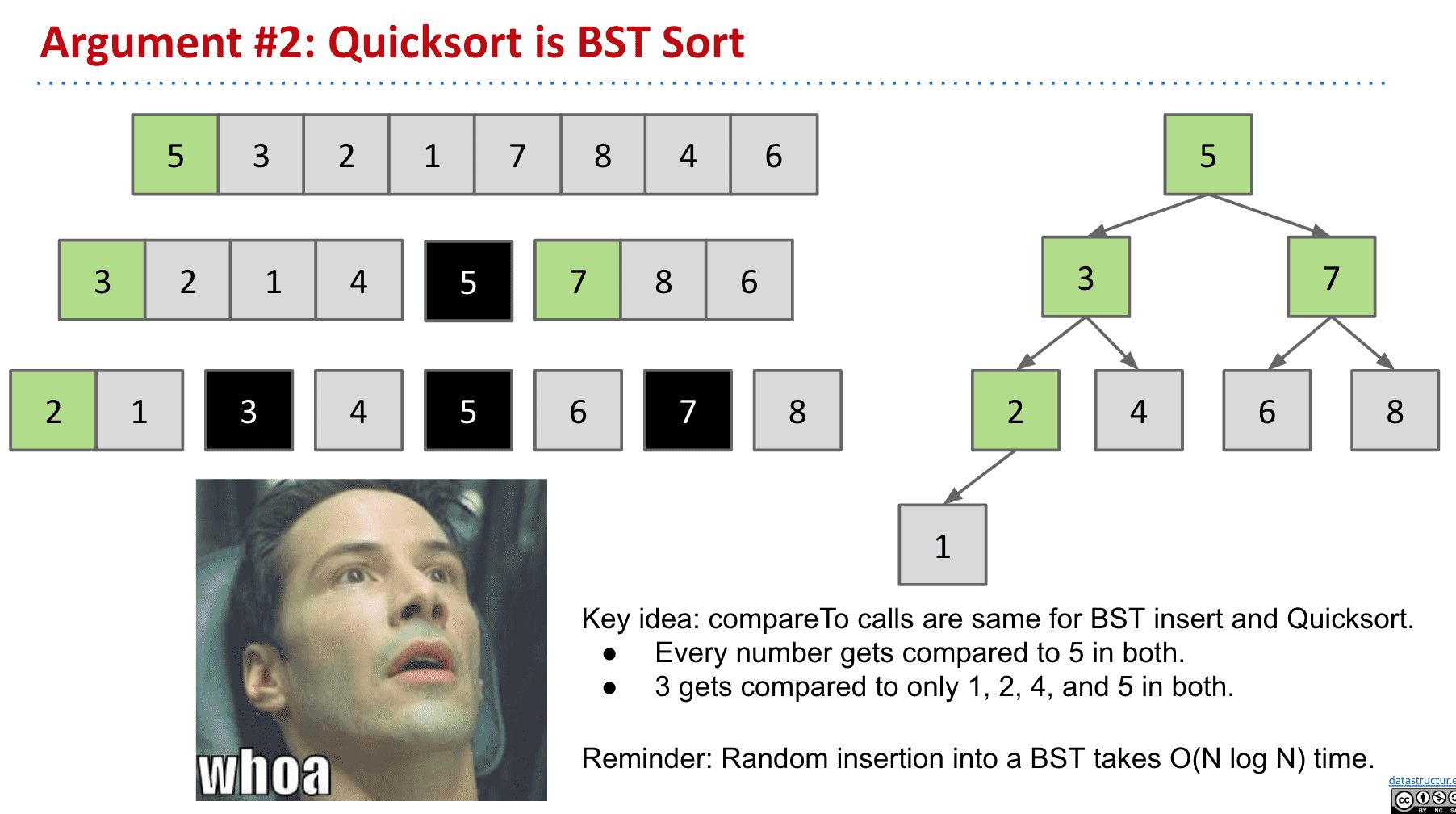
避免快速排序最坏情况产生



避免QuickSort的最坏情况
如果有重复的item或者list已经/接近被排序了这时候使用QuickSort效率就会很低
比如有个list是从大到小排列的,这样每次拿最左边的都会导致需要完全遍历剩下的部分
避免这种情况出现的策略:
- **Randomness:**随机在list里面挑选一个pivot,或者排序前进行打乱
- **Smarter pivot selection:**通过各种算法挑选一个尽量是中位数的pivot(见下面Quick Select)
- **Introspection:**如果递归了很多层就采取其他排序方法(递归多说明效率低可能不适合快速排序)
- **Preprocess the array:**预处理list,比如判断是不是已经/接近被排序的,适不适合使用QuickSort
In-place分区方案
Tony Hoare’s In-place Partitioning Scheme(Demo、参考视频)
与之前一种分区方法对比,不需要额外的内存空间并且快很多 还避免了一些坏情况
基本想法是选择一个pivot(可以随机选择)然后一个左和右指针,左指针喜欢比pivot小的值,右指针喜欢比pivot大的值
两个指针都向着对方前进,遇到不喜欢的值后停下来,都停下来后就交换不喜欢的值
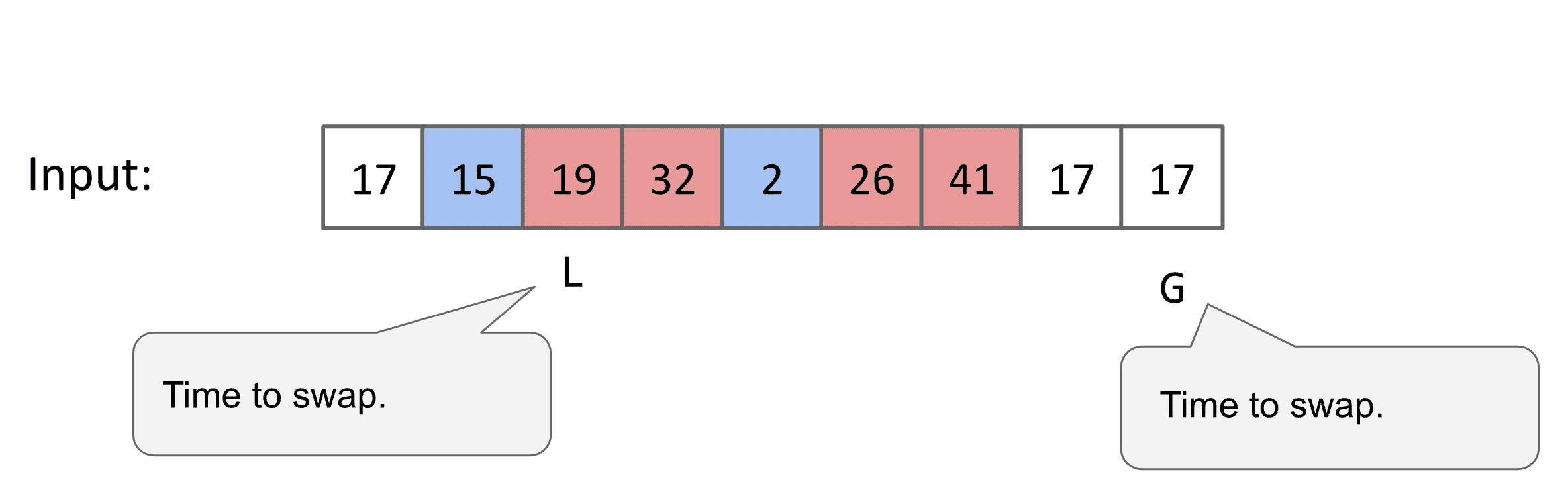
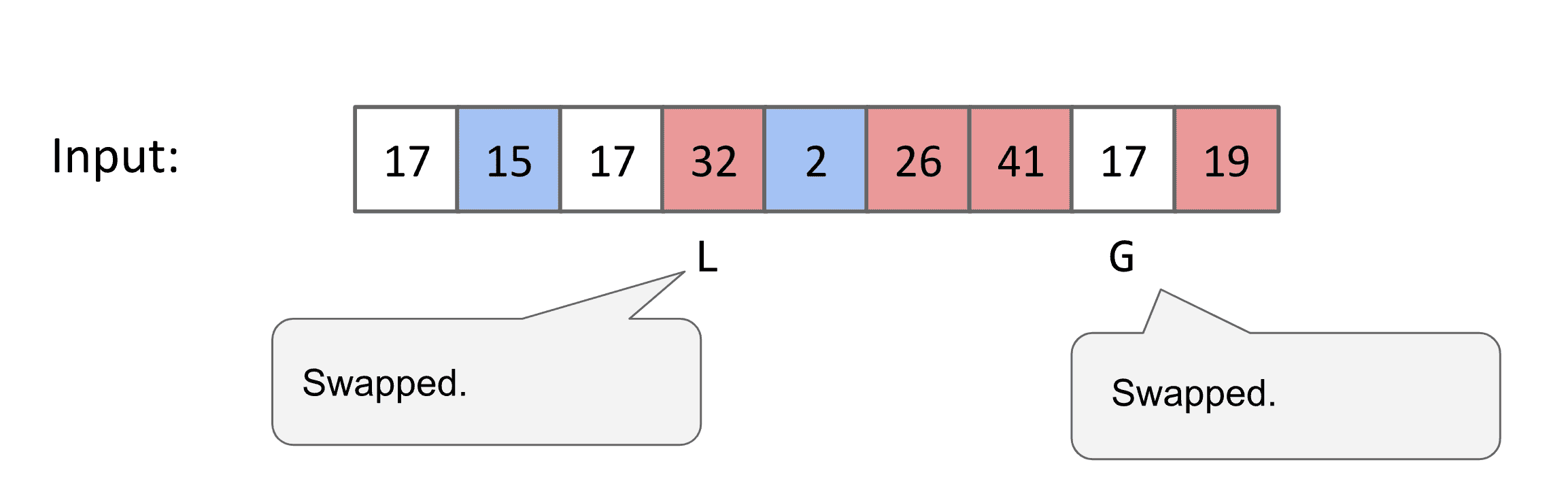
两个指针穿过后就不再前进了,这时候需要选新的pivot
最终左边都是比较小的值右边都是比较大的值
可以看到这种双指针的快速排序速度最快
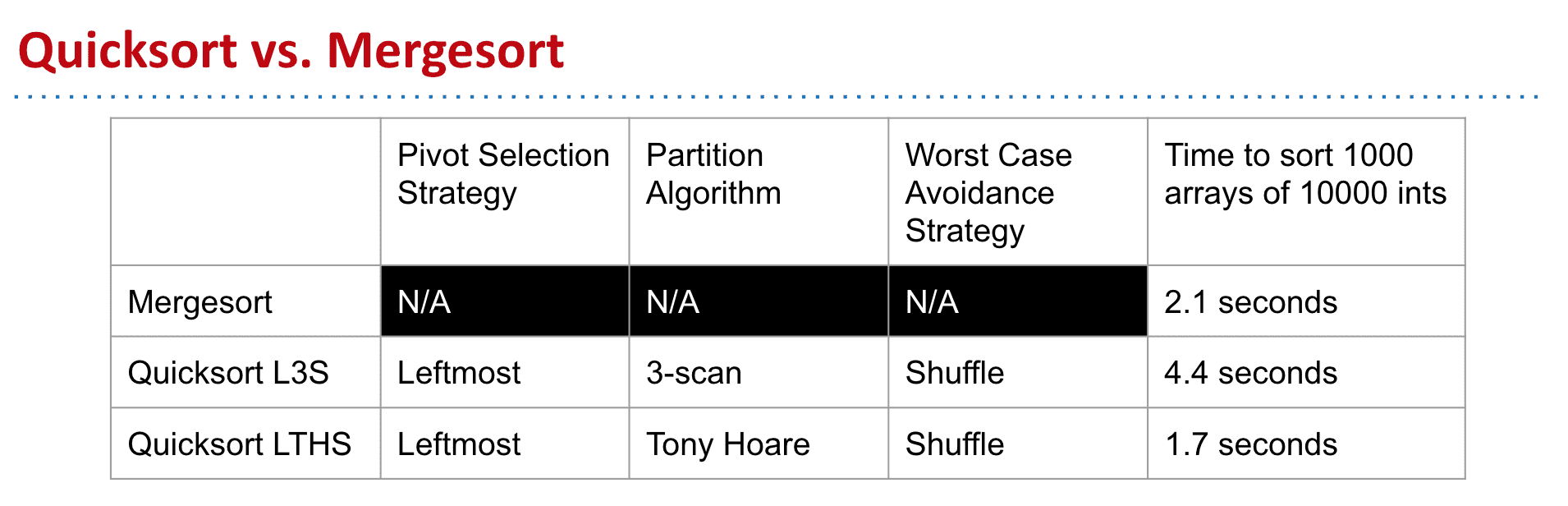
均是未优化版本.对于小的数组没有切换到插入式排序
另外最快最流行的分区方案是:two-pivot scheme
Quick Select
寻找精确的中位数需要耗费大量时间,但分区其实可以帮助我们(这也是最常用的寻找中位数算法)

其他排序相关
稳定性 Stability
**排序算法稳定性:**假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
例子:先按照名字排序再按照年级排序,有稳定性的就能保持之前的顺序,而没有稳定性的就会互相穿过

有稳定性的算法

无稳定性的算法
N log N = log N! (渐近上)
证明:video



总结:只要使用了比较的排序方法runtime Ω(N log N)

最少排序数
对 n 个元素进行排序所需的最少比较次数:0、1、3、5、7、10、13、16、19、22、26、30、34、38、42
(比如3个元素最少比较3次,4个最少五次)
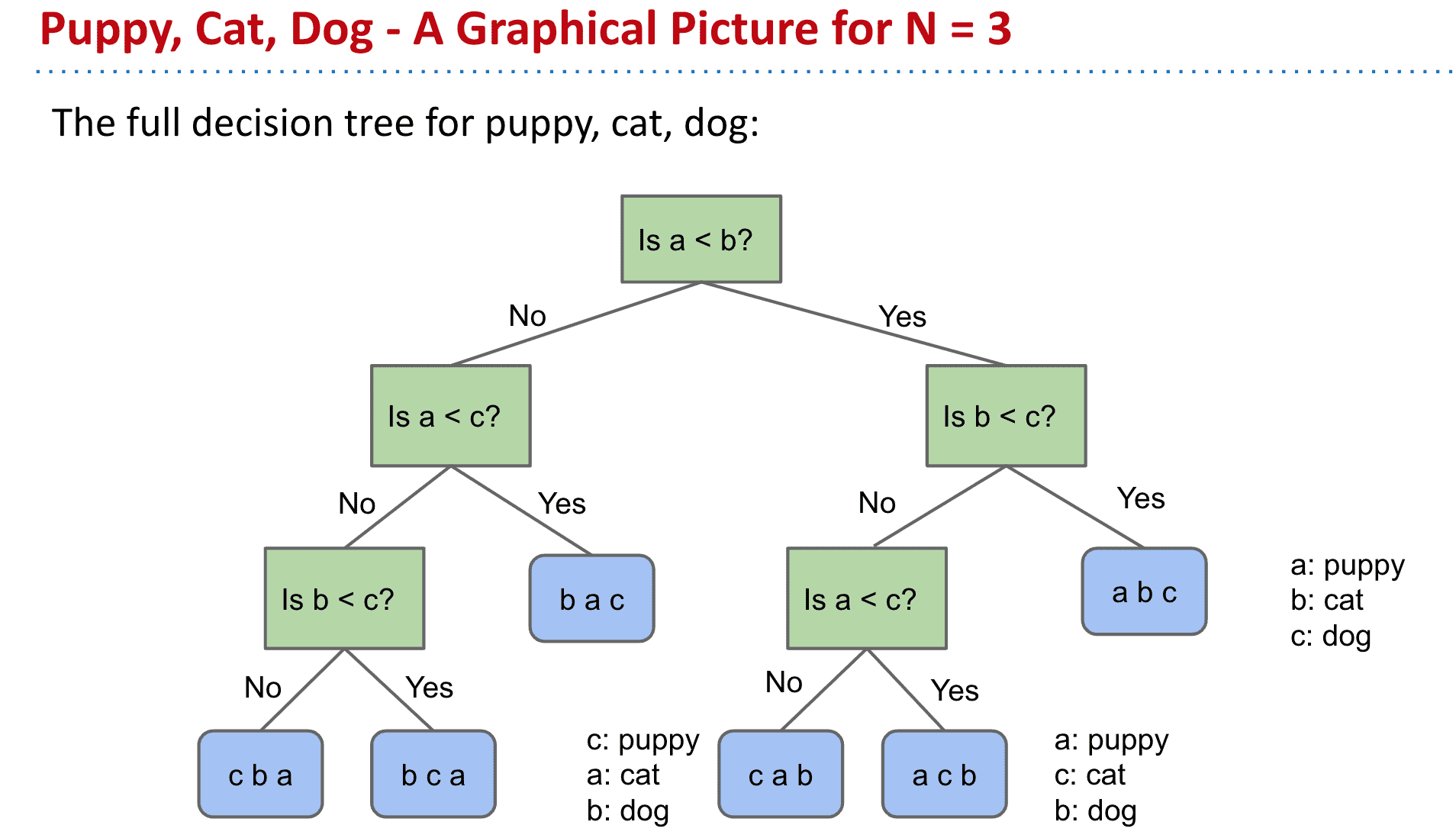
3个元素需要问3次
排序可视化
15 Sorting Algorithms in 6 Minutes
软件工程 Part 2
软件工程(1/3):[软件工程 Software Engineering I]
复杂性是与软件系统的结构有关的任何东西,它使人难以理解和修改系统
比如这样一段代码,有大量重复内容,有很多low level的细节,如果有错误修改起来很困难/麻烦
条件也很长并且没有注释帮助理解代码作用
扩展性不强,如果有新的条件就又需要添加
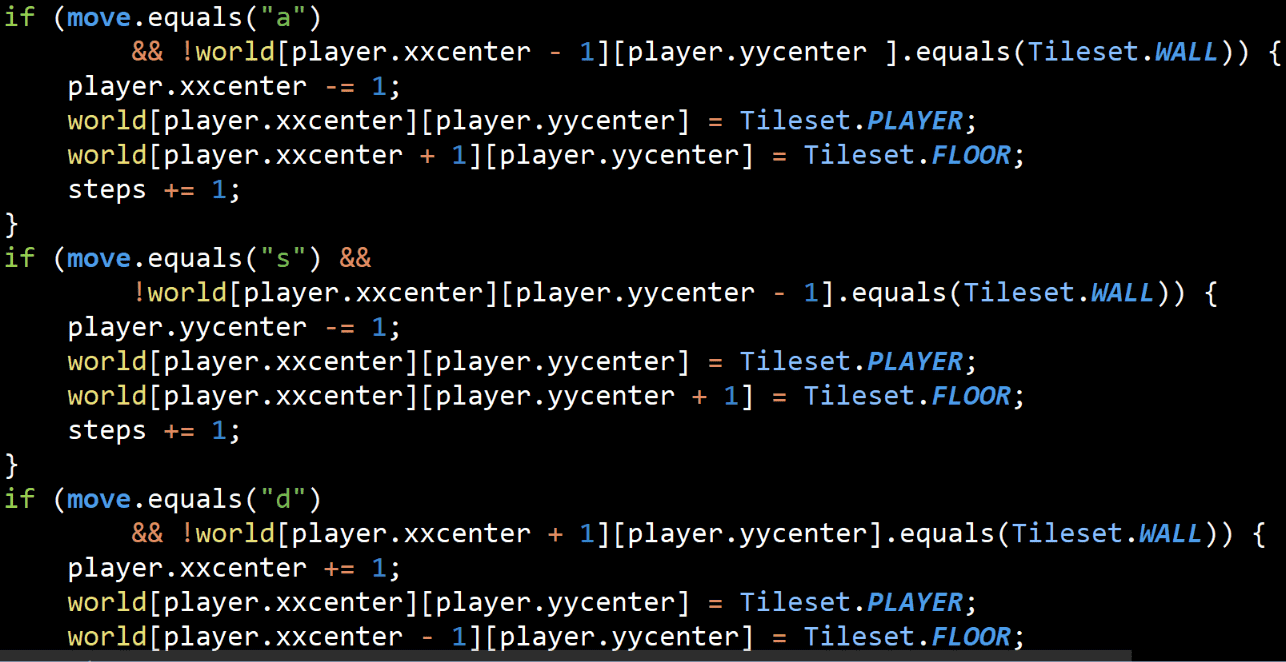
写出各种helper函数比如occupied(WEST, here)就能去掉很多重复代码和方便修改
复杂性有两个主要来源
依赖性:当一段代码不能被独立阅读、理解和修改时(比如上面很长的条件,到处重复的PLAYER)
隐蔽性:当重要信息不明显时(不能一眼看出在做什么,重复的代码,魔力数字等)
模块化设计 Modular Design
我们应该依靠模块化来隐藏复杂度,比如使用helper函数等
在一个理想的世界里,系统会被分解成模块,每个模块都是完全独立的。
这里,"模块 "是一个非正式的术语,指的是一个类、一个包或其他代码单元。
模块不可能完全独立,因为每个模块的代码都要调用其他模块。
例如,需要知道方法的参数来调用它们。
在模块化设计中,我们的目标是尽量减少模块之间的依赖关系。
比如接口和实现(Interface vs. Implementation)
就是一个隐藏复杂度的方法
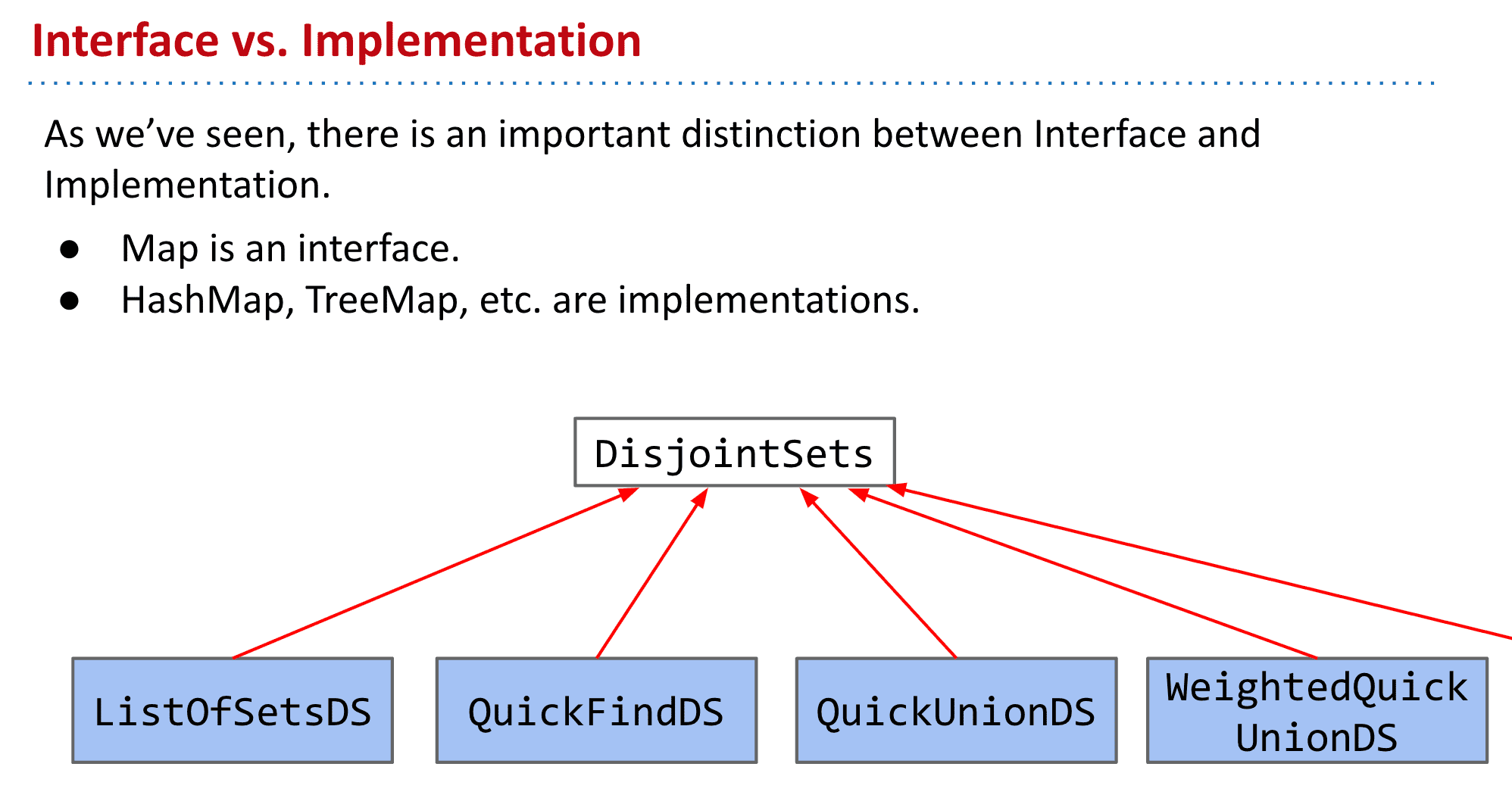
一个简单的接口可以将模块在其他地方造成的复杂性降到最低。如果你只有一个getNext()方法,那就是别人能做的全部。
如果一个模块的接口很简单,我们就可以改变该模块的实现而不影响接口
(比如List如果只有个arraysize方法而不是size方法,就限制了我们只能做ArrayList 所有接口要尽可能简单)
"最好的模块是那些提供强大功能而又有简单界面的模块。我用深度这个词来描述这种模块"。
例如,RedBlackBSTSet 2b就是一个深度模块。
简单的接口:添加、包含、删除方法,没有任何用户需要知道的非正式的东西(例如,用户不需要指定或知道哪些节点是红色或黑色的)。
强大的功能:操作是有效的,使用复杂、微妙的规则维持树的平衡
用户只需要知道有这个功能而不必在意下面复杂的实现
就和以前学习计算机体系一样,每次封装、抽象都有利于我们接下来更加方便的建造新的东西,如果在写一个CPU的HDL时还要考虑nand门的话 就太复杂了,二进制机器码→汇编→高级语言 这一过程就是通过封装来减少复杂度 所以我们才能写i++而不是0110101001111…之类的东西
避免过度依赖 "时间分解(temporal decomposition)",在这种情况下,代码按照现实发生的顺序进行,这样在进行其他操作时就很容易出问题 (比如应该使用一个统一的类来管理输入,而不是按照现实顺序觉得应该输入了,导致有多个入口)
使用一些时间上的分解是可以的,但要设法修复任何发生的信息泄漏
软件工程 Part 3
这一部分hug没有讲课程
而是关于个人生活职业发展还有科技产品夺走我们注意力的一些事
看完了还感慨蛮多,比如有人认为什么在线课程会让学历价值稀释(我也有这种黑暗想法,哪怕我是受益者2333)
在伯克利学习的这些东西会成为大型企业需要的(但我现在还不确定能不能找到工作,以后人生该怎么办)
人们的焦虑,关于回复社交网络讯息之类的
总之我觉得学习一定不是坏事,希望能做到WLB和终身学习
有这么多高质量的课程可以学习真的很幸运,哪怕没有伯克利或者其他名校的学历
但是课程带来的价值依然很巨大(没有同学关系网、学历背书、课程讨论会差很多就是)
总之我想我应该花更多时间在个人提升上,而不是meanning less的时间消耗产品上
很少在笔记里写这些可能更属于日记的东西,但就像这节特殊的课程一样 也行我需要更多的思考吧
基数排序 Radix sort
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串和特定格式的浮点数,所以基数排序也不是只能使用于整数。
正如之前所说的,只要使用“比较”来排序最坏情况都是N log N,如果不比较的话是不是就能有更好的算法了呢
Sleep Sort (for Sorting Integers) (not actually good)
基本思想就是按时间把元素打印出来来排序(实际这种性能还是很大,不现实)

Counting Sort: Exploiting Space Instead of Time
前面的数字类似于index,我们新建一个数组直接放进相应的位置就可以了,不用进行比较
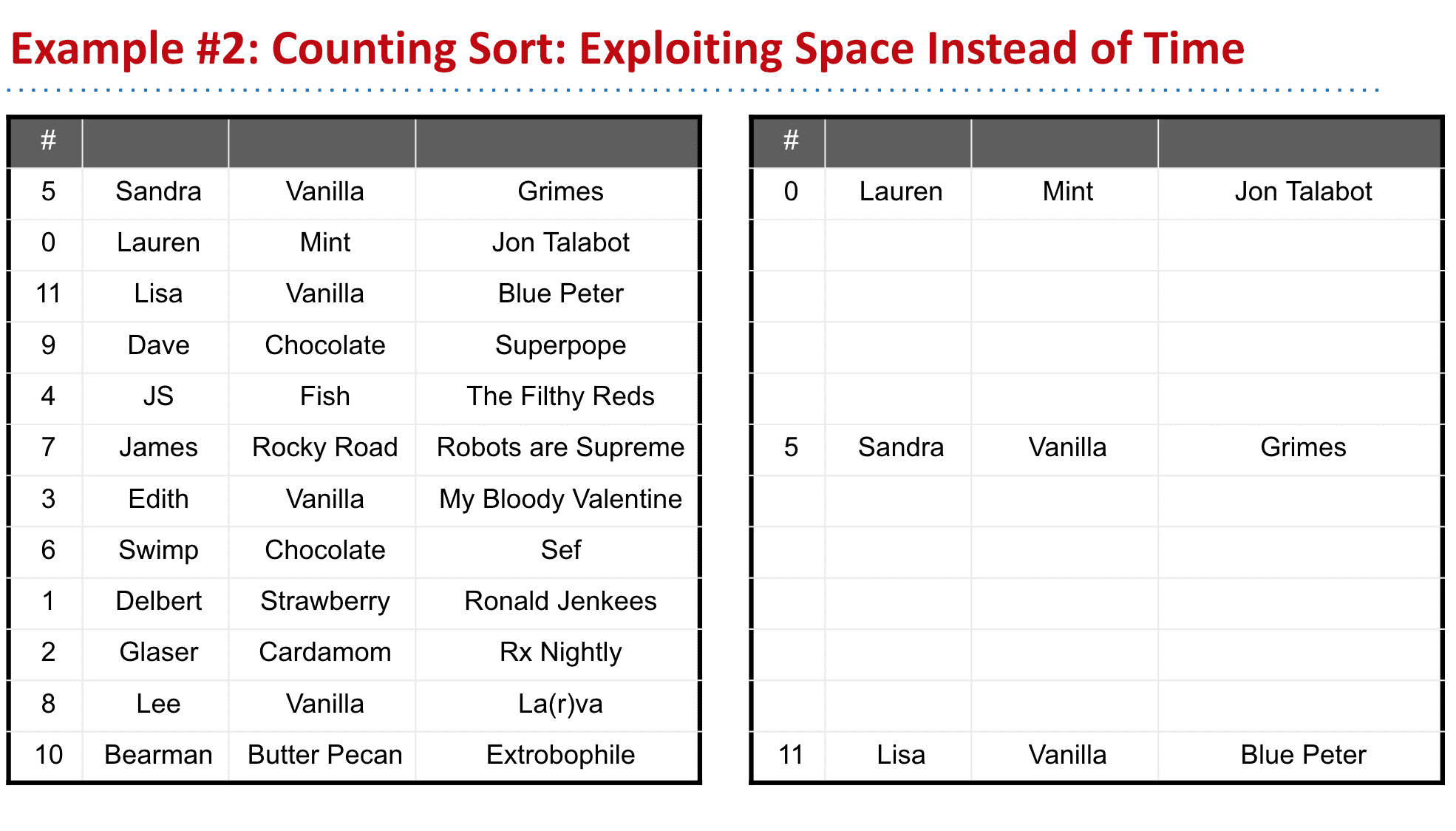
如果有不是数字或者唯一的index,我们就可以计算重复次数再生成新的数组
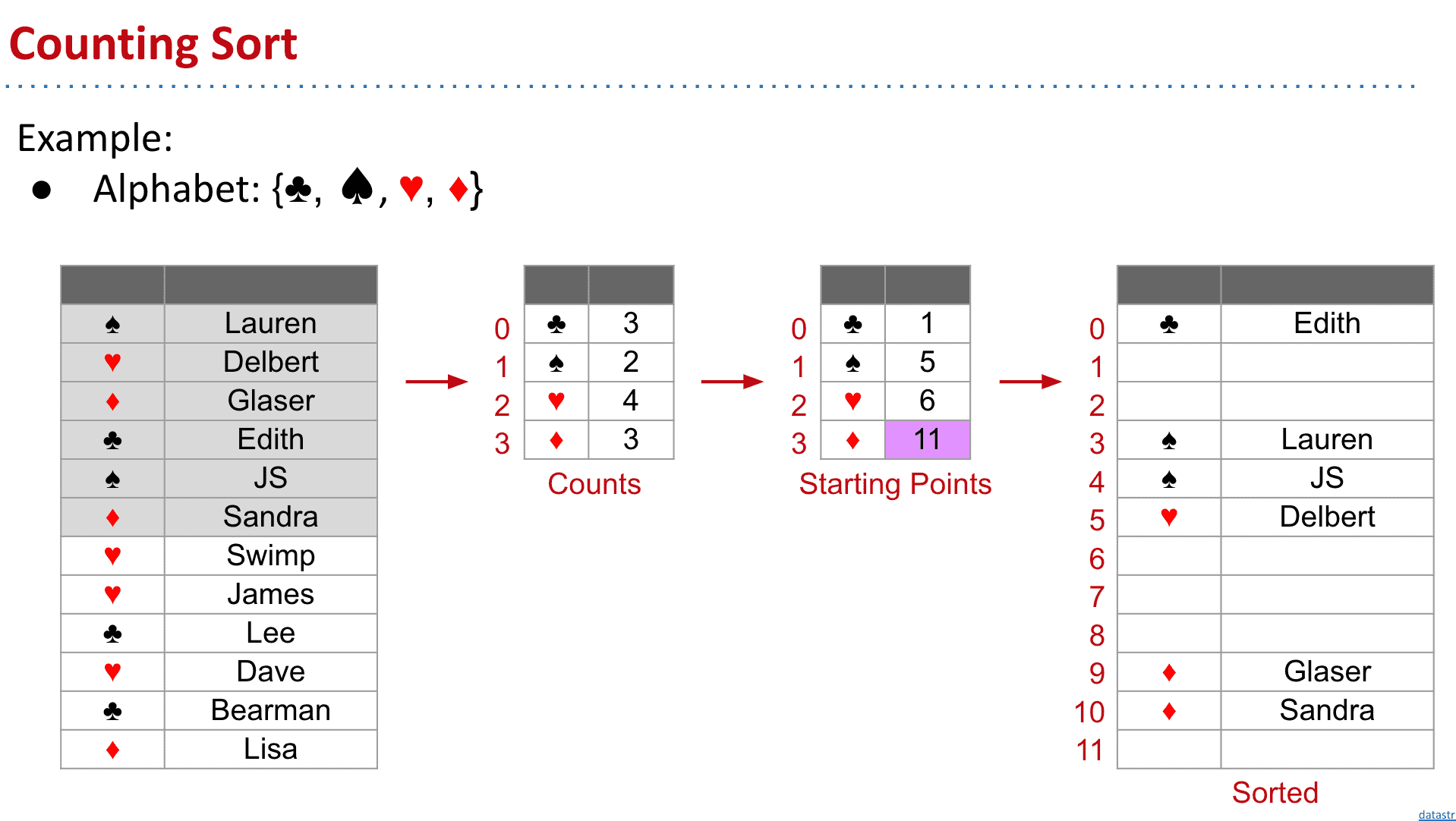
如果计算世界人口最多的100个城市Quicksort比Counting Sort好,因为我们可能要创建一个几百万的数组来放这些城市
Runtime:

LSD Radix Sort
非常早的一种排序方式
先从最右边一位开始排序直到最左边的,这种顺序也能保障最终的排序是对的
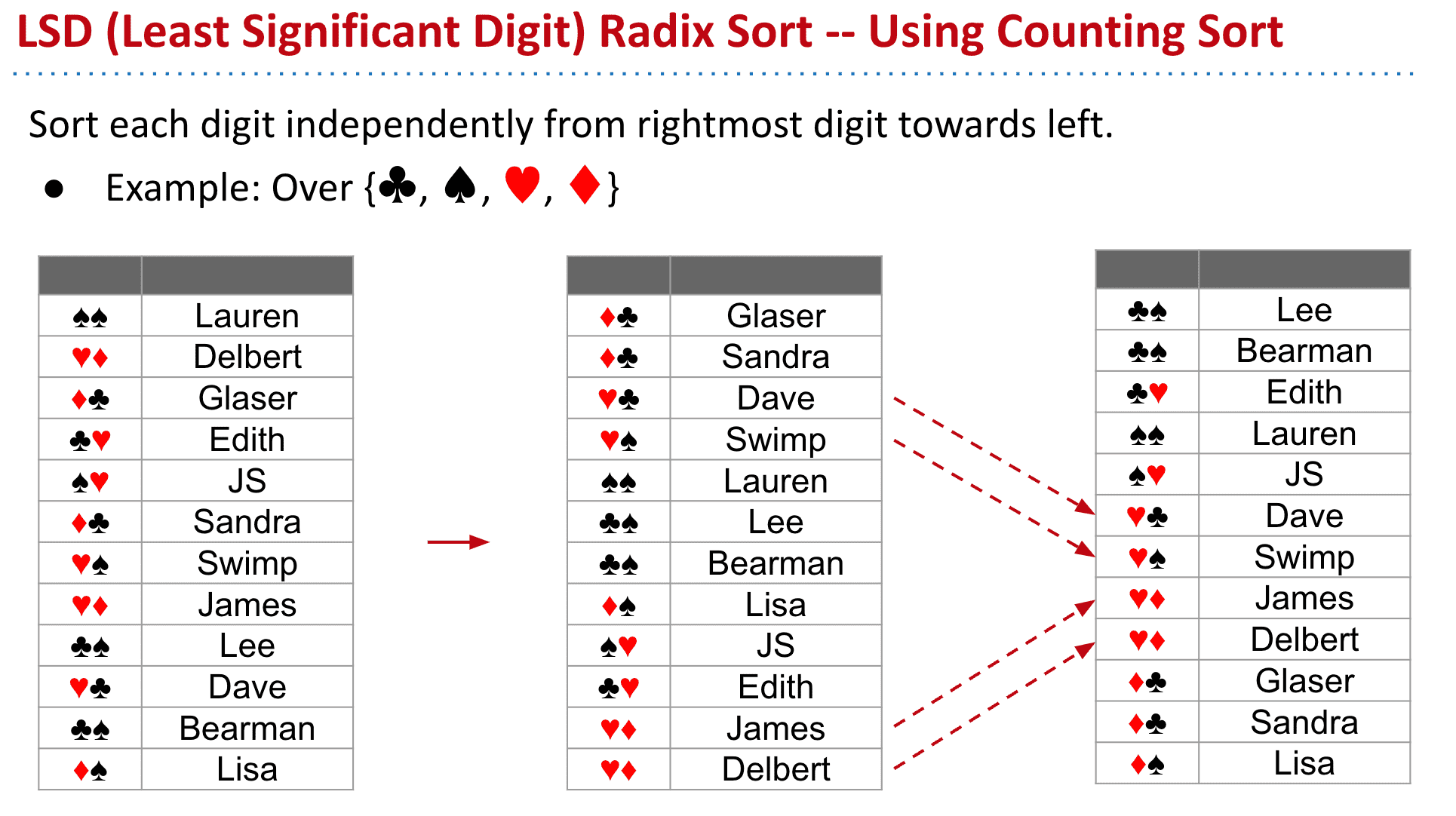

如果key是位数不同的,可以把空的地方看作一个比其他key都小的空白
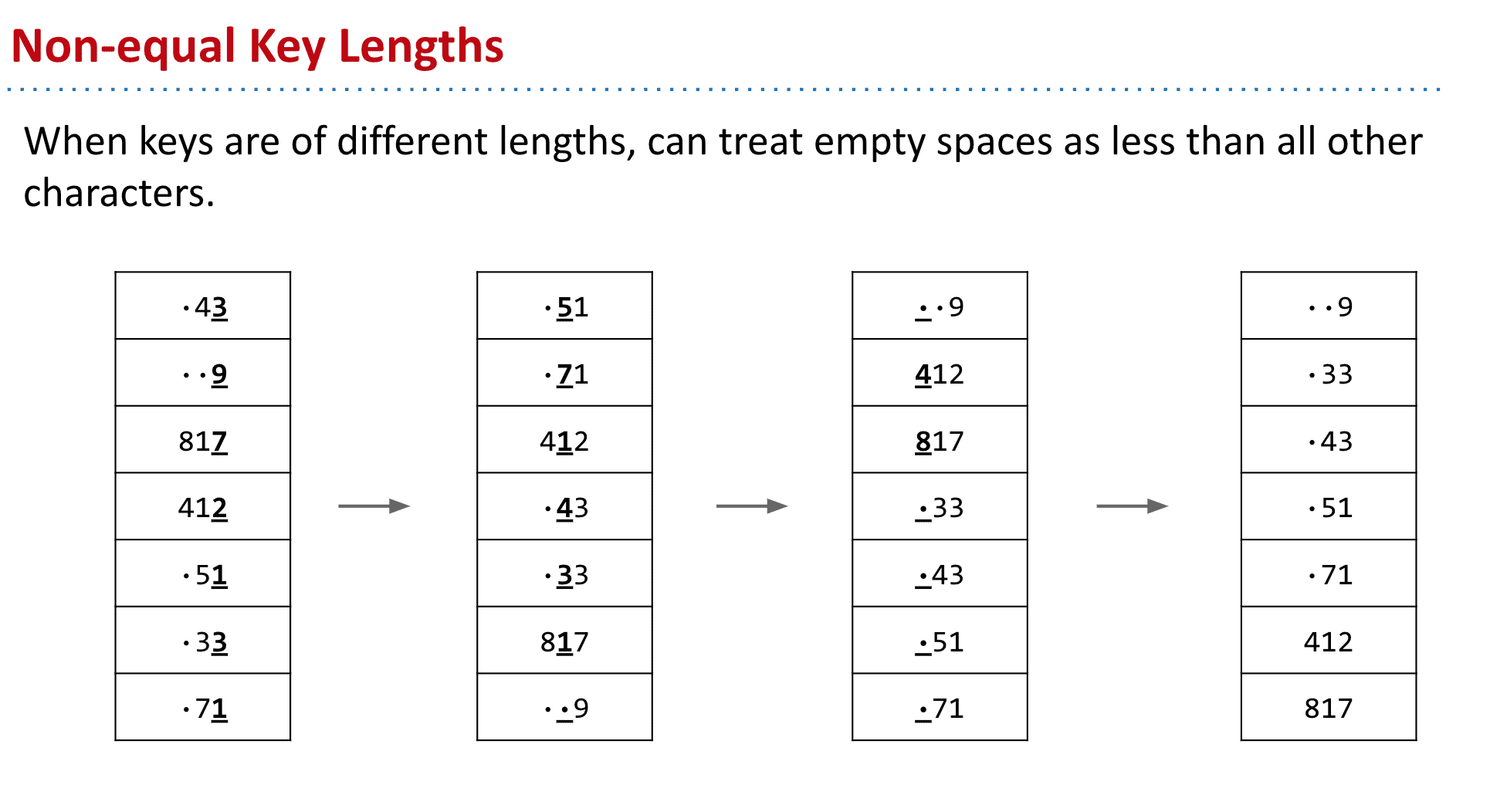
MSD Radix Sort
虽然是LSD翻着来,但是会出现如下问题:再次按位排后会错乱
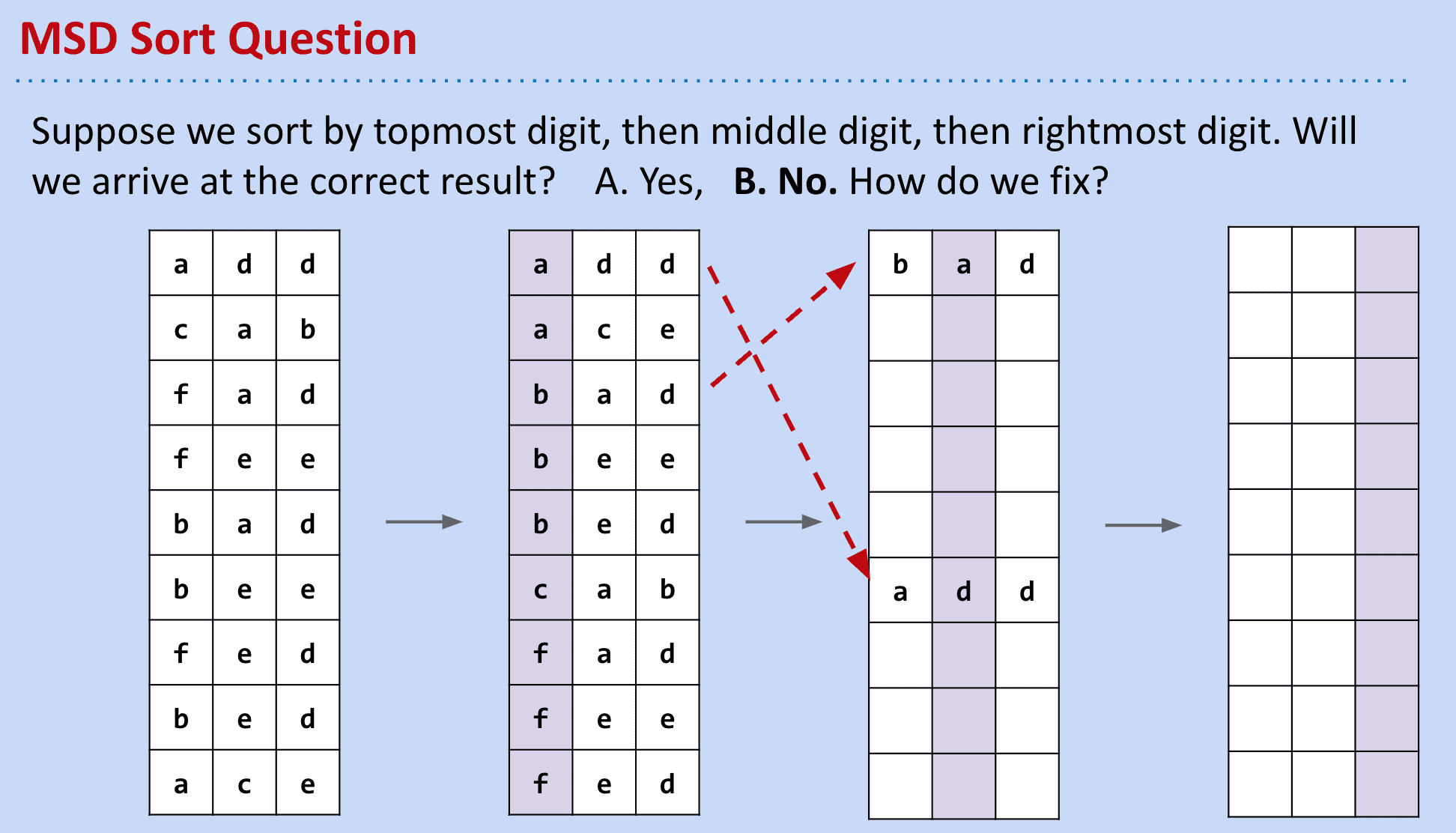
所以我们可以当成子集来对待
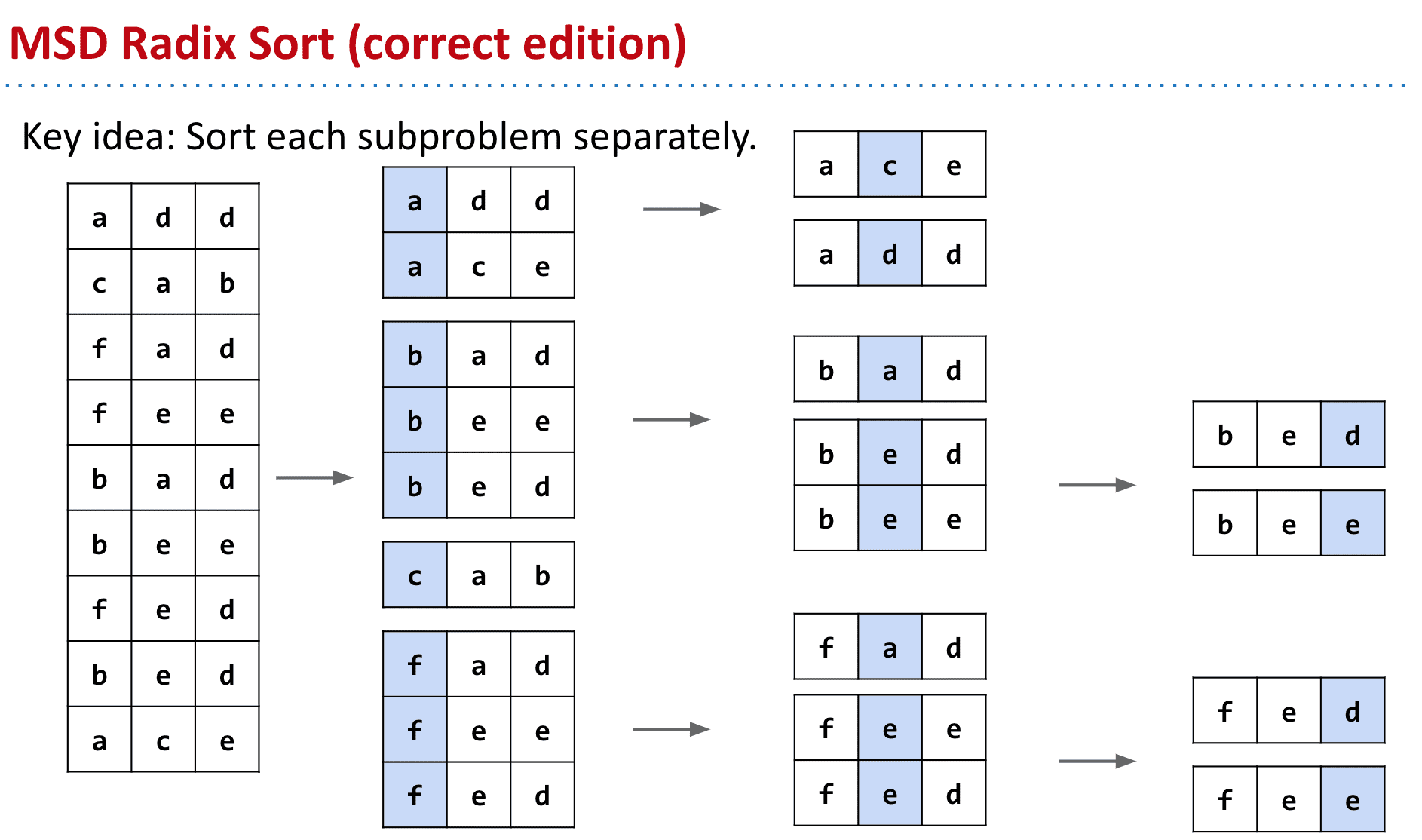
比较Radix Sort和选择排序的速度
这取决于排序的对象,如果他们非常相似那么LSD Radix会更快,如果相似度很低那么merge会更快
因为LSD从后面开始比对,而Merge比较依靠前面和不相似的字符来加快速度
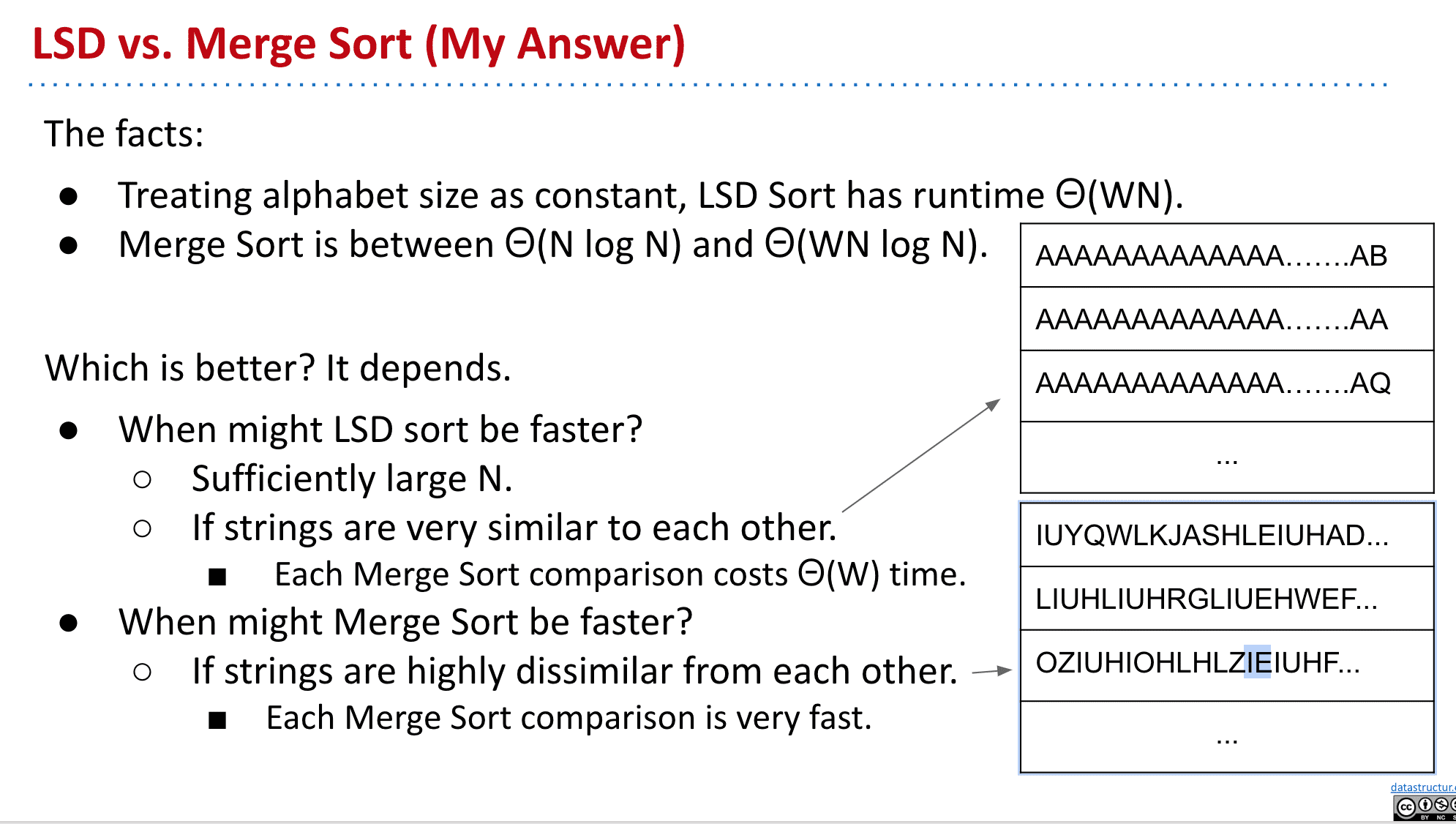
- Treating alphabet size as constant, LSD Sort has runtime Θ(WN).
- Merge Sort has runtime between Θ(N log N) and Θ(WN log N).
不过实际测试中(长度为100的相等String)merge却快了不少
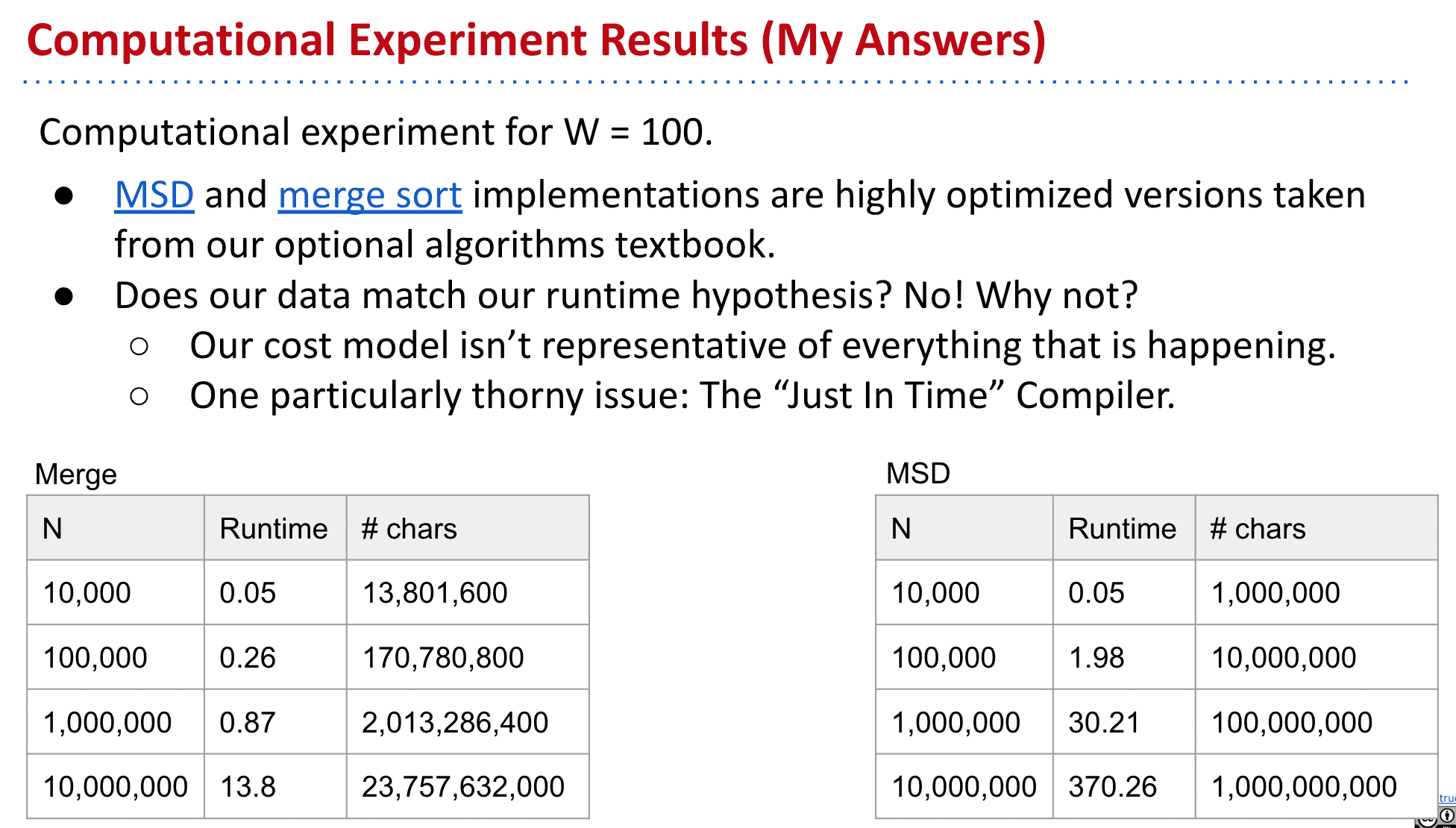
这是因为有JIT也就是即时编译在进行优化(just-in-time compilation)

让重复,不必要的操作都快了不少
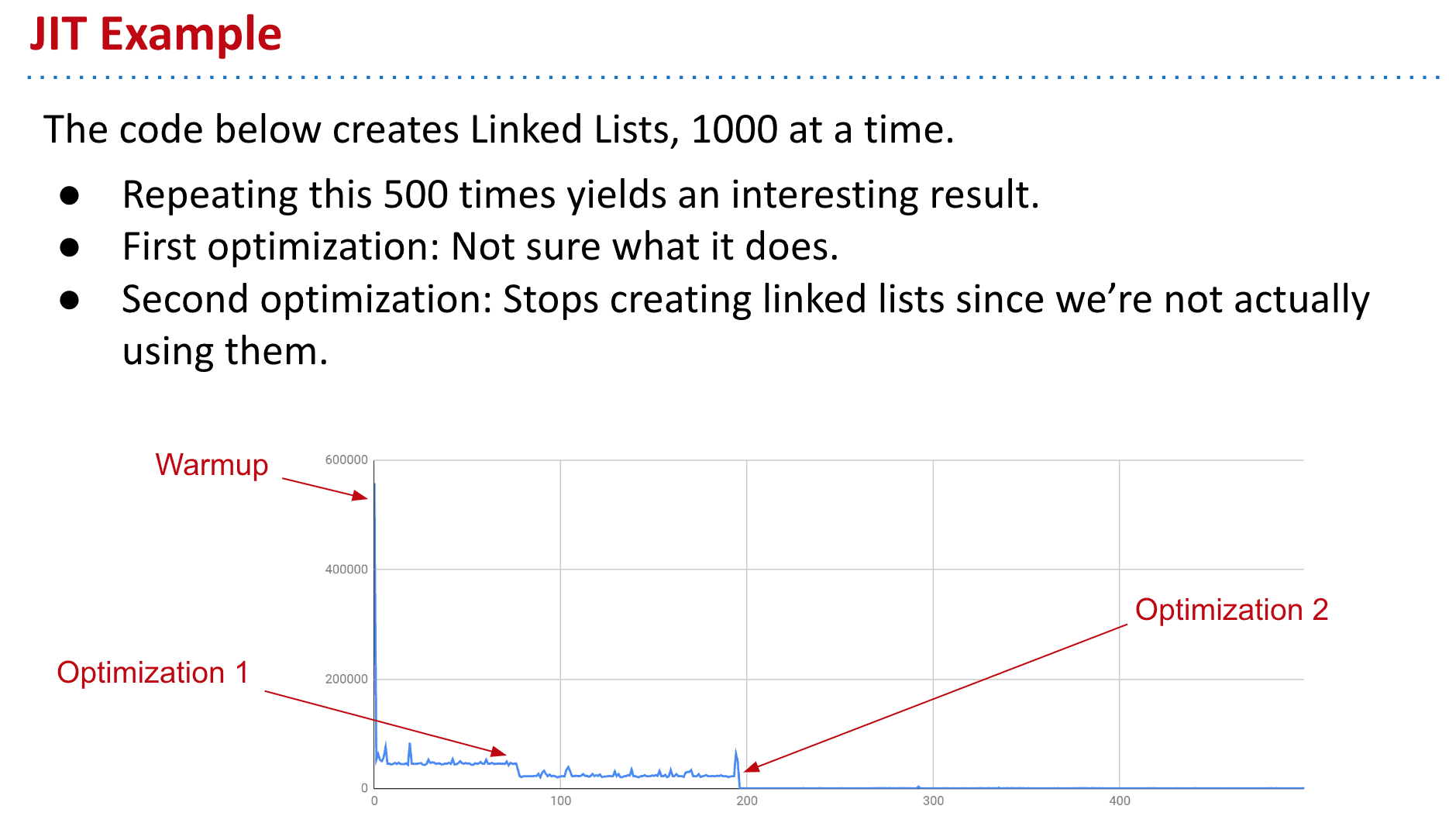
merge中不断生成新linklist的时间大幅缩短
当关闭JIT后就可以发现MSD确实比Merge快
但也不是理论值那样的字符调用,因为还有各种创建数组,移动,判断等消耗
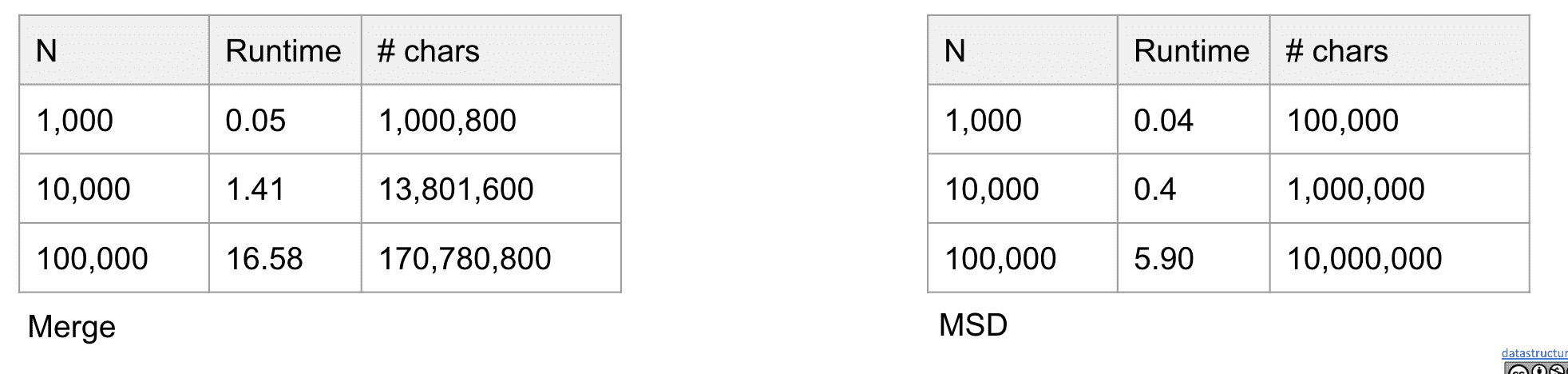
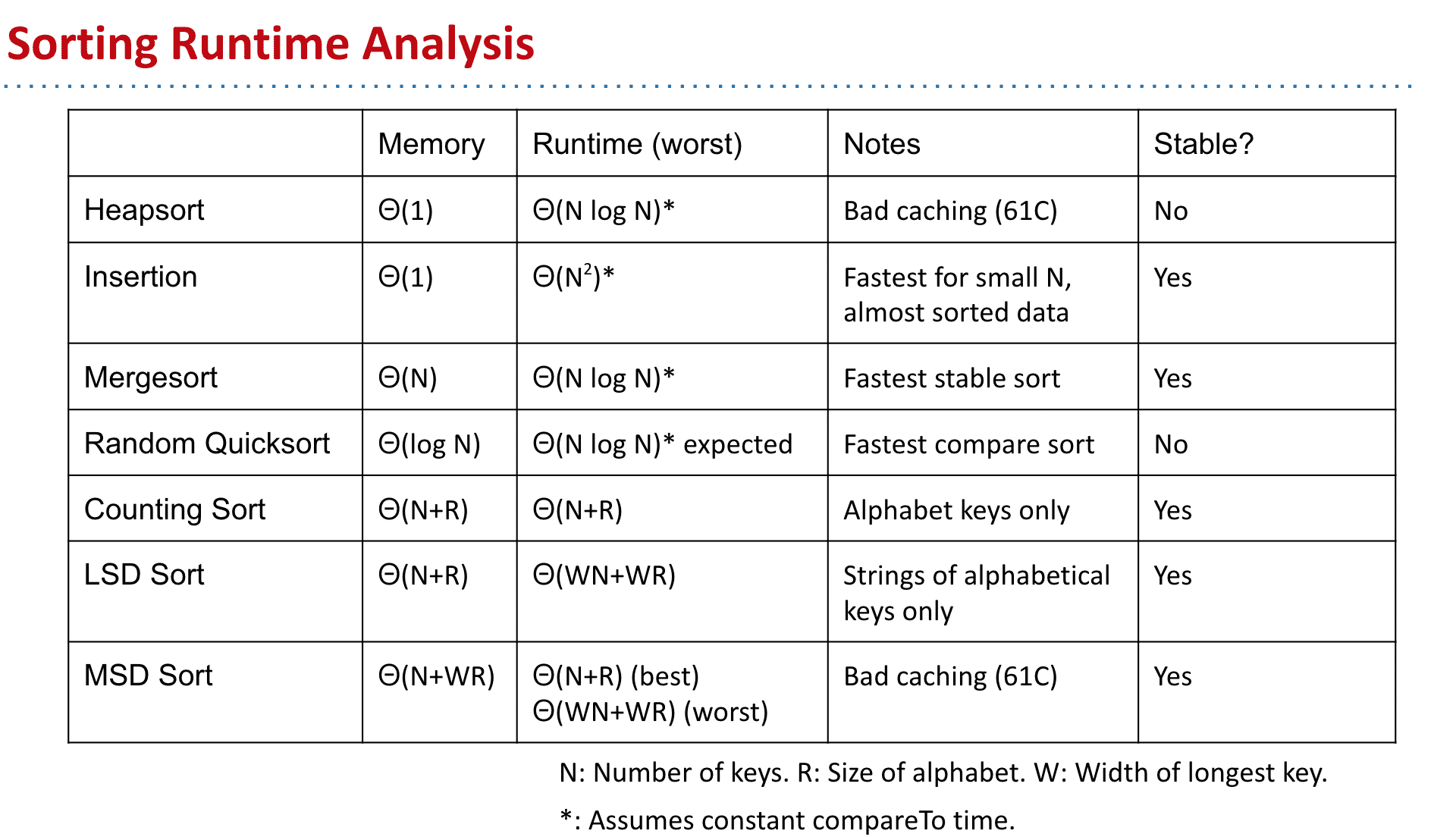
排序总结
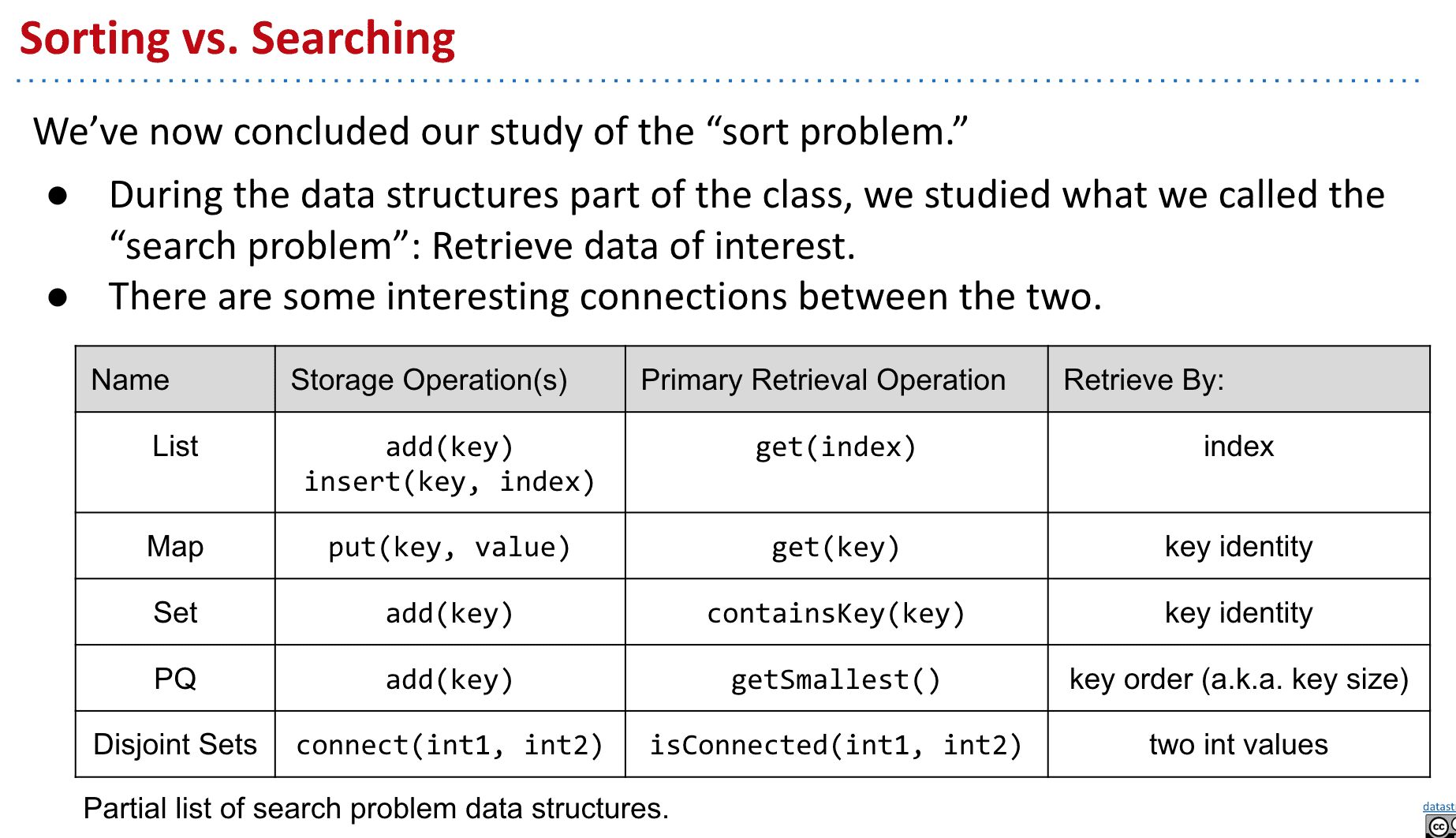
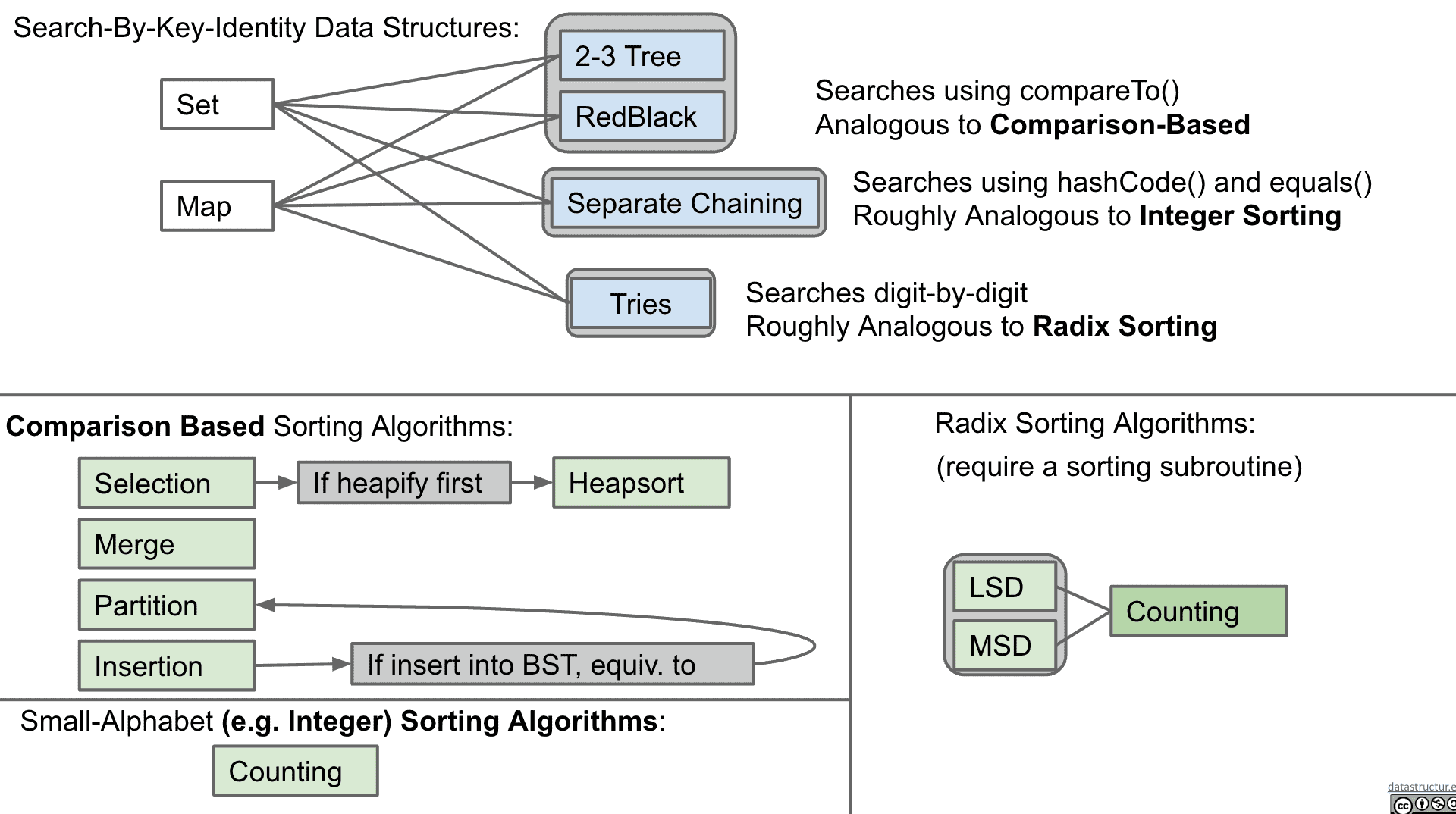
压缩 Compression
压缩可以让一段信息减少体积,经过解压后的文件与原文件没有不同
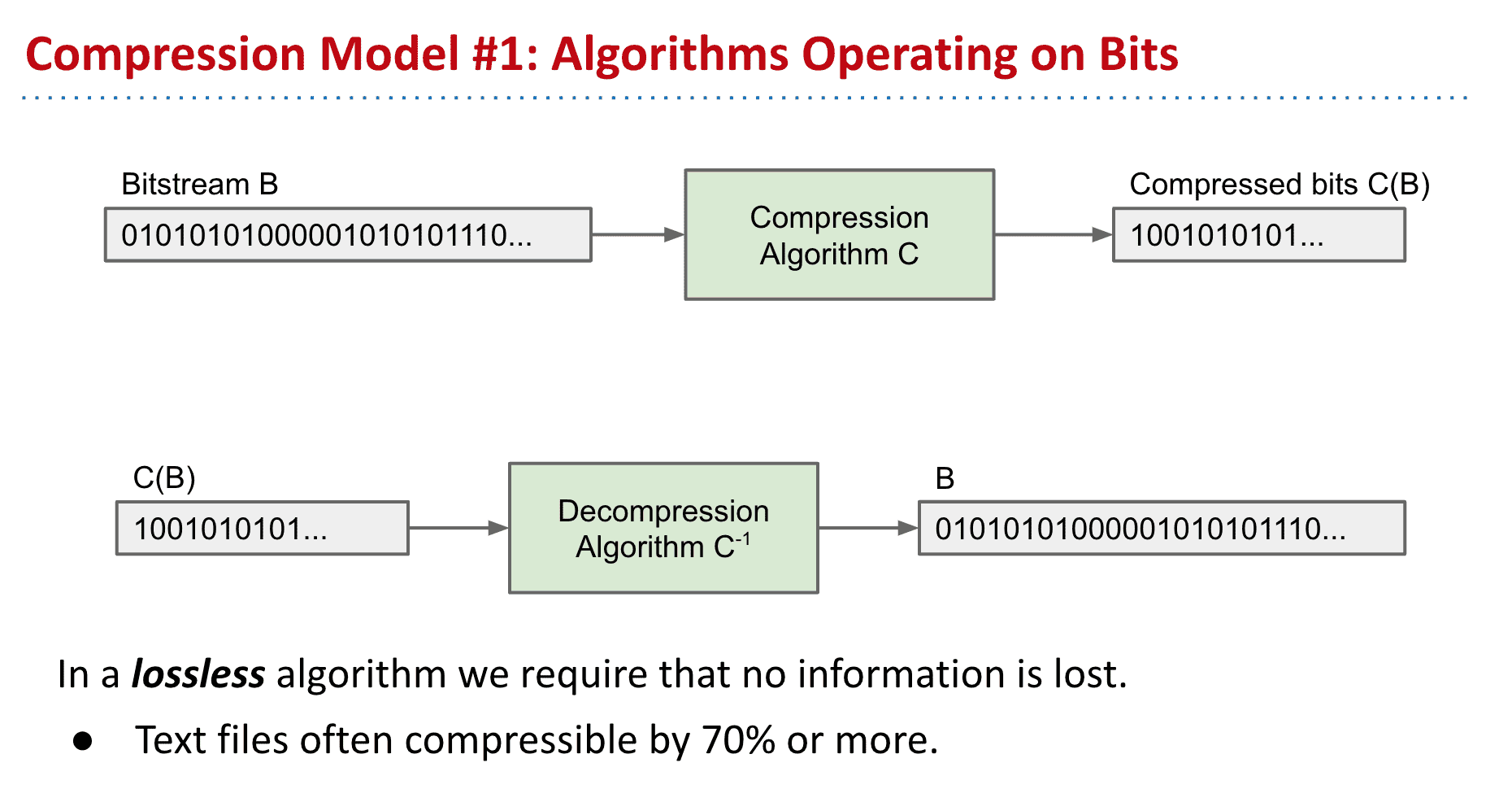
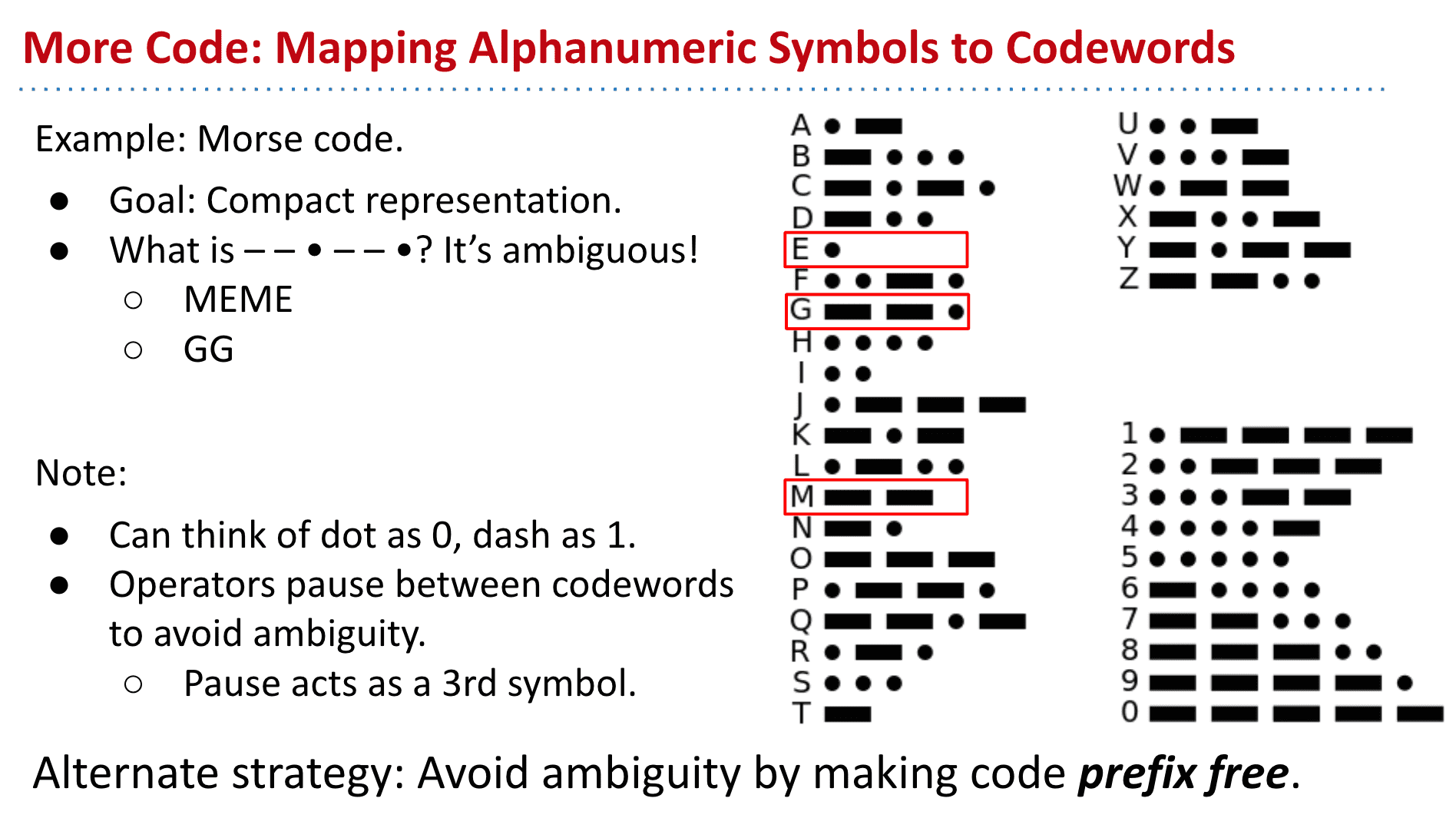
Prefix Free Codes
普通的无前缀编码
原本表现字母的方式比较占用空间

我们可以使用其他的方式来替代原本字符的表达方式来压缩
但是假如使用摩尔斯电码来代表的话,由于没有我们现实中使用时的那种停顿,同样的code可能代表不同的字符们
所以需要有一种方法来避免这种情况
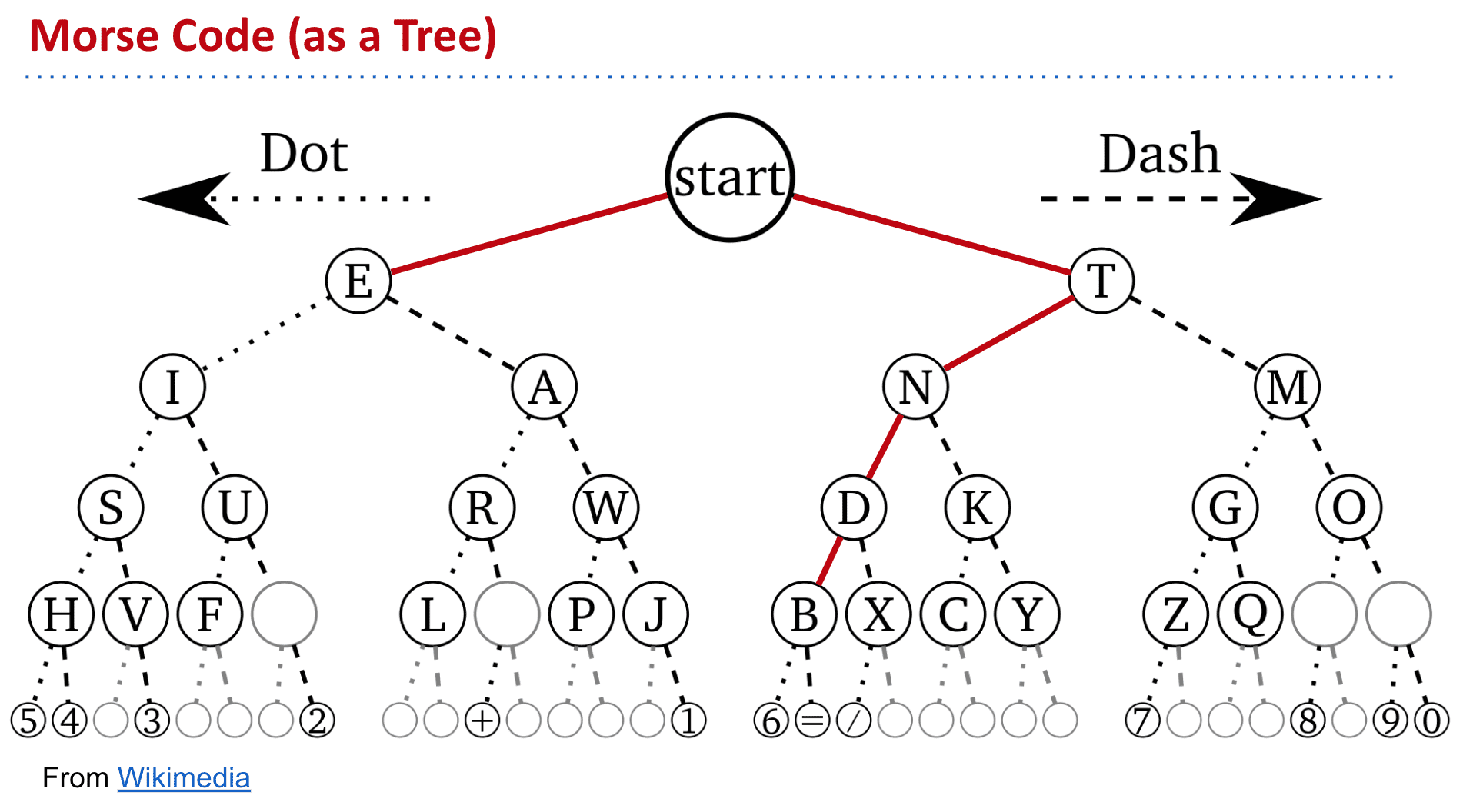
摩尔斯电码的tree
向左边是点右边是横
也就是说z的摩尔斯电码是:- - . .
于是我们可以设想一个Prefix Free 的tree
也就是没有一个字符码是另一个字符码的前缀
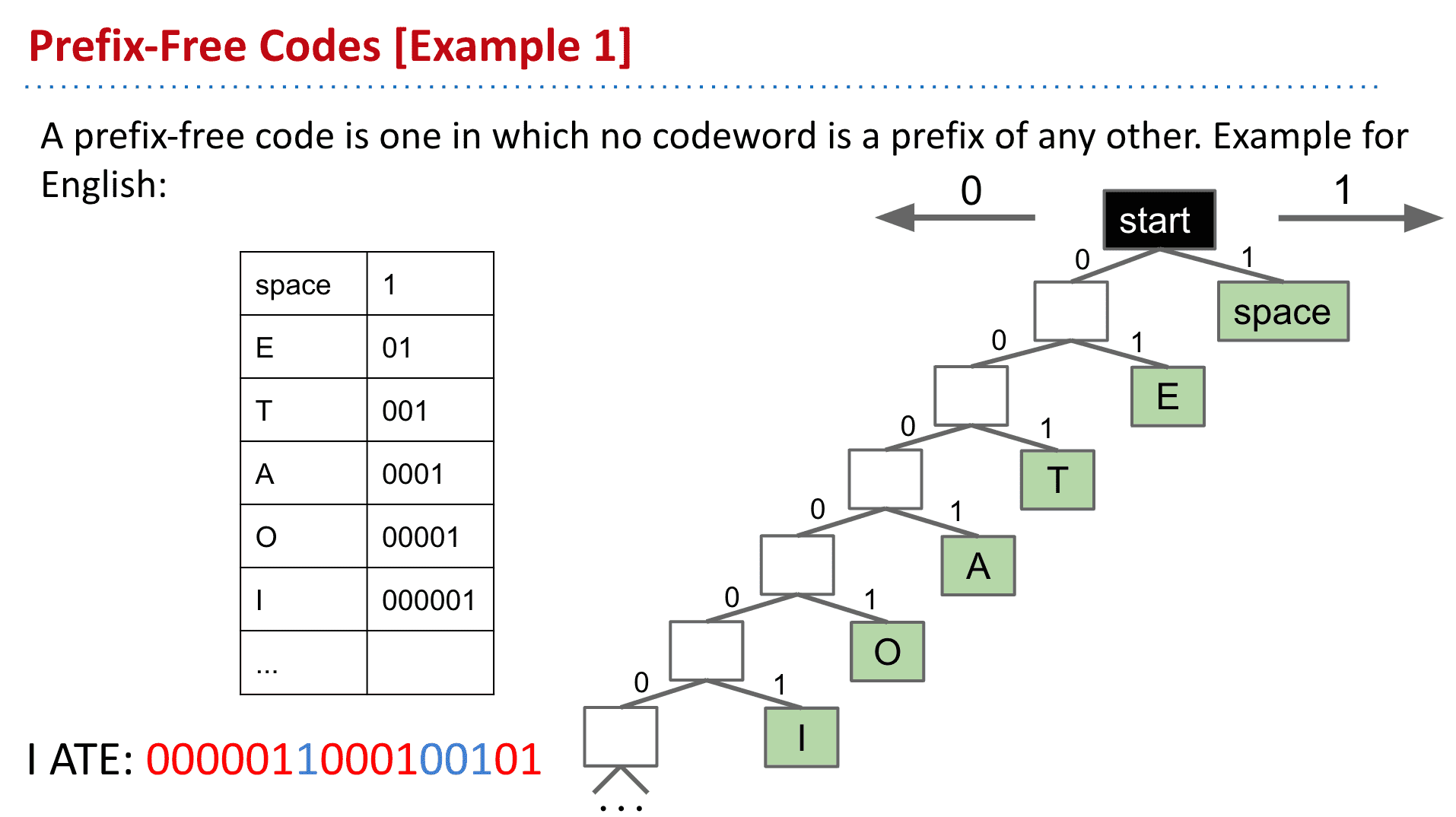
I ATE为例就能看到是以数0的个数来区分字母的
另一种更平衡的树
可以发现有代表的字符全是leaf,也就是最后的节点,同样避免了前缀问题
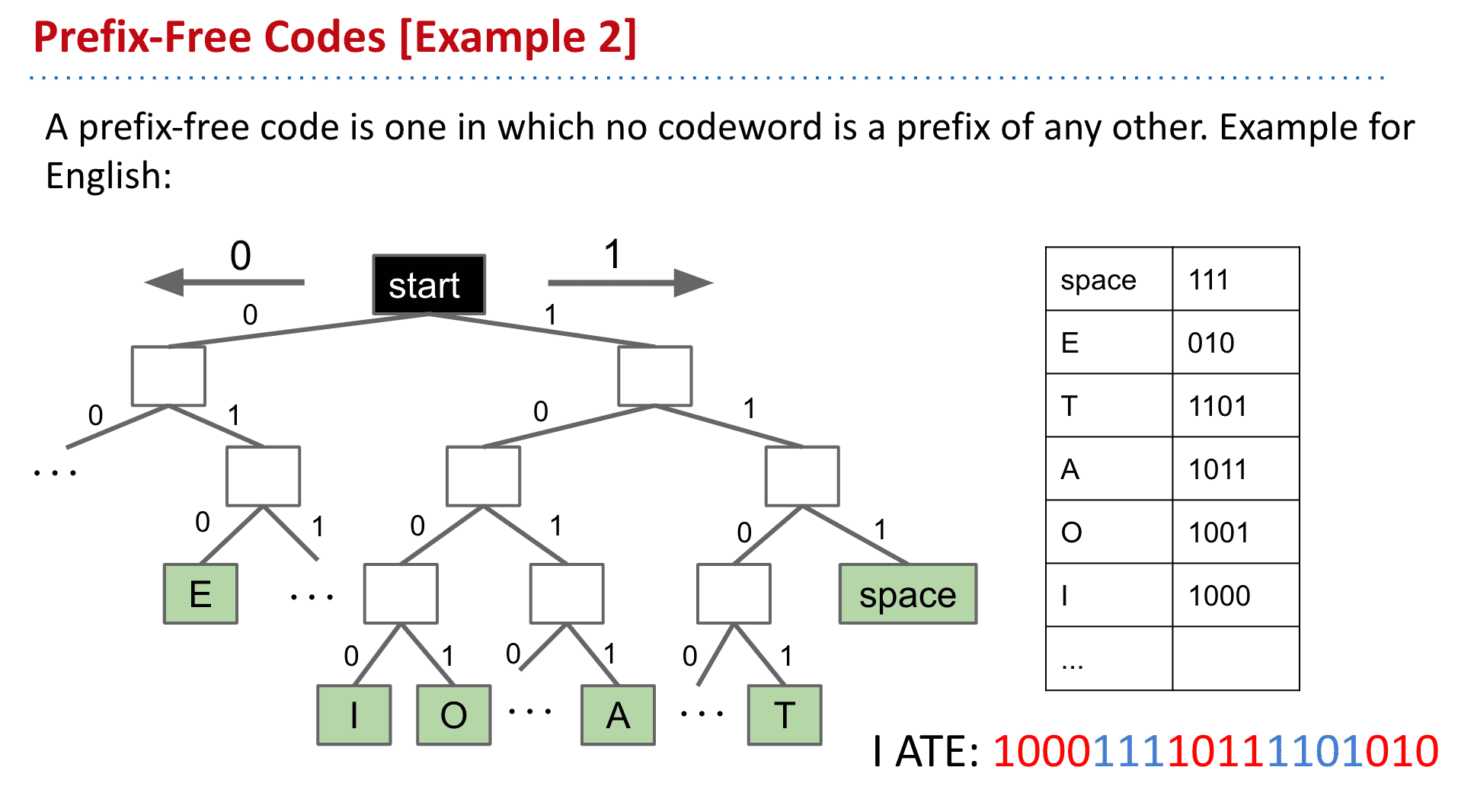
这第二种无前缀的tree相较于第一种,更加稳定
可以看到第一种越是后面的字符越长
而第二种却比较平衡
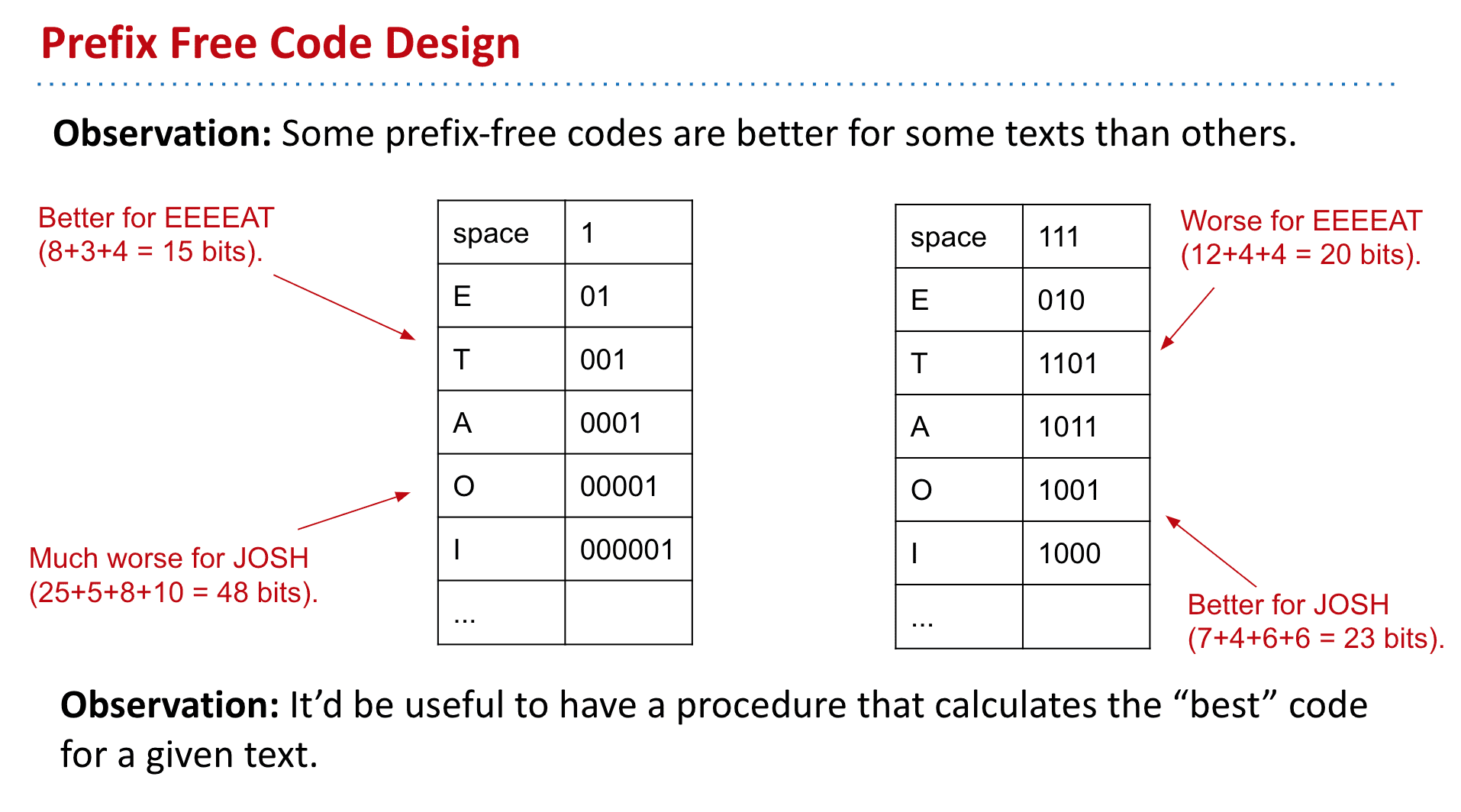
香农-范诺编码 Shannon Fano Codes
香农-范诺编码(Shannon–Fano coding)是一种基于一组符号集及其出现的或然率(估量或测量所得),从而构建前缀码的技术。
也就是按照字符出现的频次来建立一个tree,比如“我”和“爸”的频率加起来有一半,就放在左边

图里的“我爸是李刚”只是个非常小的字符集
这样一直按照频率分下去就得到了完整的tree
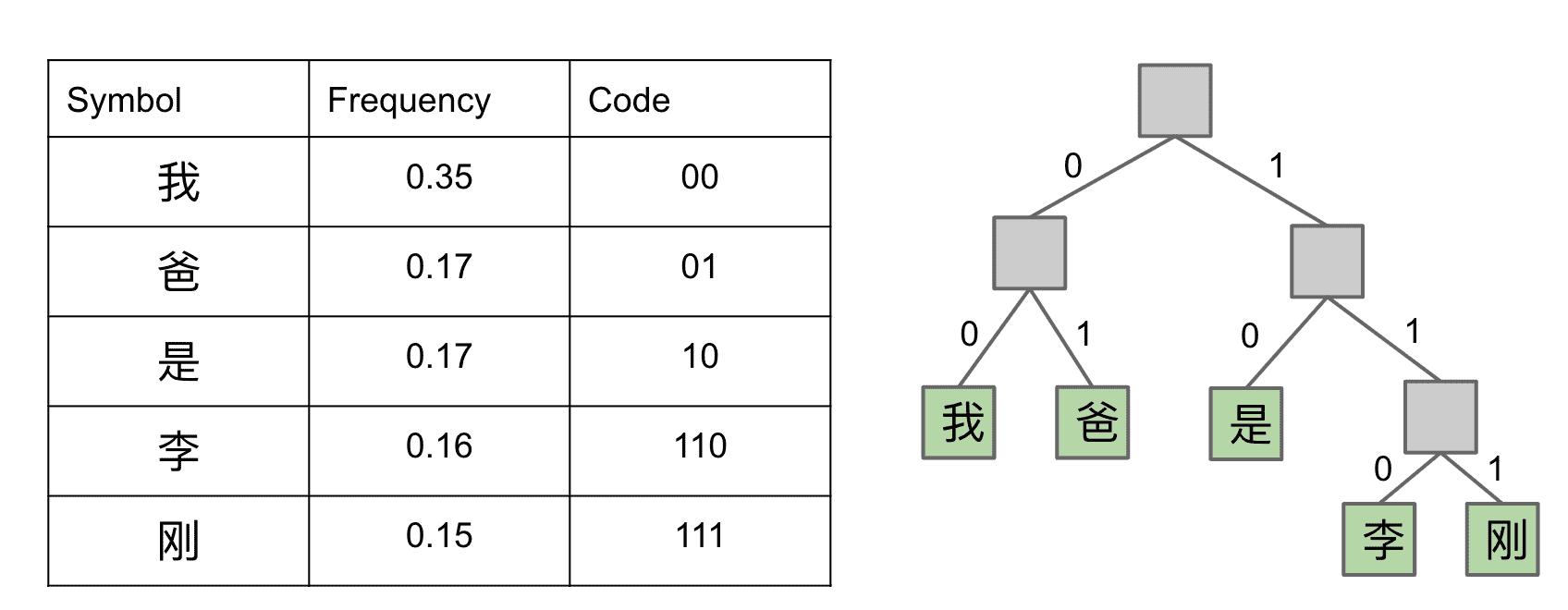
哈夫曼编码 Huffman Coding
与香农的相似,只是从由自上而下变成了自下而上

比如李和刚是出现频率最低的两个,就给他创建一个父节点(频率为他们相加)
这样不断的向上就得到了最终的tree
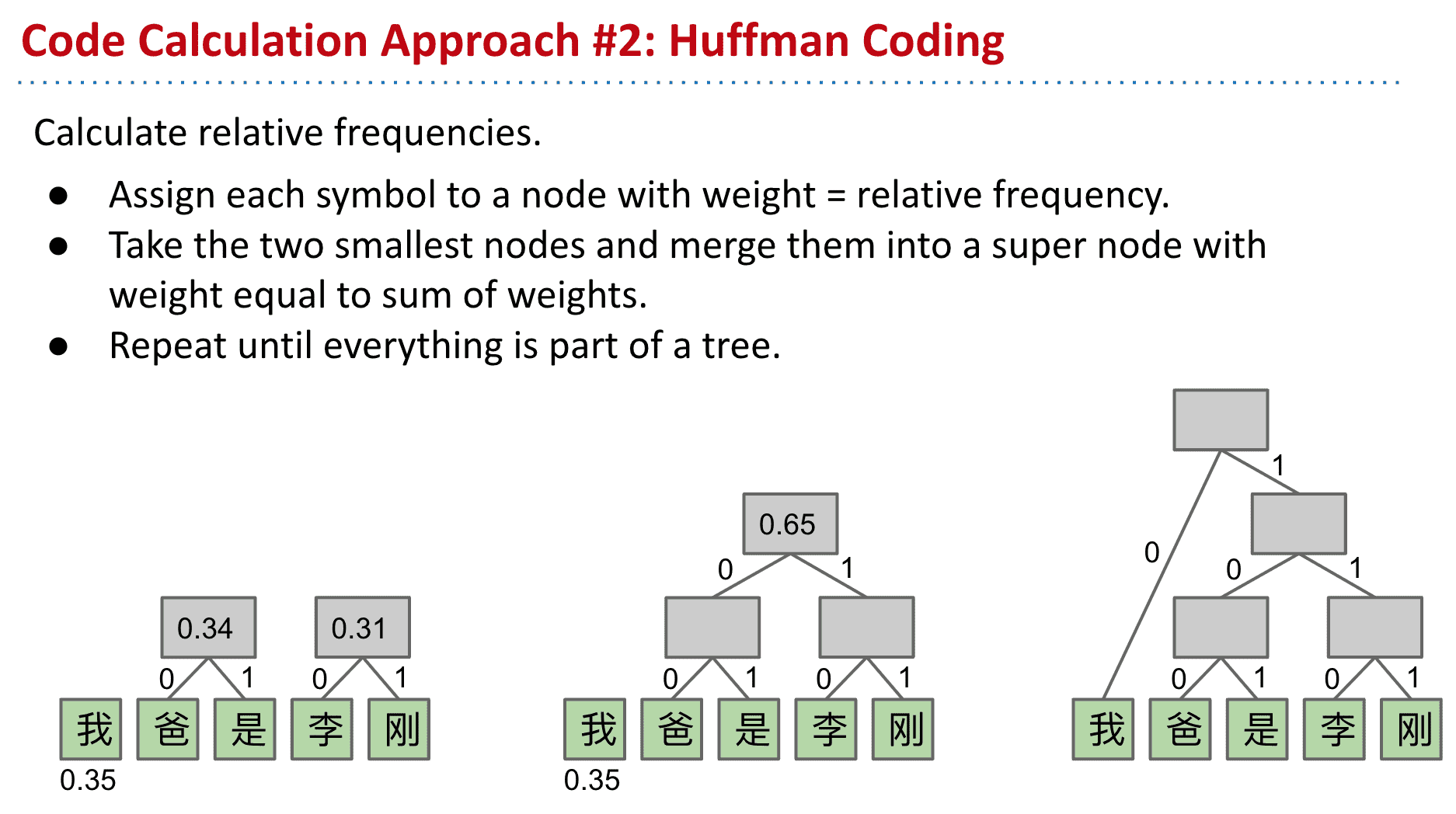
计算后得出平均每个字符只需要2.3个bits

中文字符一般使用32位的unicode来表示
如果一共有1000个汉字组成的文章话(在这里,字符集只有我爸是李刚五个字)
结果就如图所示,使用huffman的编码可以减少十几倍占用!

使用什么数据结构存储哈夫曼编码
压缩时
由字符→code:


有两种选择,一直很自然地就想到各种map,给他键值存入map
但也许数组也不错,我们可以使用字符作为index并存入对应的code
(注意字符其实也是整数,比如ASCII中“A” = 65,“a”
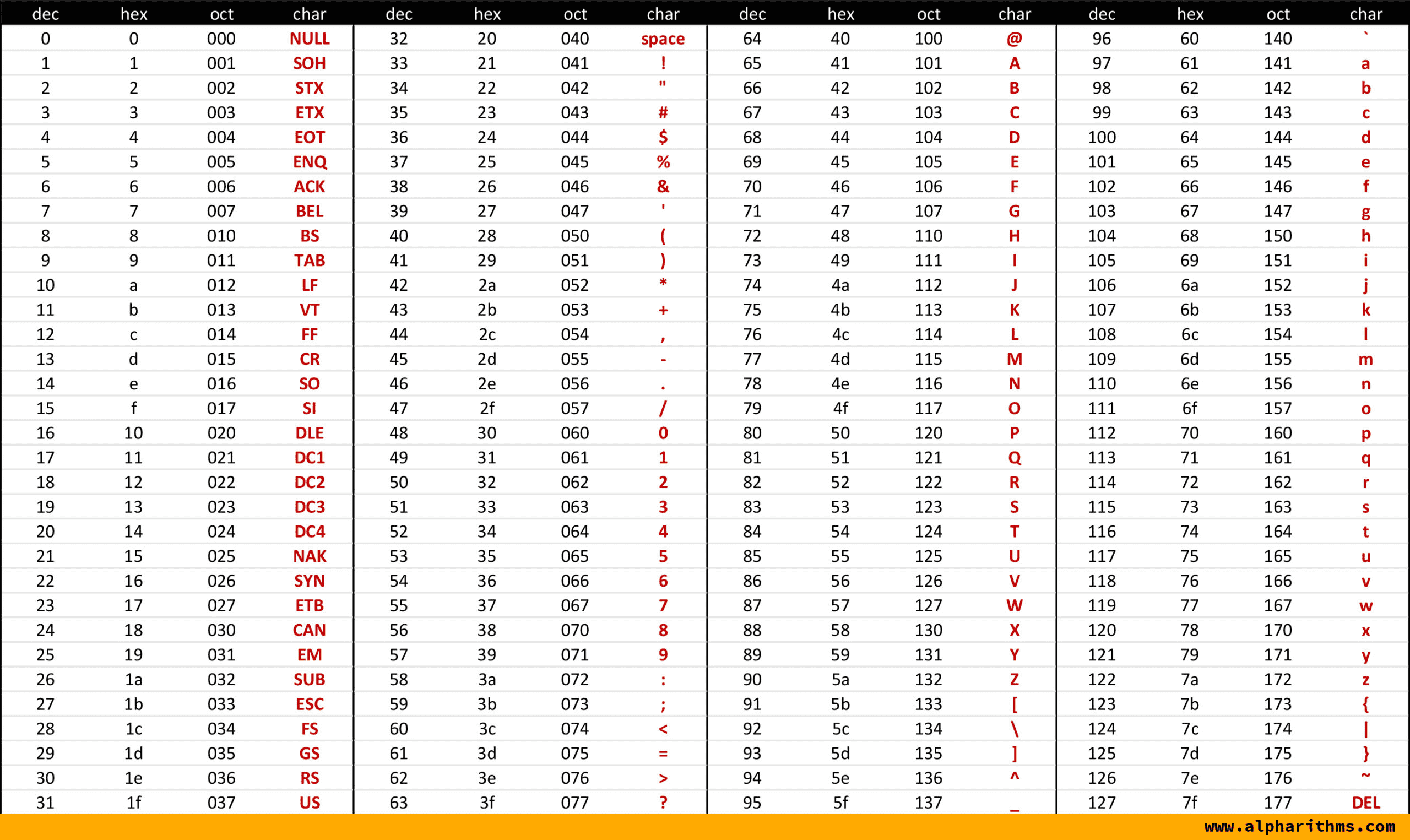
ASCII编码表
数组实际上就是一种由整数→其他对象的Map,他的效率更高一点.不过如果字符集太大的话也会浪费很多空间就是了
解码时
也就是code→字符
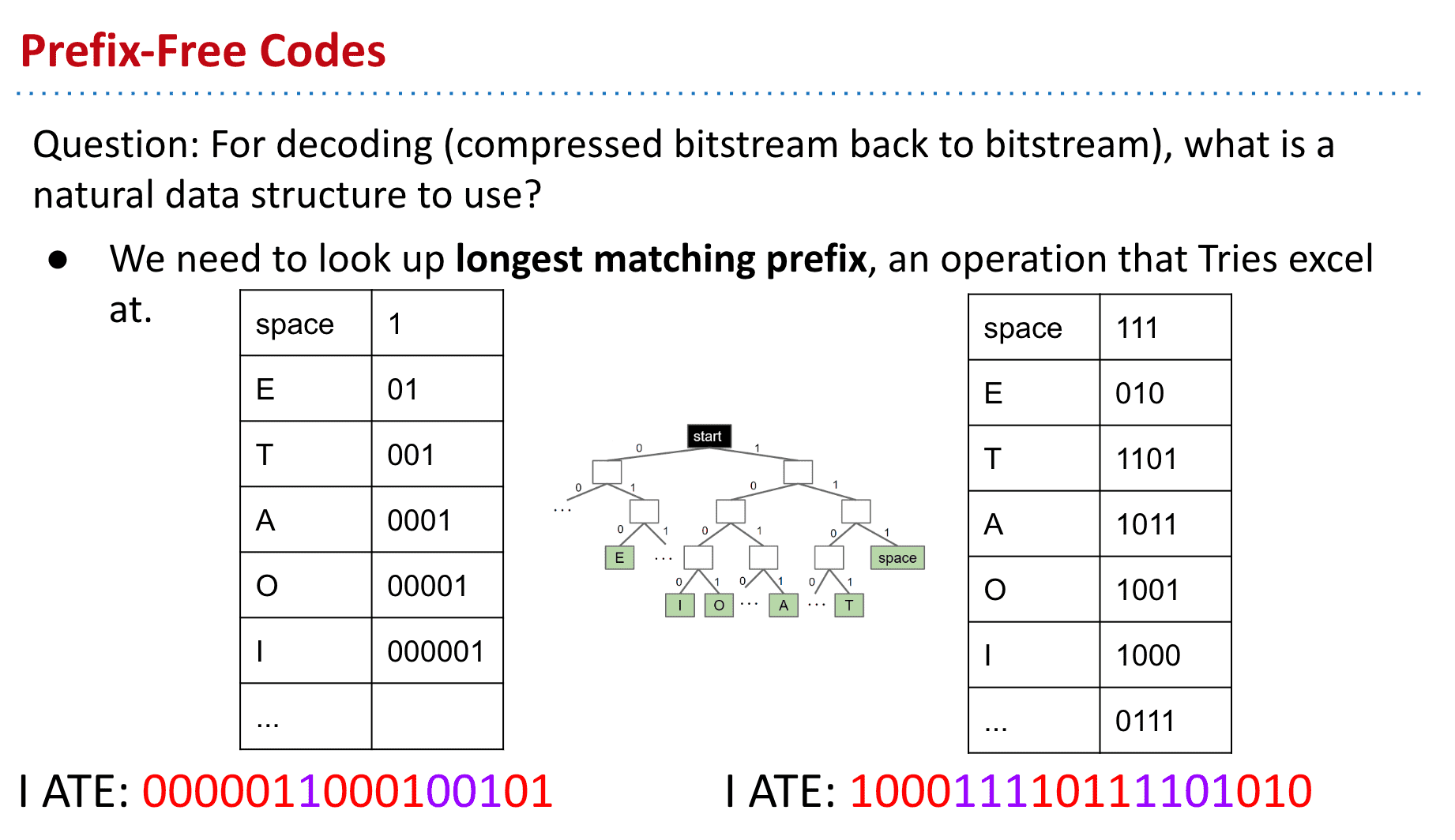
Trie也就是所谓的前缀树,字典树就很合适,使用binary trie**就可以很好的保存这些信息了
(这样似乎也让我理解了判断字符的问题,只要把编码一个一个到trie里找到字符后就开始找下一个字就行了,trie里存储的字符就相当于那些蓝色节点帮助断句)
我们拿到比如“1101”的编码后向左→左→右→左就找到了字符“T”
(从前面的编码也能看出来使用了某一种树来记录)
压缩时的编码方式选择
我们可以有两种方式来选择编码以压缩
1.对于不同的信息使用不同的编码集,比如英语文本使用英语的压缩)
这样做的好处就是不需要额外存储编码,但肯定也会影响压缩效率 毕竟不可能一篇英语文章就用掉了所有ASCII字符(也就是次优的编码)
2.我们可以被压缩的文件创建一个编码(语料库),然后和压缩后的内容存在一起.
好处是适用范围广,但会额外占用一部分存储

现实中采用了第二种方法
因为对于大量的文件一般语料库占用不了多少位置,但适用范围却光得多,不需要专门建立英语,中文等语料库
哈夫曼编码压缩与解压缩例子
压缩:计算字符出现频率→建立一个压缩数组和解压字典树→将字典树加入压缩文件→讲压缩后的信息也放入压缩文件
Codewords的部分就是由我(https://nhuji.github.io/post-images/%25E6%2588%25AA%25E5%25B1%258F2022-10-17_14.54.27.png)
Demo
Codewords的部分就是由我(0)我(0)刚(111)刚(111)……等组成的,因为没有相同的前缀,所以解压时也不用担心断句问题,比如11在trie上没内容,1111更没有内容 到111就只能停下并找到对应的“刚”了
解压:
先读取语料库(trie)→然后在codewords里寻找最长前缀并输出字符
这样一个过程完成后就成功解压了

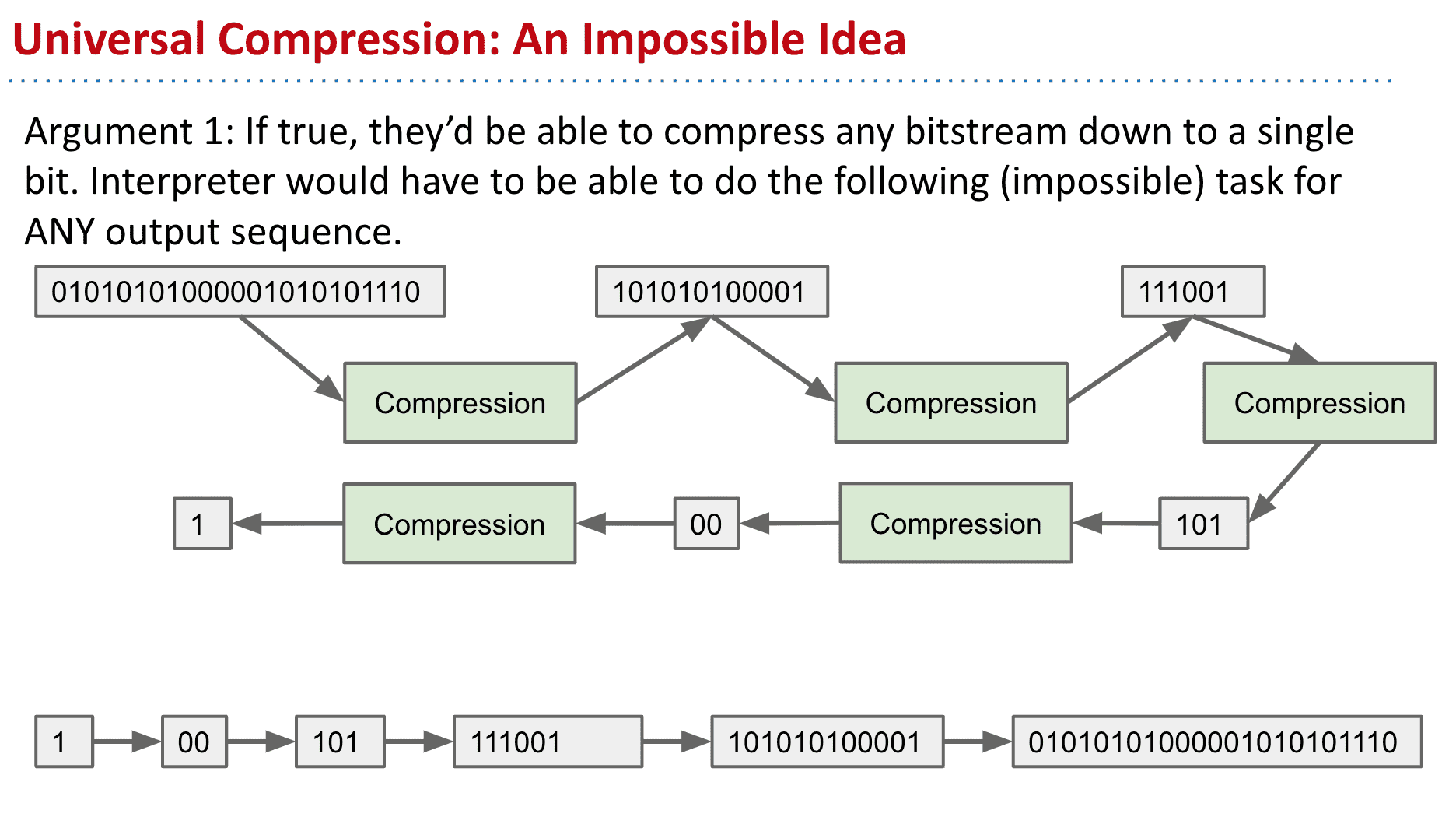
有没有可能有一种能压缩50%以上体积的算法(通用的情况下)
当然不可能,因为可以做到的话就能一直压缩直到用1bit表达巨量的信息(一般情况下的压缩效率好像在70%左右)