主要介绍了数据结构相关的内容,包括命令行参数、渐进符号、并查集、抽象数据类型、二叉搜索树、B树、红黑树、散列表、优先队列、图、最短路径和字典树等。同时还涉及了软件工程中的复杂度定义和拓扑排序等内容
这个博客并不是我最初写这篇笔记地方,所以可能出现各种包括发布时间、文字、样式等错误
Week 5
命令行参数
public static void main(String[] args)
我们知道public公共的、static静态不被实例化、void返回为空、main就是main
那么(String[] args)是什么呢 其实就是接受的参数
比如
public class ArgsDemo {
/** Prints out the 0th command line argument. */
public static void main(String[] args) {
System.out.println(args[0]);
}
}
再在终端使用它
nhuji@huhudeMacbook Desktop % java hello big bug
big //得到的结果
就会把我们打进去的big bug的第一个big打印出来,如果替换成System.out.println(args[1]);就会打印bug
一个使用参数的例子,会返回相加的值
如何更有运行效率
之前的课程我们并不关心运行情况,而现在到了数据结构这一部分
我们就需要关注怎样能更高效的运行程序了
对于如何衡量程序是否有效率,我们可以从它循环多不多之类的的来看,
但很不精确,所以我们可以使用类似time之类的计时器来比较,不过根据机器性能、具体参数等差异会很大,另外也需要我们等待运行结束,像之前的[Lab3 时间测试 resume按钮 随机比较 创建执行断点 ] 使用的Stopwatch也是类似的东西
所以可以按照运算次数来进行比较,还有更准确的符号表示(算是概括了)


为什么说dup2比1好呢:
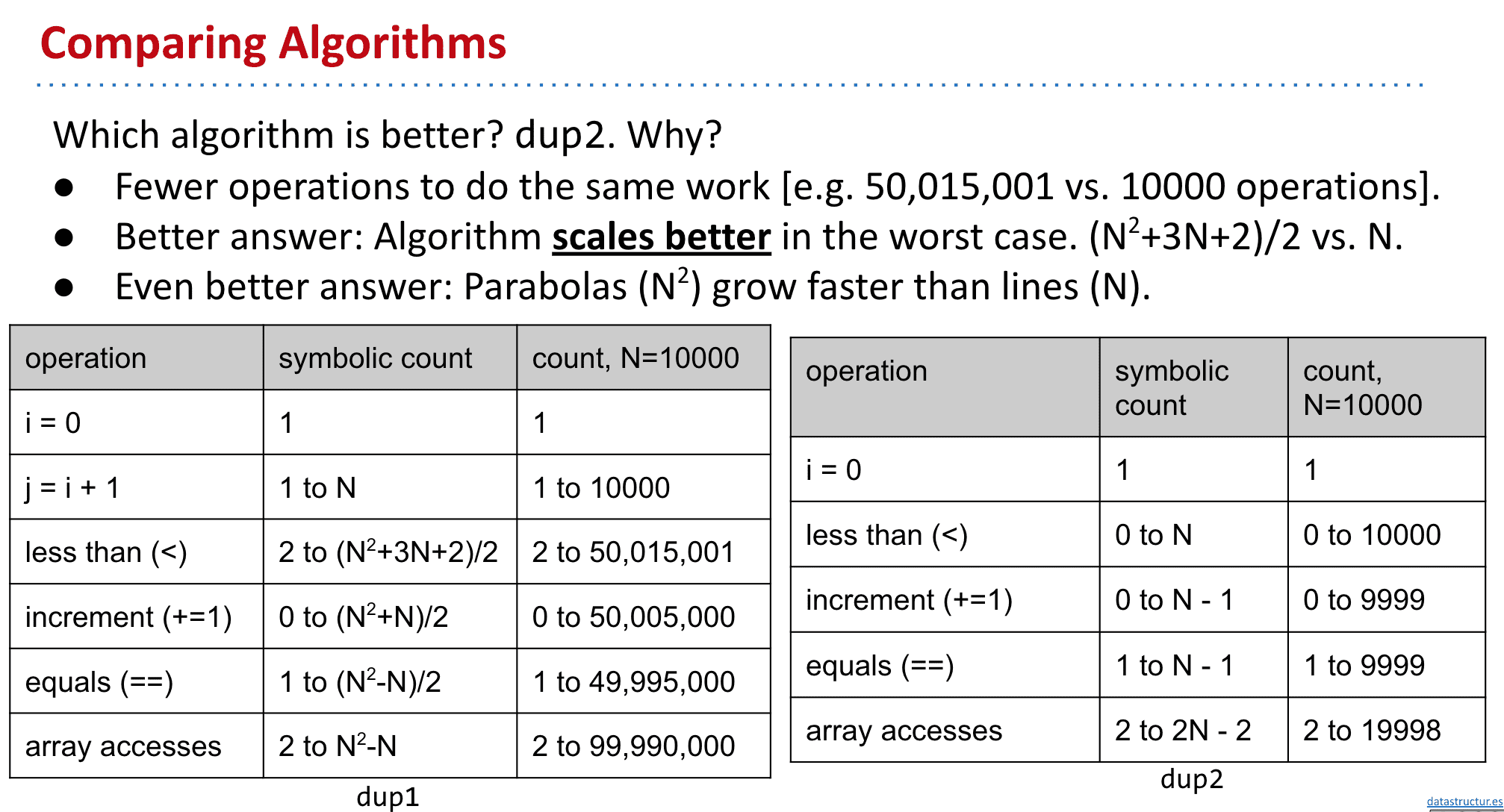
scale很重要,当N足够大时差别就很明显了
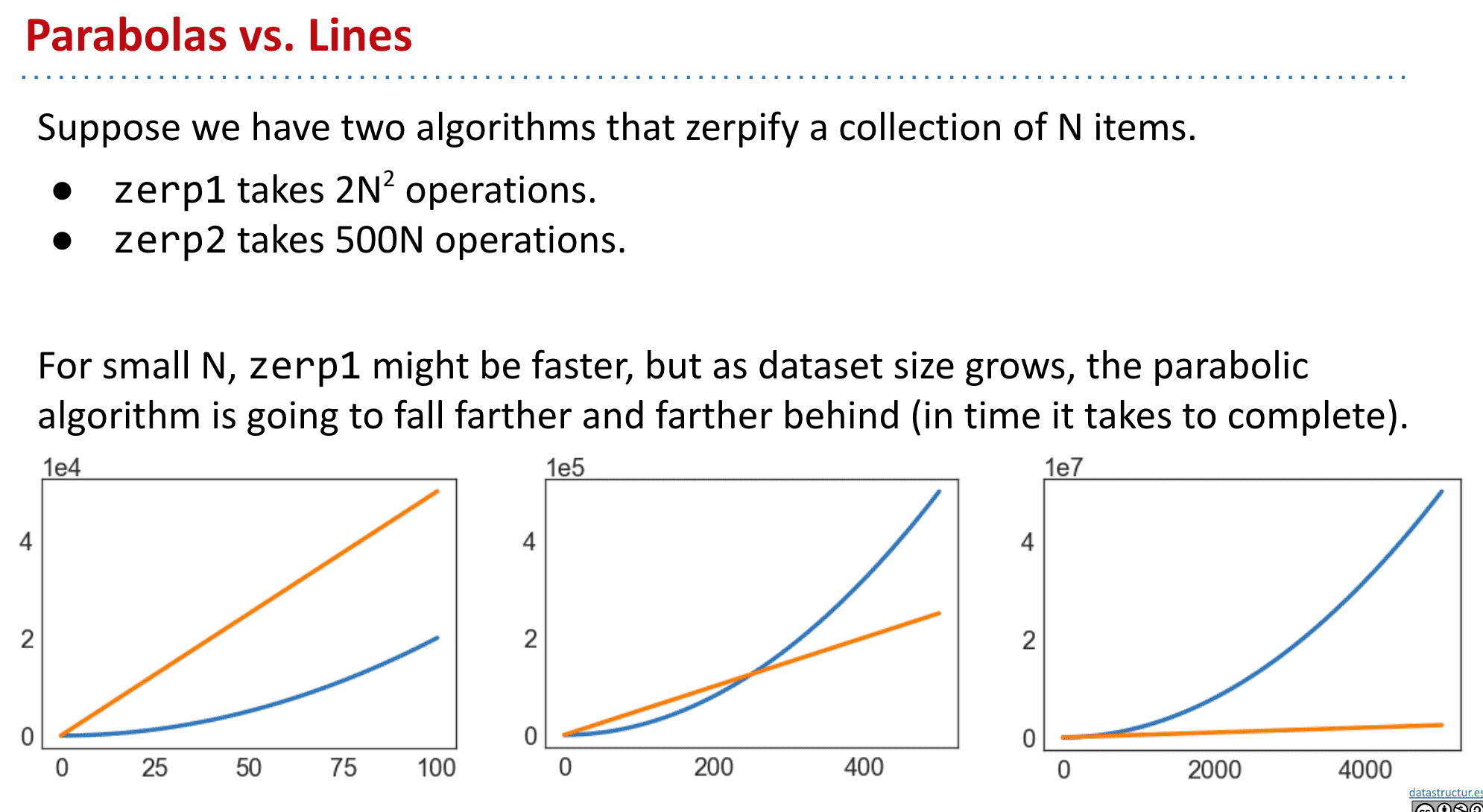
如同数学里算极限一样,当大到一定程度后其他常数(包括常数乘法)什么的都可以忽略掉,我们只关心order of growth(一个算法的增长顺序是随着输入大小的增加,运行一个计算机程序所需时间的近似值。增长顺序忽略了固定操作所需的恒定系数,而是关注与输入大小成比例增加的操作。)
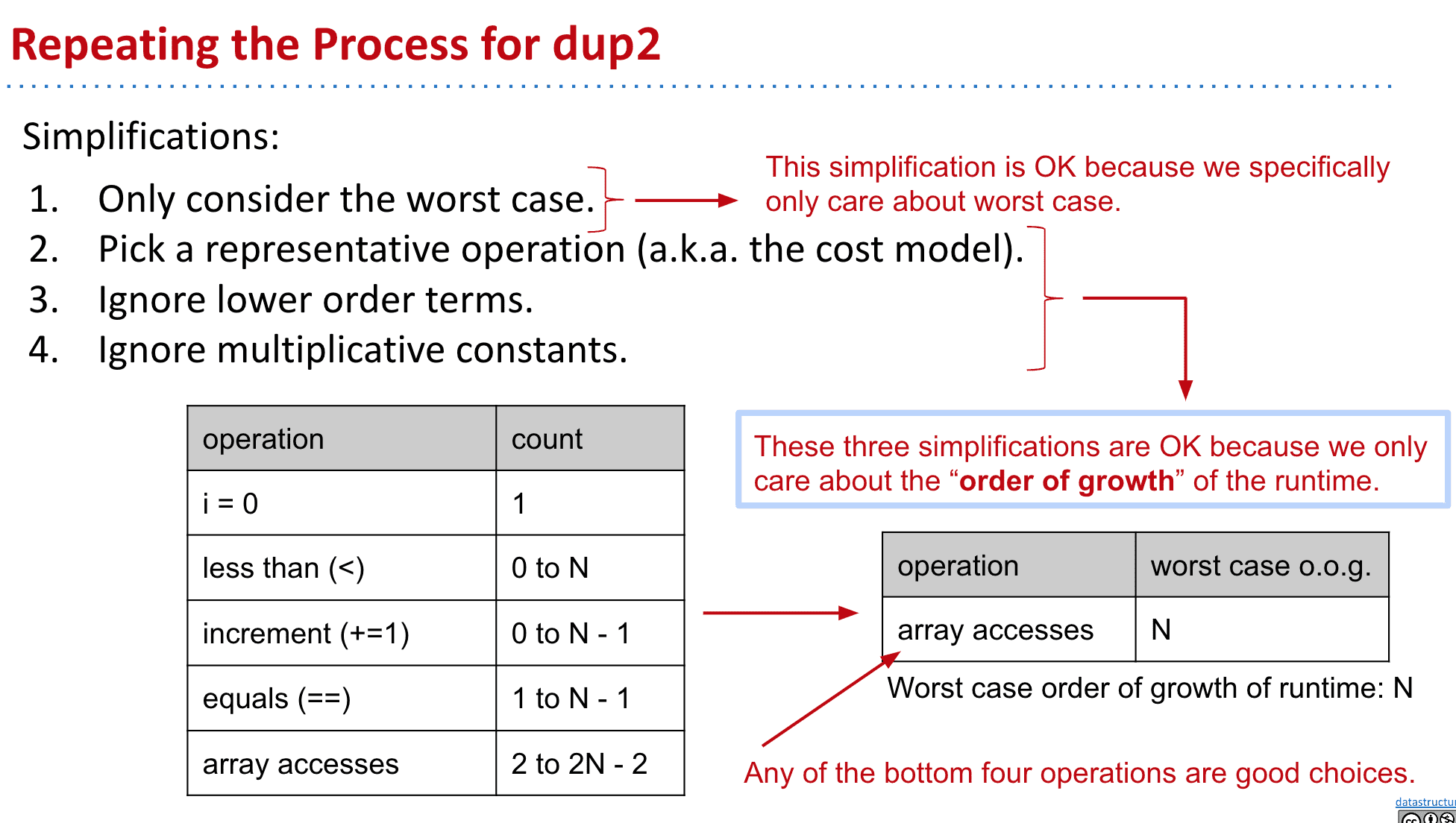
虽然简化后不错,但我们可以有更简单的衡量速度的方法
选择一个代表操作(cost model),后化简


渐进符号 asymptotic notations 渐进分析part1
Big-Theta 符号
被用于描述order of growth


使用的例子
比如表示 属于这个家族
Big O 符号
不考虑下界限了

这部分似乎微积分也有类似的,或许学到相应的东西后会更理解,也说明了数学在计算机中的重要性
Week 6
并查集 Disjoint Sets data structure
用于处理不交集(Disjoint Sets)是否连接,和进行连接
简单来说就是可以查两个东西有没有关联
Disjoint Sets就两个方法,用于连接元素和查看他们是否连接:
public interface DisjointSets {
/** Connects two items P and Q. */
void connect(int p, int q);
/** Checks to see if two items are connected. */
boolean isConnected(int p, int q);
}
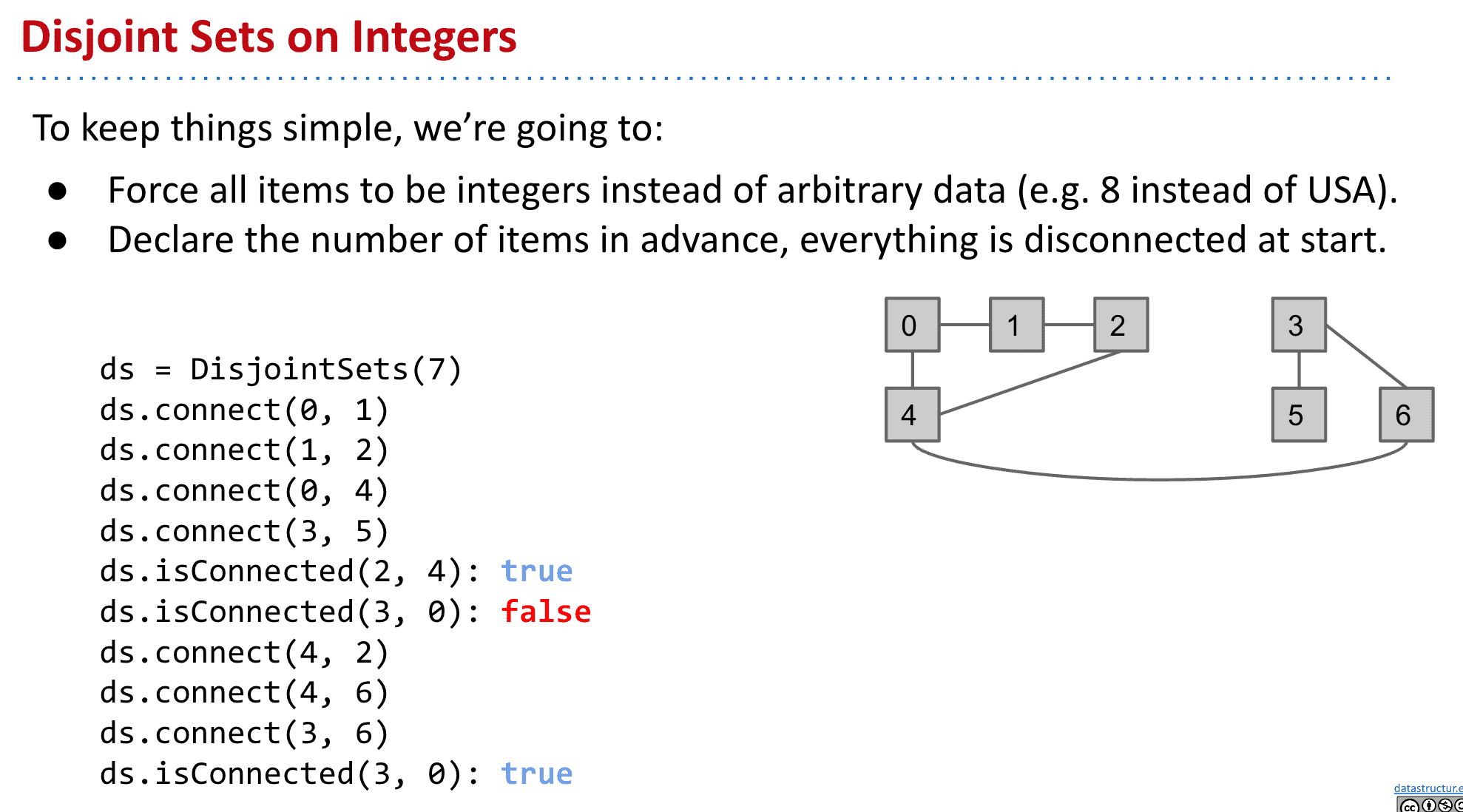
但是如上面的链接,记录每一个元素之间的连接,查询时可能会进行某种迭代、循环
在元素量巨大时很不高效
使用List<Set>组建
我们其实不关心他们怎么连接的,而只关心他们有没有连接

所以只需要记录每个元素属于哪个连接组件(Connected Components)
我们可以使用Java中的 List<Set
但是使用这种内置数据结构作为底层,速度会很慢很慢
比如我们要找5和6是不是连接的,就需要从头check一遍
使用int[]来组建
所以我们可以使用相对好一点的int的数组来建立这个结果
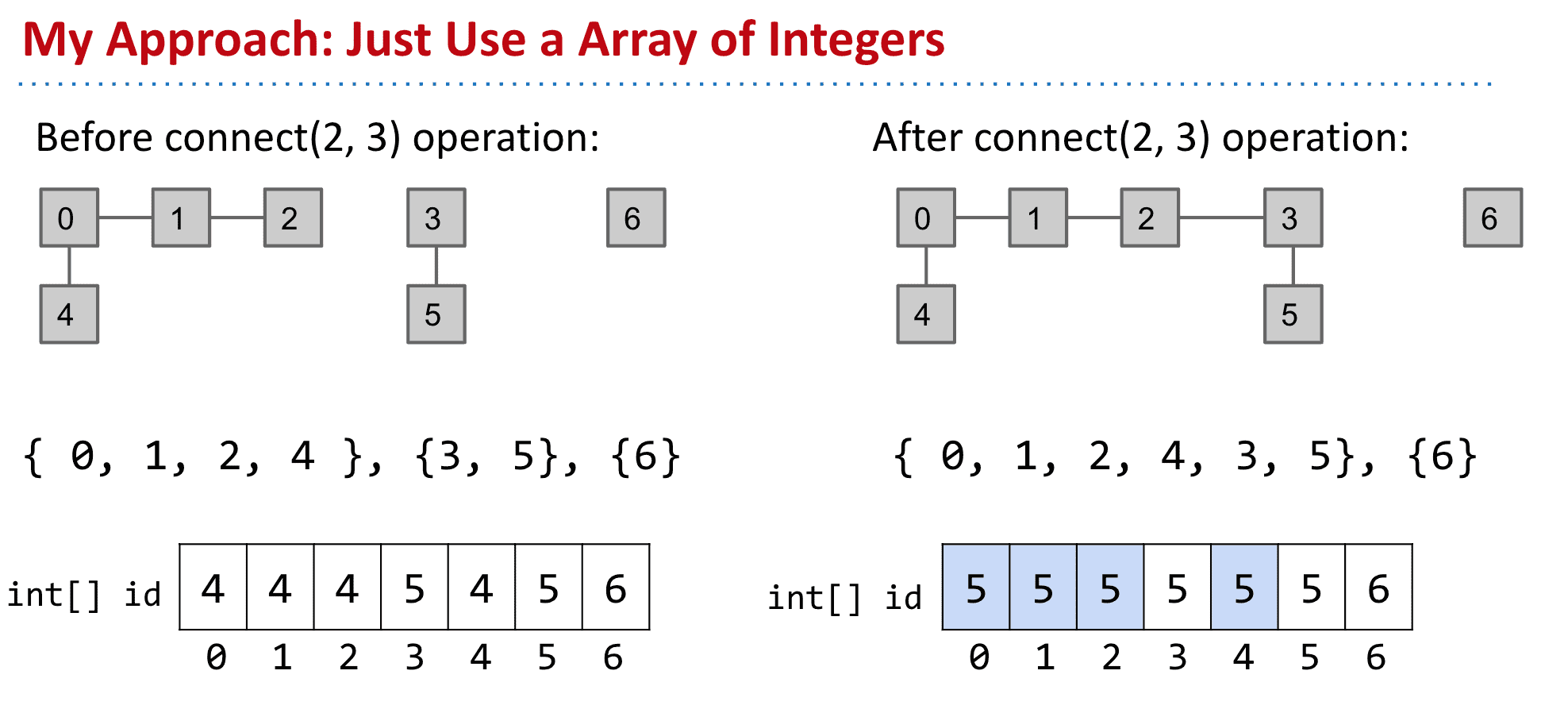
index是我们的数,而存储内容是他们的set
(只是个代表,只要是一样的数说明他们是一个连接组件就行)
而进行连接改变他们的存储内容就行了
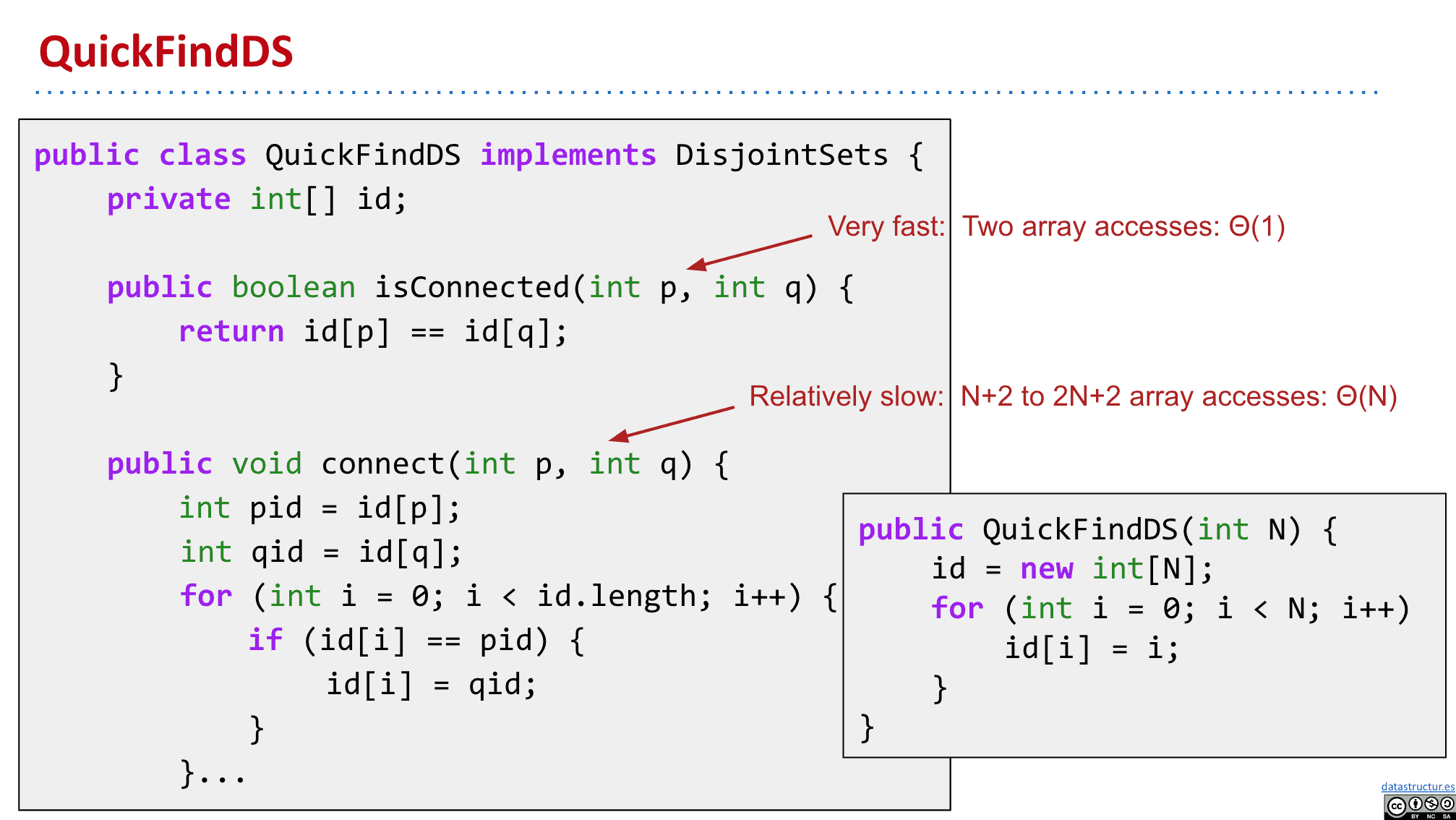
大概的实现
这么做的好处是执行isConnected会很快,只需要他们内容是否相等
(isConnected从O(N)→Θ(1))
使用Quick Union组建(改进)
和上面存储不同的连接组件ID不同的是,改为存储父级
-1表示根,而其他的存储元素的上一个节点
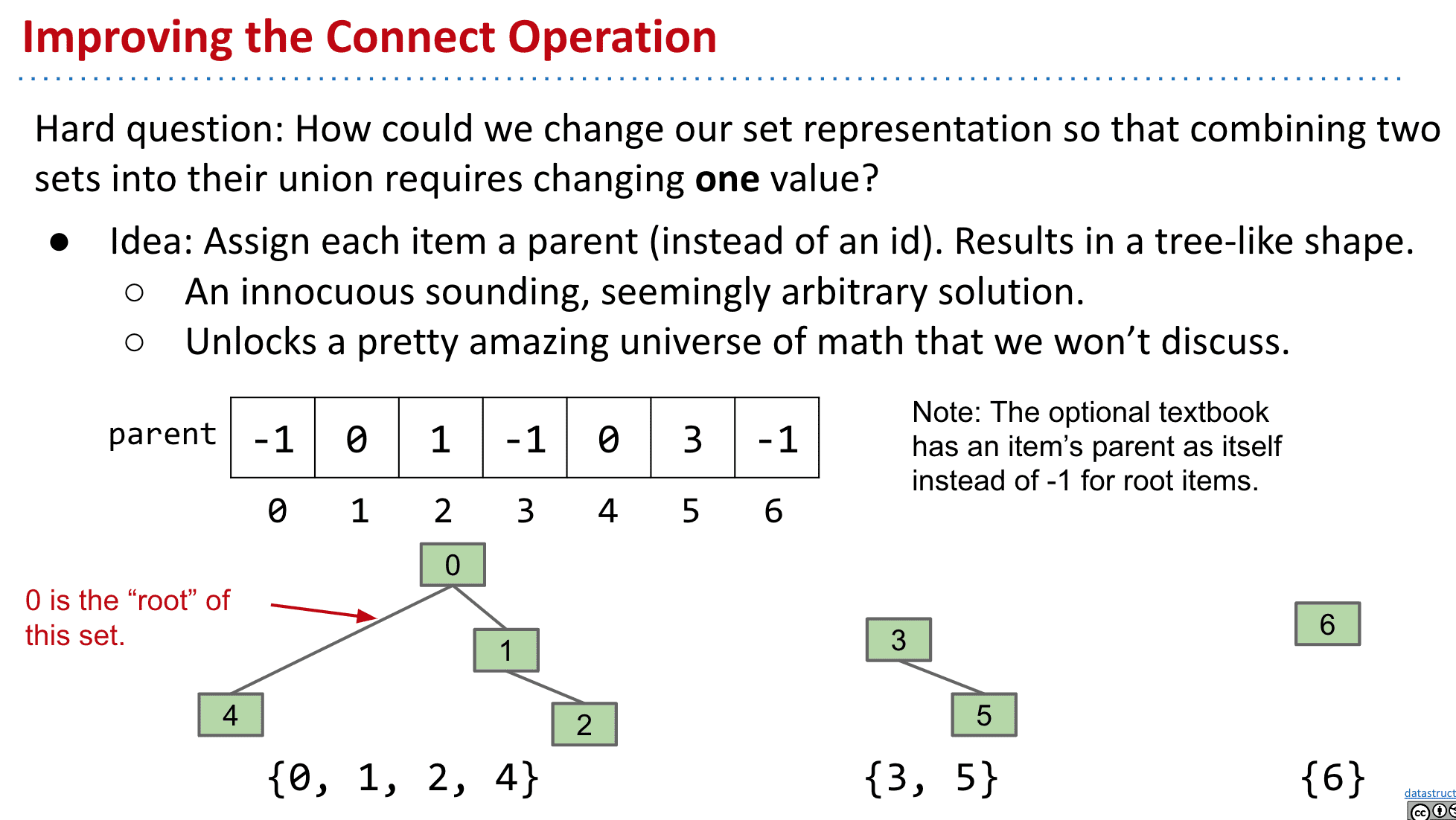
这样进行连接时,只需要把一个连接组件的根改为另一个根的元素
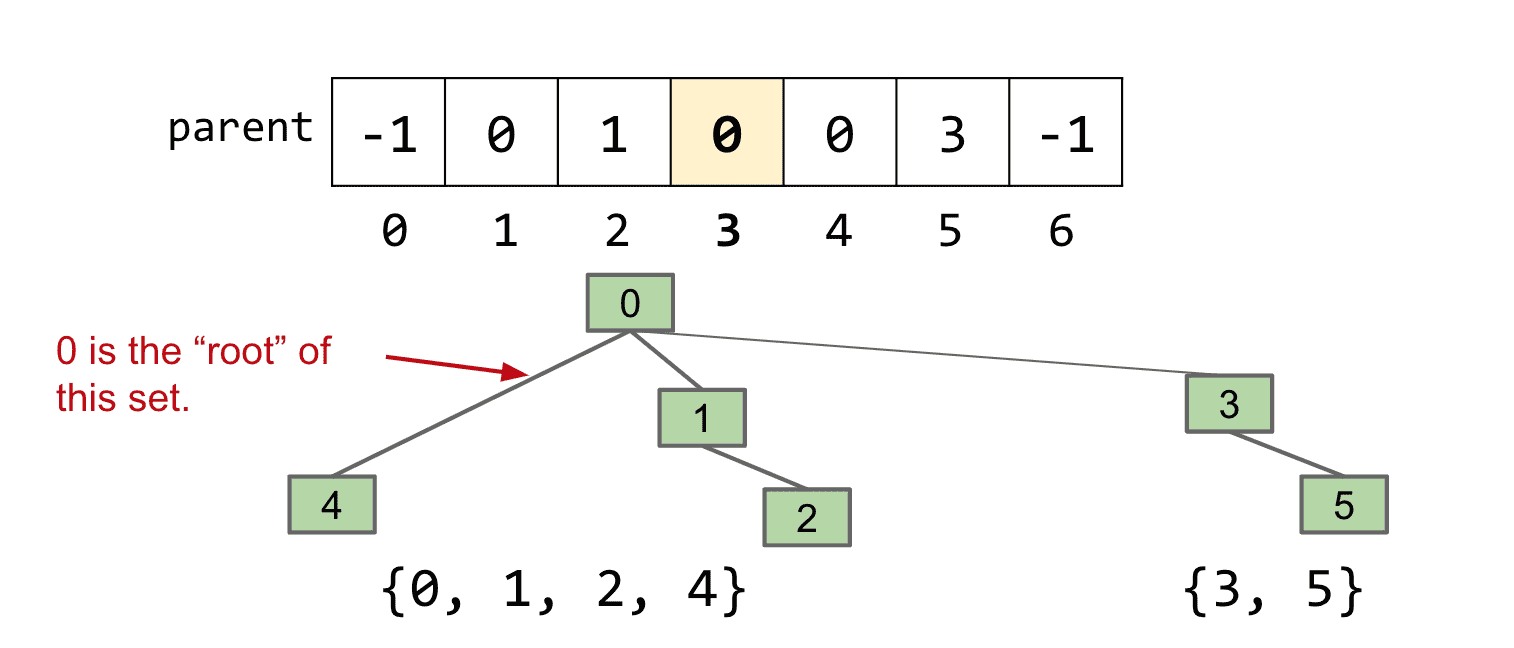
但是这么做还是会有问题:
在元素量足够大时,整个tree也会变得巨大
我们进行isConnected比较时是比较元素的root是不是相同的,所以tree很大的时候消耗的资源也很大
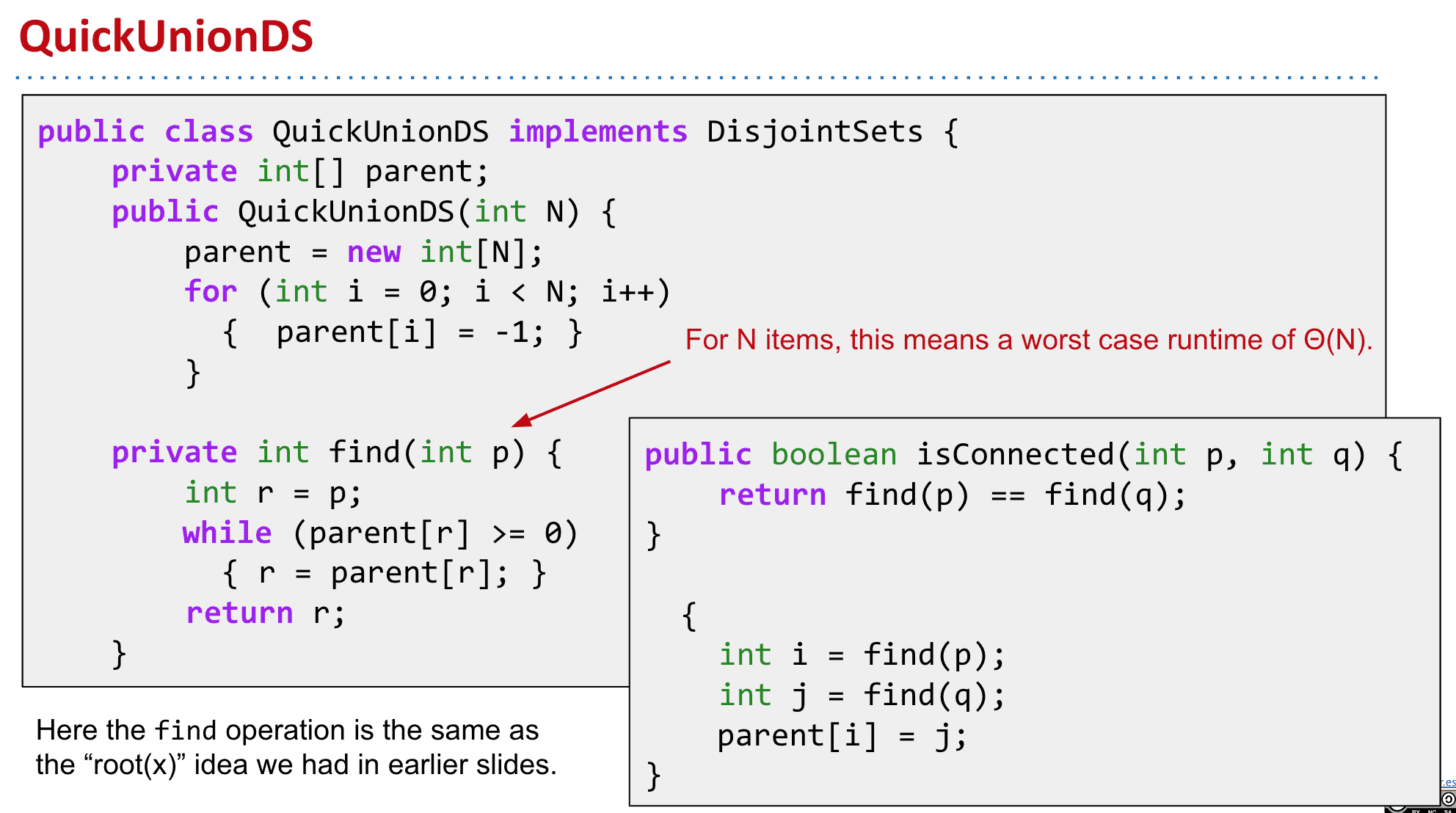
大概的实现
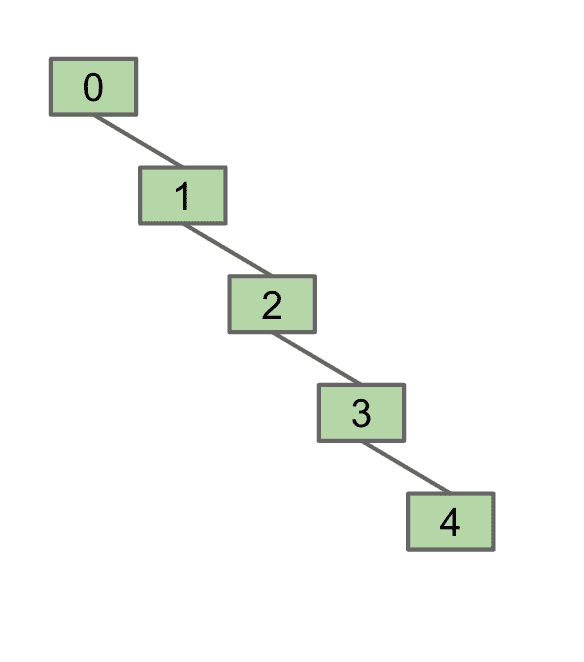
tree可能变得很巨大
Weighted Quick Union
上面说到了tree变得很高时资源消耗会很大,所以改为连接不同连接组件时,连接到根部
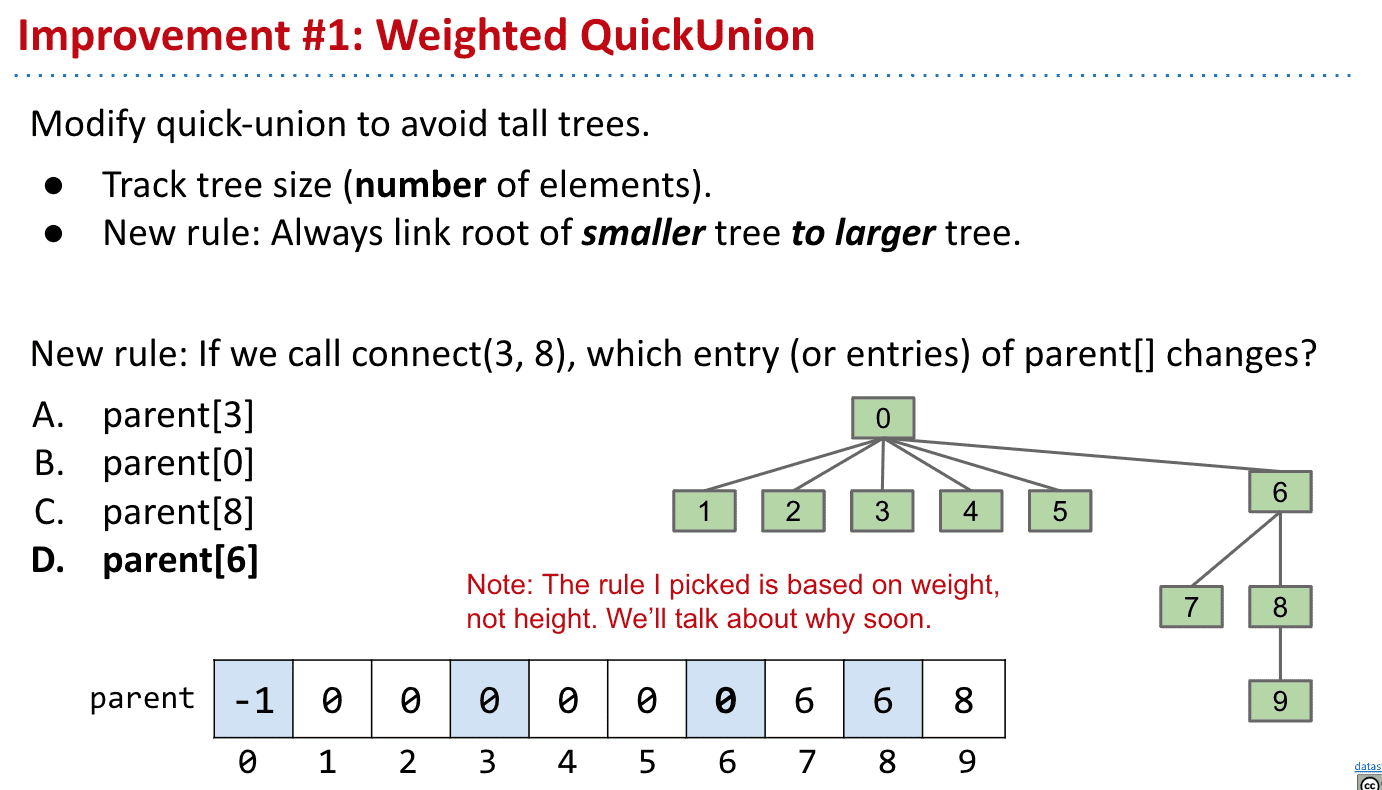
有两个需要注意的点
- 记录tree的大小
- 连接时把小的tree连接到大的tree的root
而记录大小也有两种办法
我们可以把根的存储数作为大小(负数代表是root)
或者我们可以另外用一个size数组来记录大小

小总结:
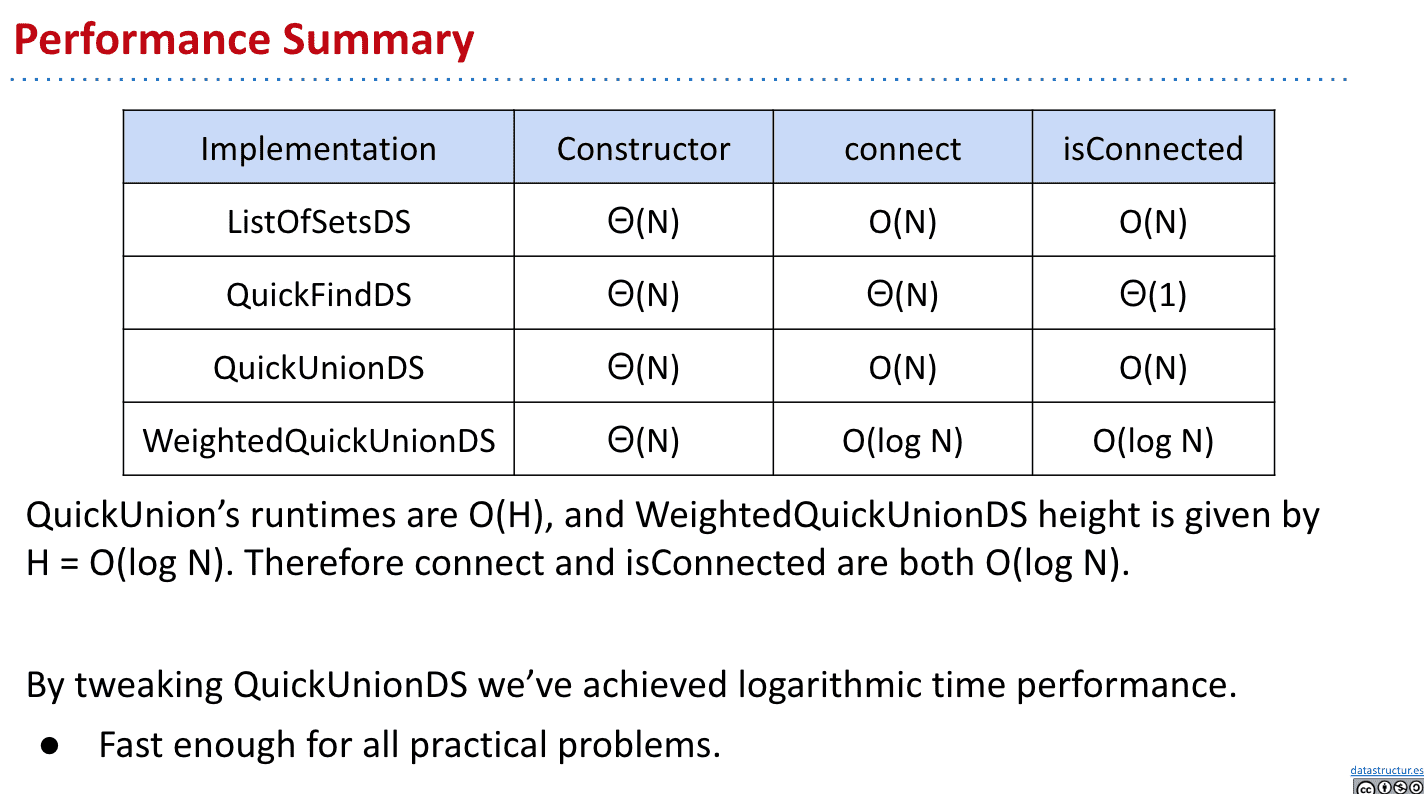
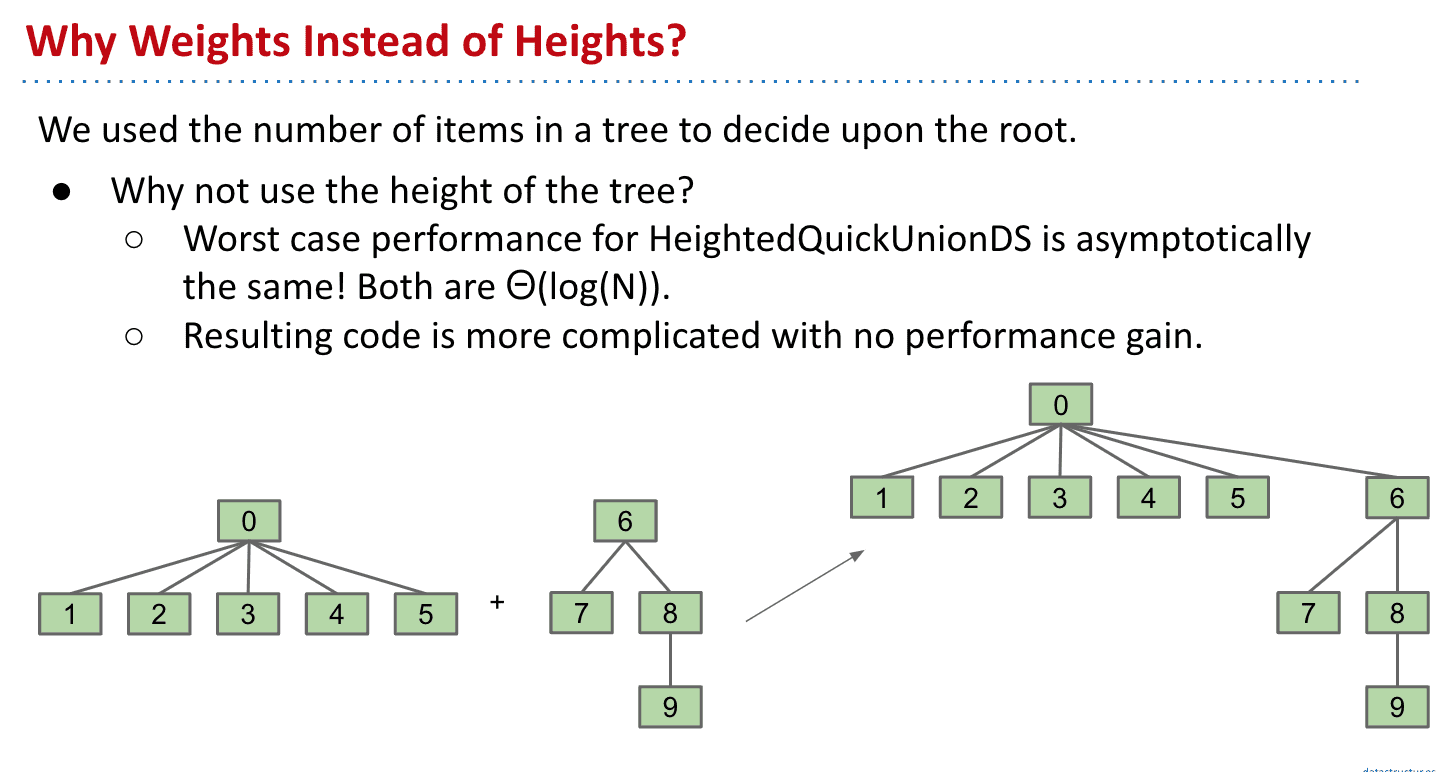
为什么不用heights作为size
Path Compression 路径压缩
是cs170的内容,只做了解

从简单但性能消耗大的实现→复杂但性能表现好的实现

渐进分析 part2
对于各种O的符号表示还不清楚,先跳过
但是有一点很明确,想知道运行效率啥的 没有捷径可走,不能一看到几个循环就说大概多少,因为程序里可能随便一行就影响运行效率很多
只有好好计算才呢得出结果

Recursion

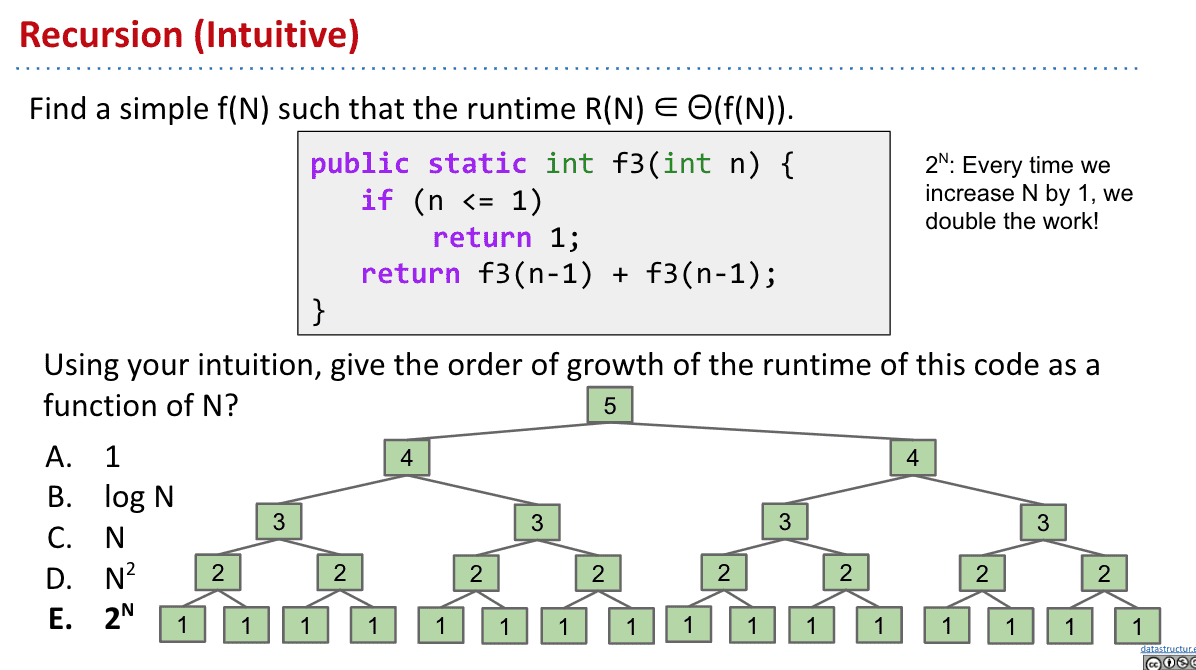
这种递归的运行时间其实观察就看出.每多一轮就是多一倍和一个root的1
所以省略1后就是
Binary Search 二分法检索
这个上CS50时撕电话本那里就很熟悉了,每次减半,

从一个一个找数字,变成了每次减半


相比一个一个找,在大量数量级下很省时间
Mergesort 归并排序
以前介绍过选择排序(selection sort)
第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾

这种方法很耗时,6个元素时36次操作,而64个元素时就要4096次操作了
所以引入了Mergesort
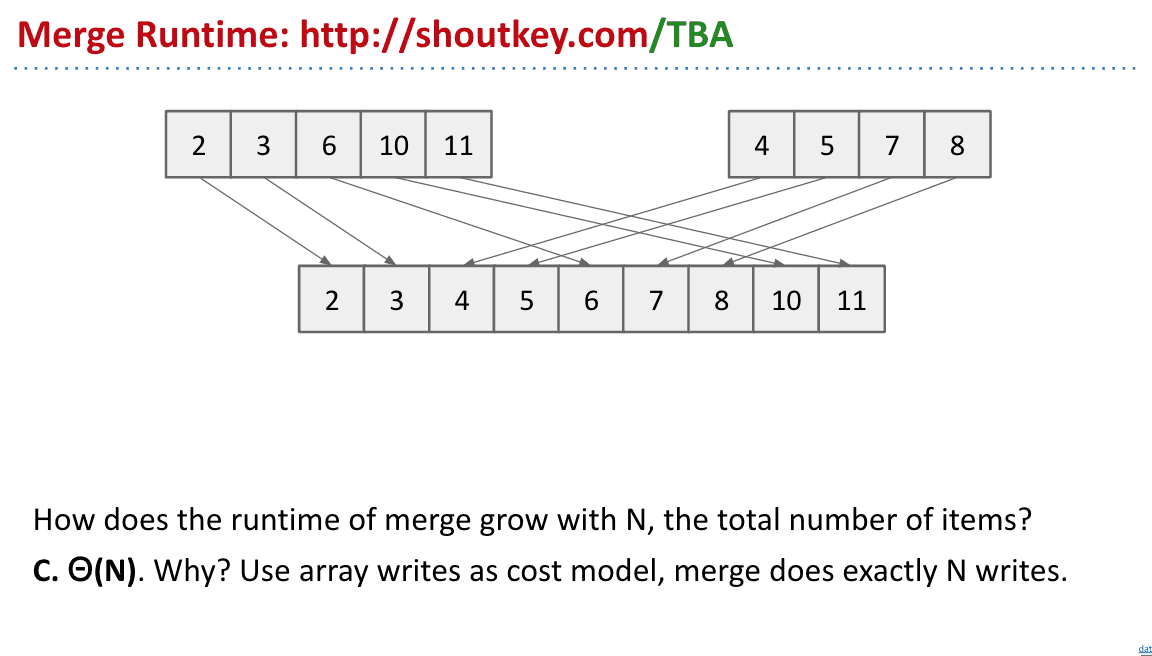
两边数组依次对比,把小的拿出来放入新的数组,这样操作次数就和元素本身一样
所以我们可以把selection sort拆成2半整理完后使用Merge

但是我们发现如果一直分下去的话,其实不需要selection sort

完全使用Mergesort后发现每次操作其实都是N次((N/2)*2=N)所以只需要次
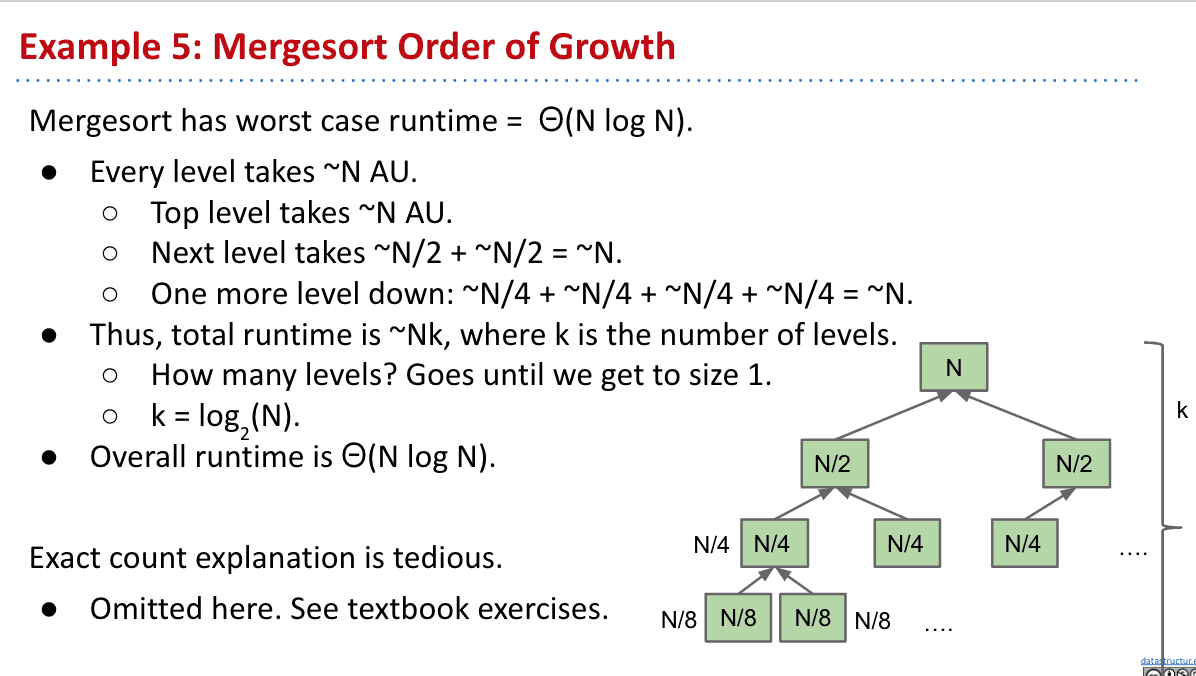

渐进分析总结
渐进分析时不能一样看出来的,没有捷径 只能好好计算
符号表达还需要好好学习(video)
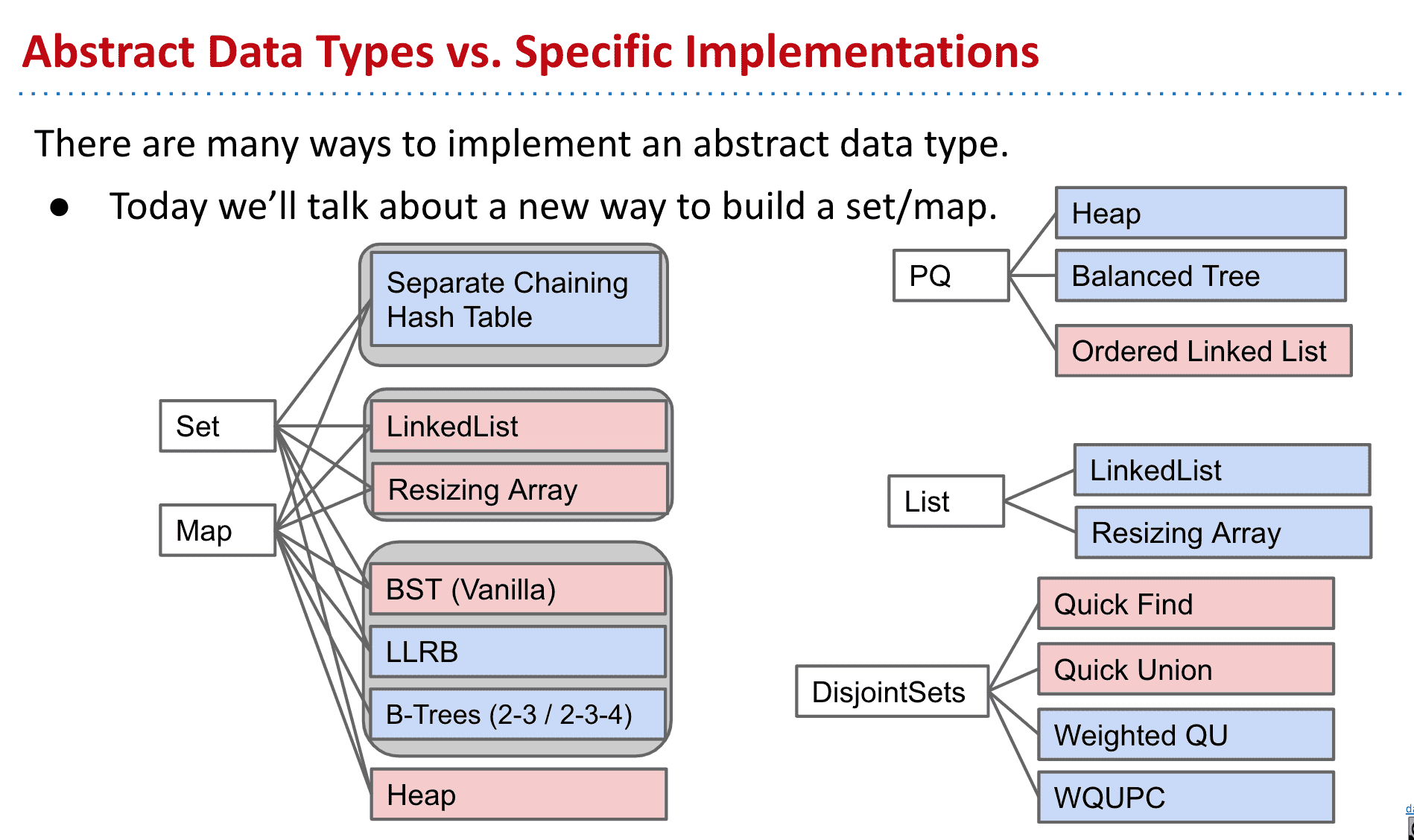
抽象数据类型 Abstract Data Types
一个抽象数据类型(ADT)只由其操作定义,而不是由其实现定义的
比如像DIsjoinSets有很多种实现方式,当我们谈到抽象数据类型时其实并不关心它底层的实现,而只关心它的API
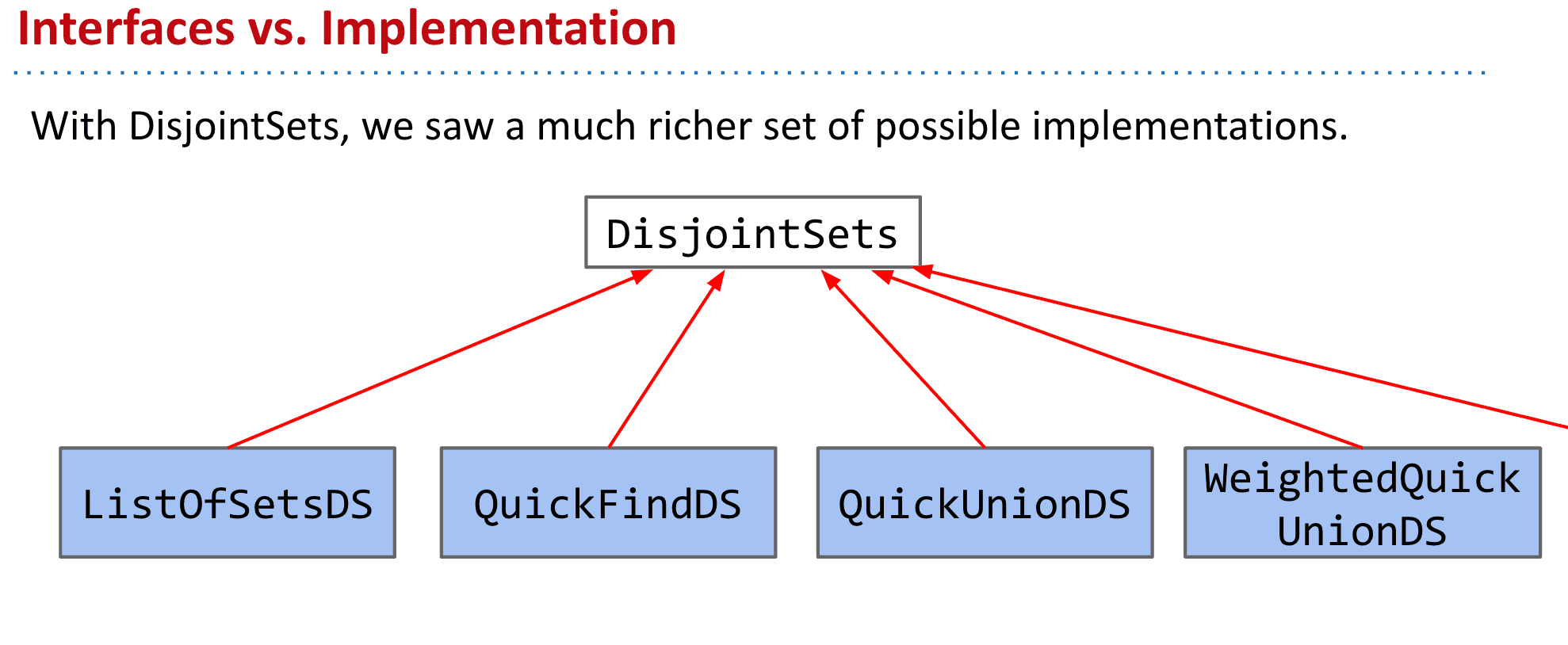

我们只关心它的API
集合有很多种类型,比如Map


使用Map记录文本里某个单词出现的次数
二叉搜索树 Binary Search Trees
CS里最重要的数据结构之一
制造一个二叉搜索树
假设我们有一个按照顺序排列的LinkList,
可以发现加东西和查它是否存在都很耗时(没有利用到它按顺序的优势)
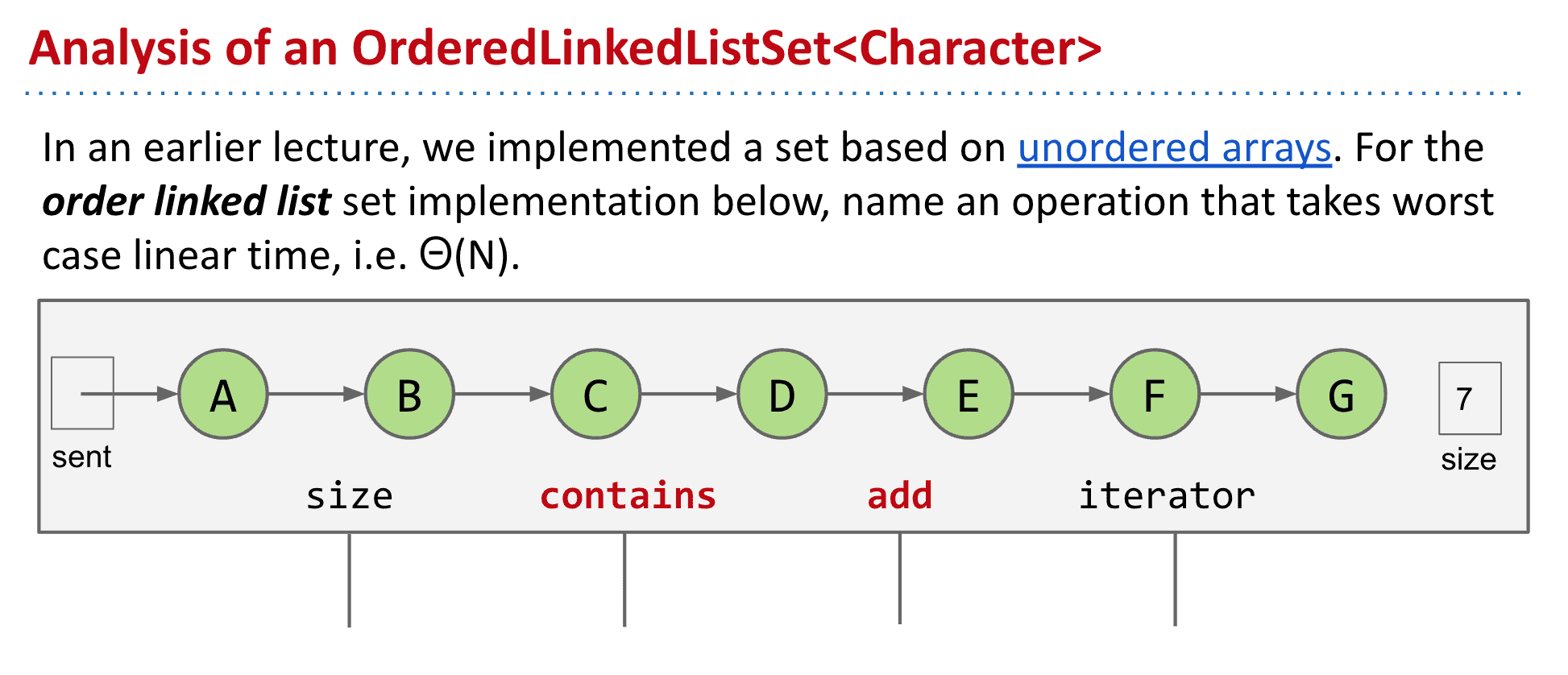
(想法)我们可以给节点添加随机的指向其他节点的结构,性能就会好不少(真实存在的结构,叫做Skip list在有序链表的基础上增加了“跳跃”的功能)
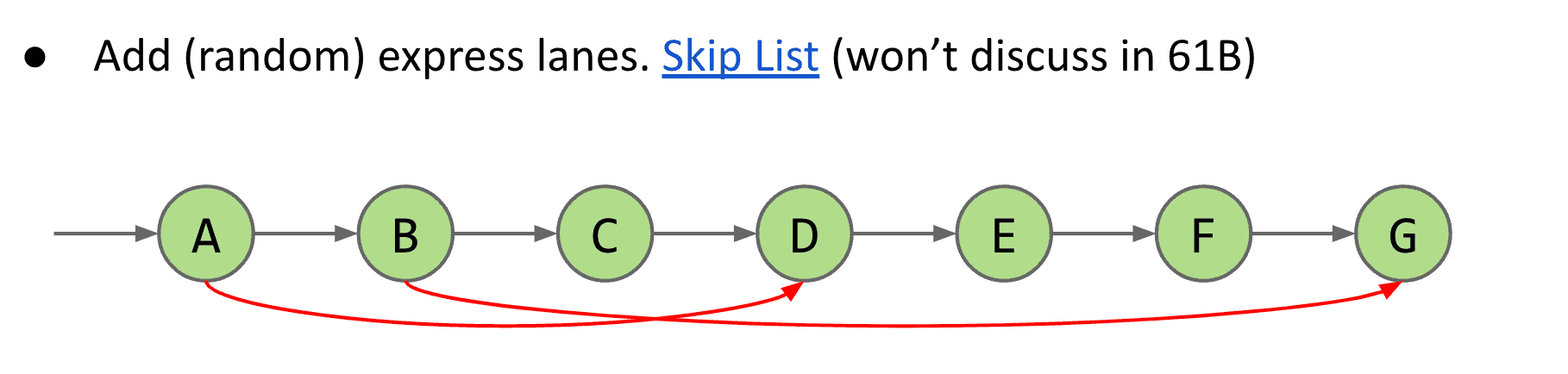
仅仅是个想法
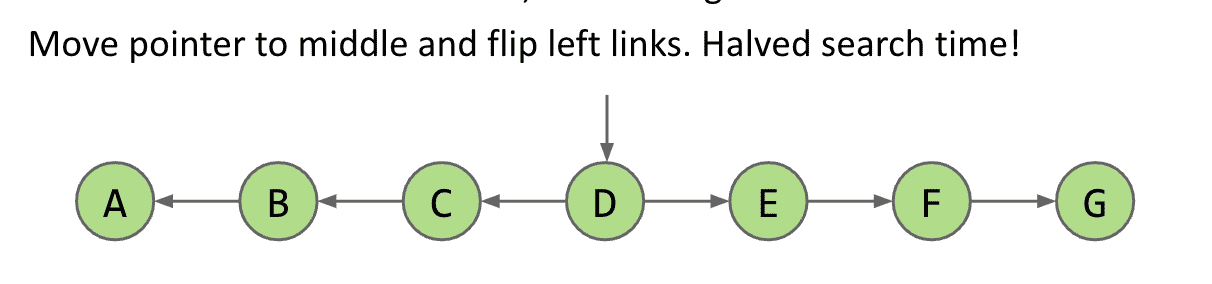
我们可以把指针放在中间然后link指向两边,这样我们的效率就会加倍

进一步提升的话,我们可以中间指向两边的中间,再进一步的话就诞生了二叉树
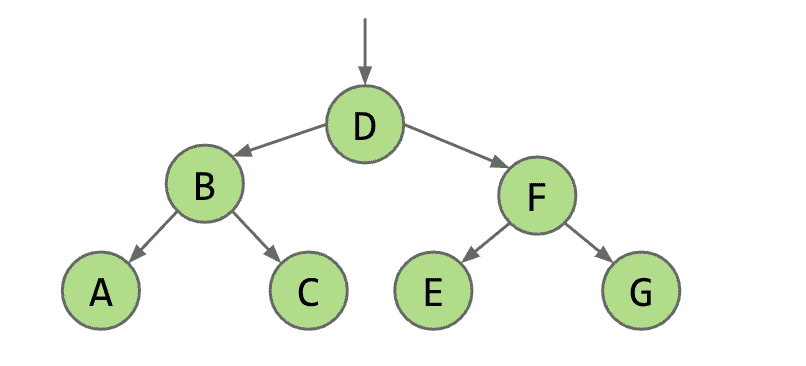
二叉树的结构
成功“制造”出了二叉树
BST的定义
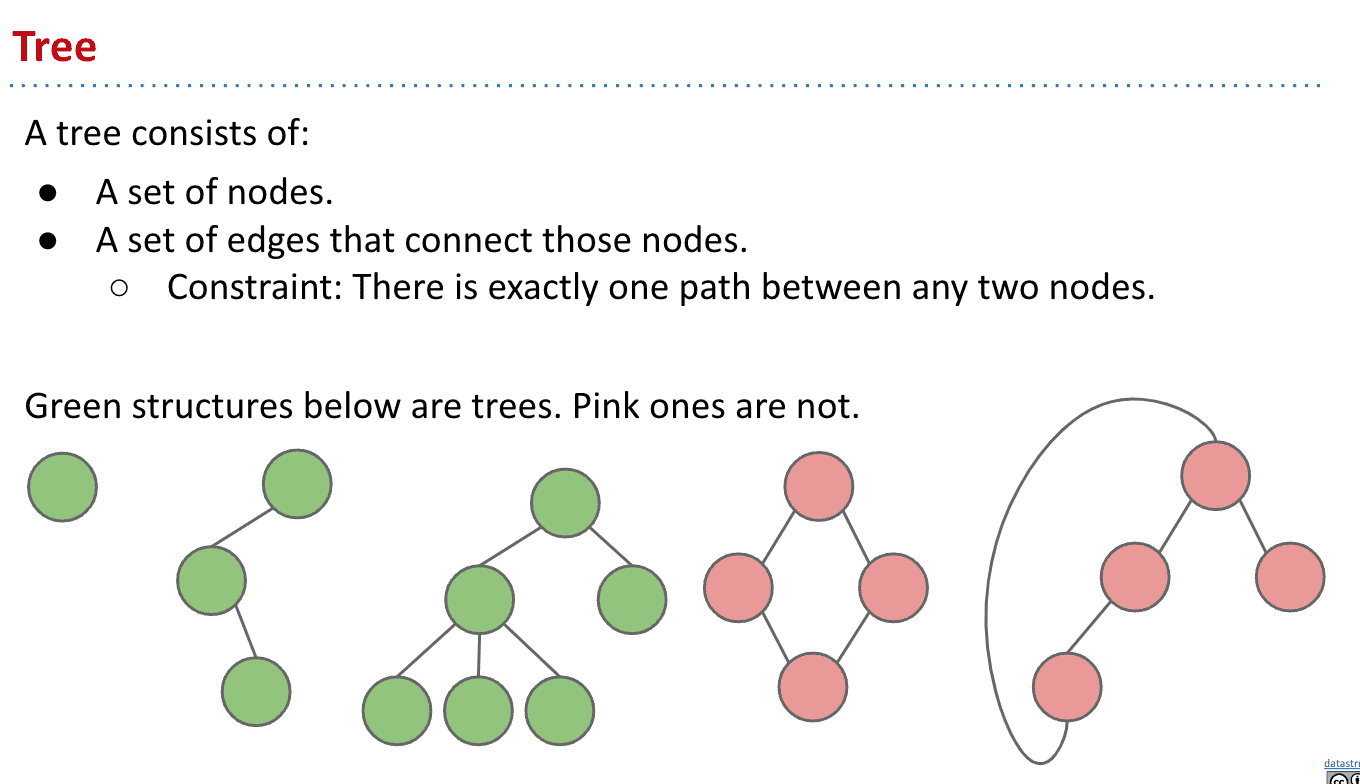
首先什么是Tree
红色那样有两条路从上到下的就不是tree
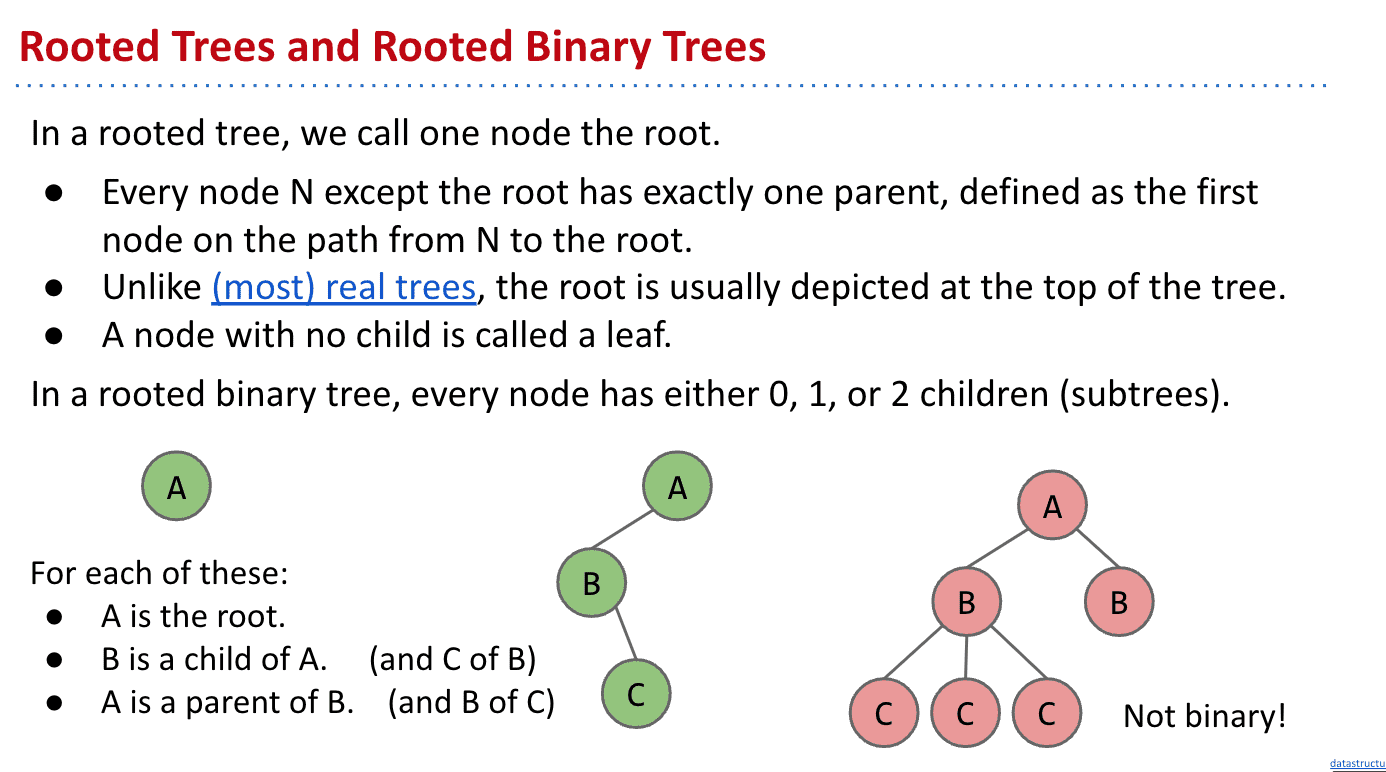
有根的树
指我们指定了一个节点(node)为根,而除了它以外的节点都有父级
二叉树
一个节点只有0、1、2个子节点
二叉搜索树
要求左边必须小于右边
不能有相同大小和重复的节点
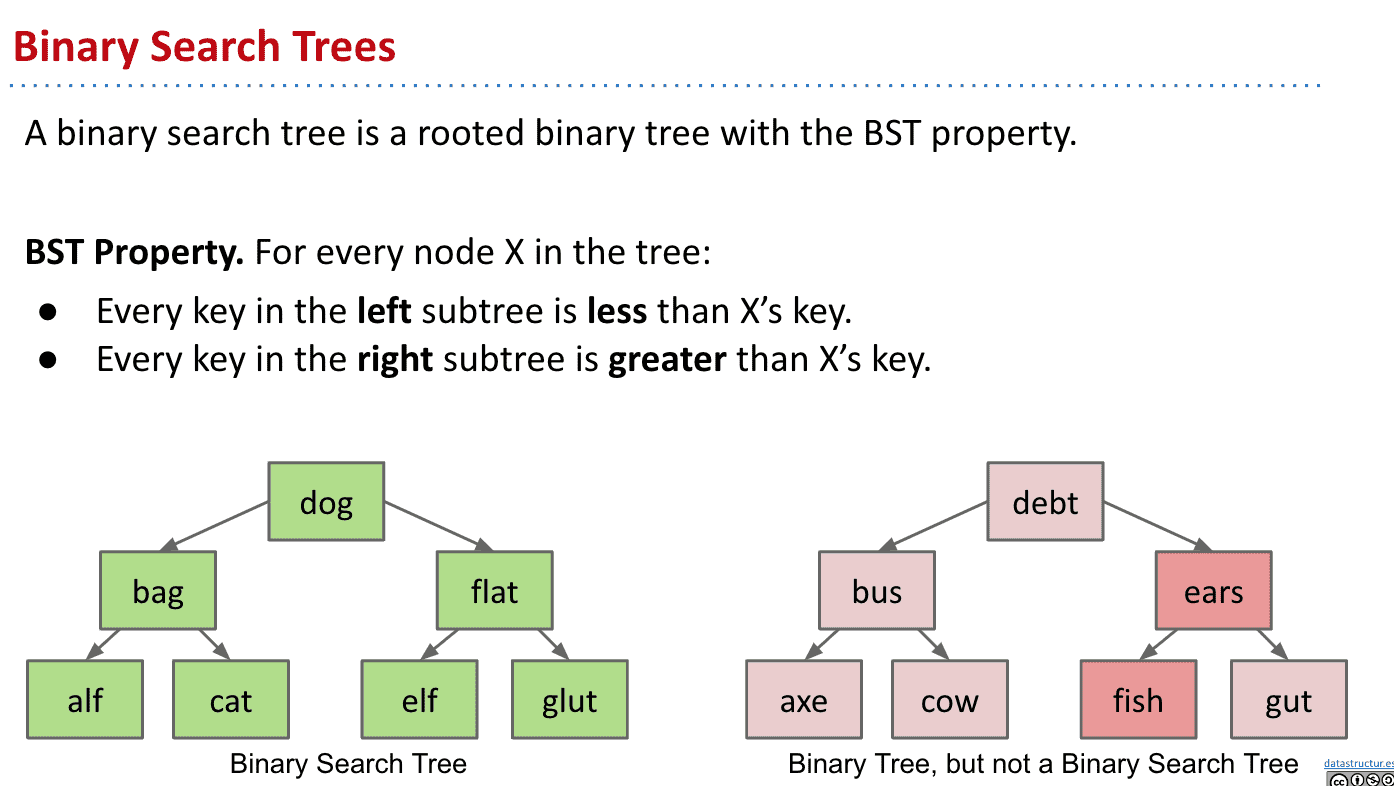

BST操作
搜索 search
比较搜索值searchKey就行了,
最糟糕的情况下也只需要Θ(log N)
超级超级快
在每次操作1微秒的情况下,可以在一秒钟内从大小为的tree上找到想要的东西
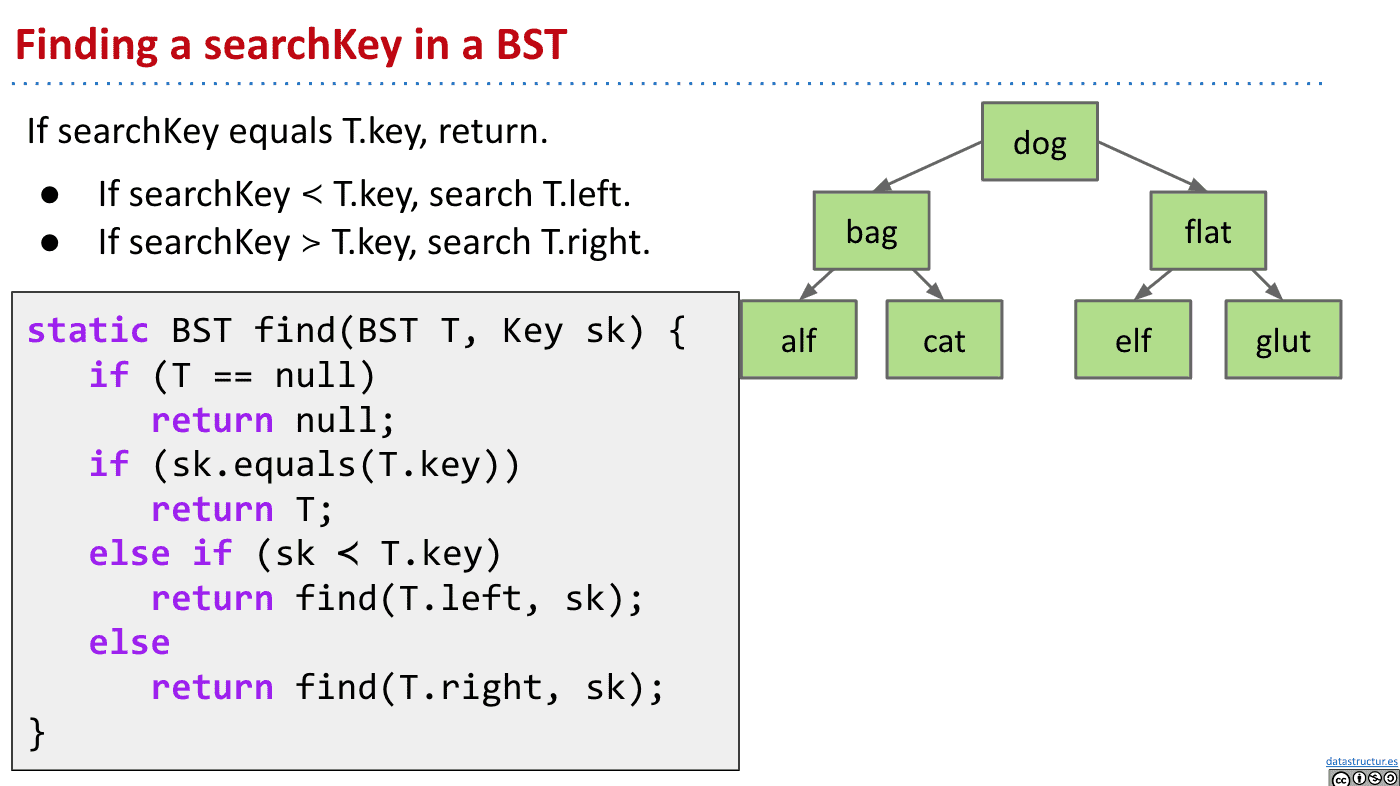
注意接下来的代码都是描述性的,非真实代码
插入 insert
代码解读:
首先传入tree和要插入的东西的key,如果tree不存在就返回一颗新tree,然后不断深入迭代
只有树是空的和node已经存在才不用递归
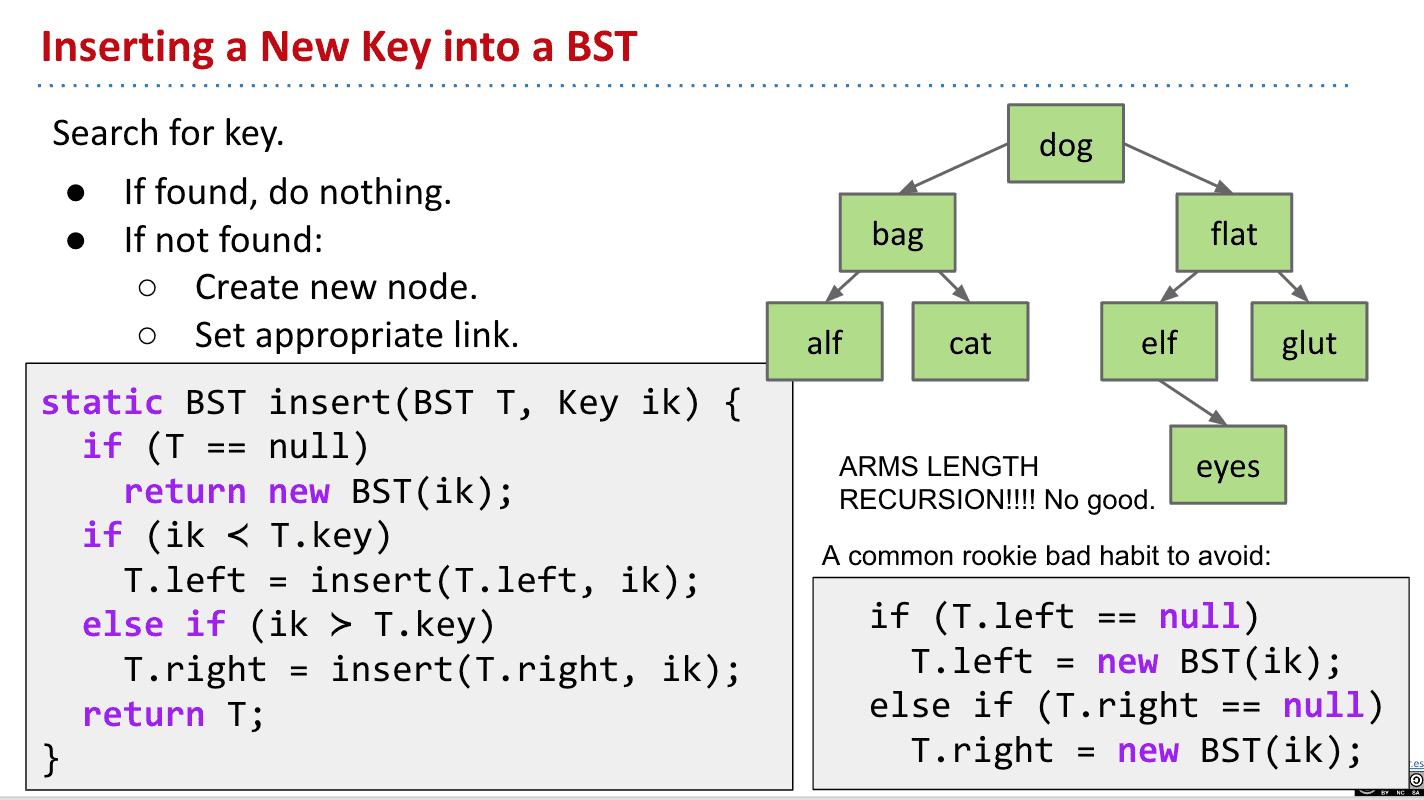
BST代表tree、 key代表searchKey
右下角的是错误的代码示范
删除 Delete
删除有三种情况
没有子节点的直接删除连接就行
有1个子节点的删除🔗再把它的父节点指向子节点
删除有2个子节点的比较复杂
但只要选择删除节点的前任和继任来作为新的节点就好了
比如要删除dog那它前面一个是cat后面一个是elf,就都可以作为新的节点代替dog
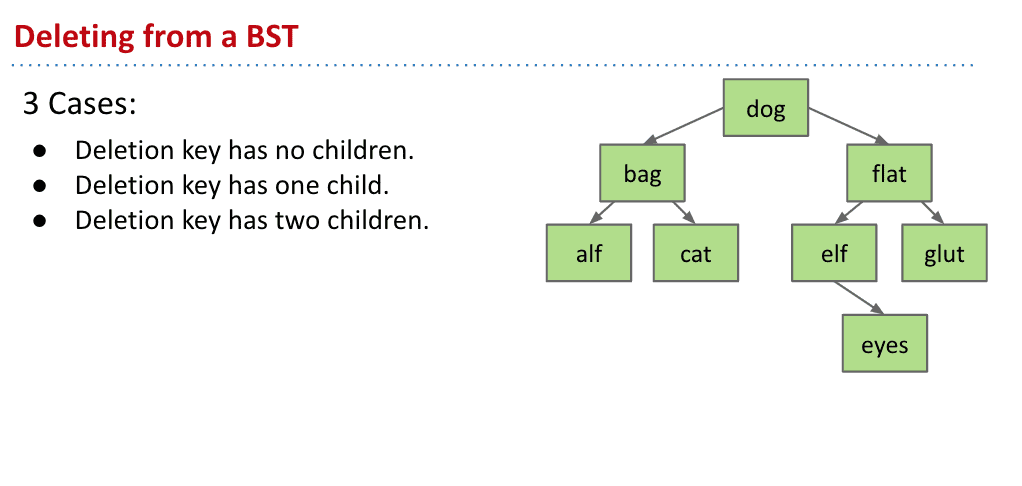
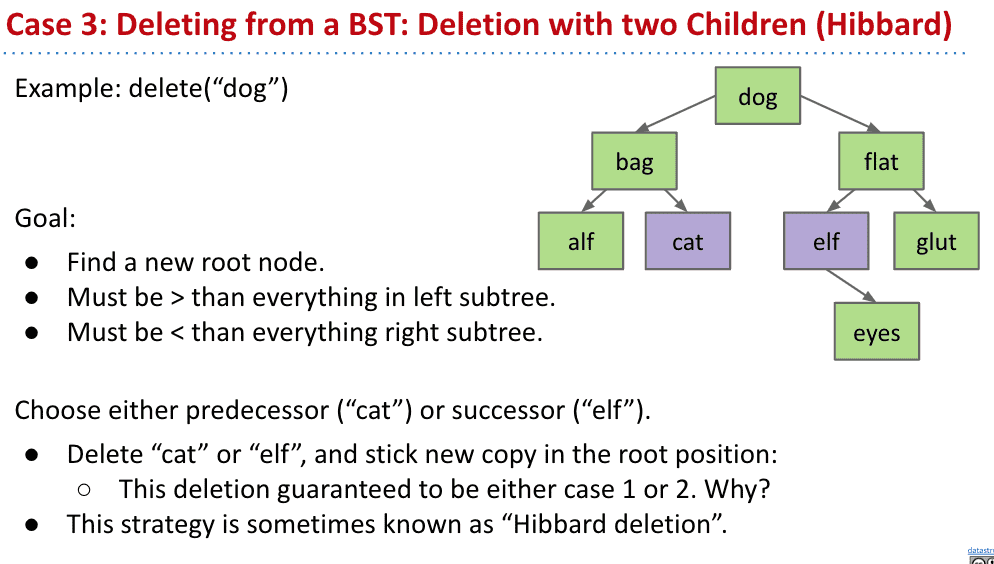
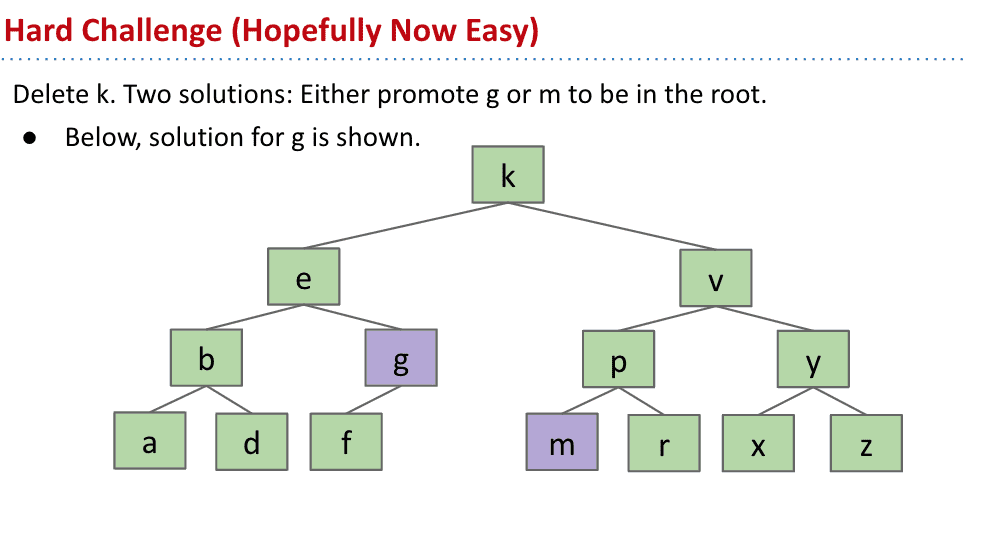
删除前
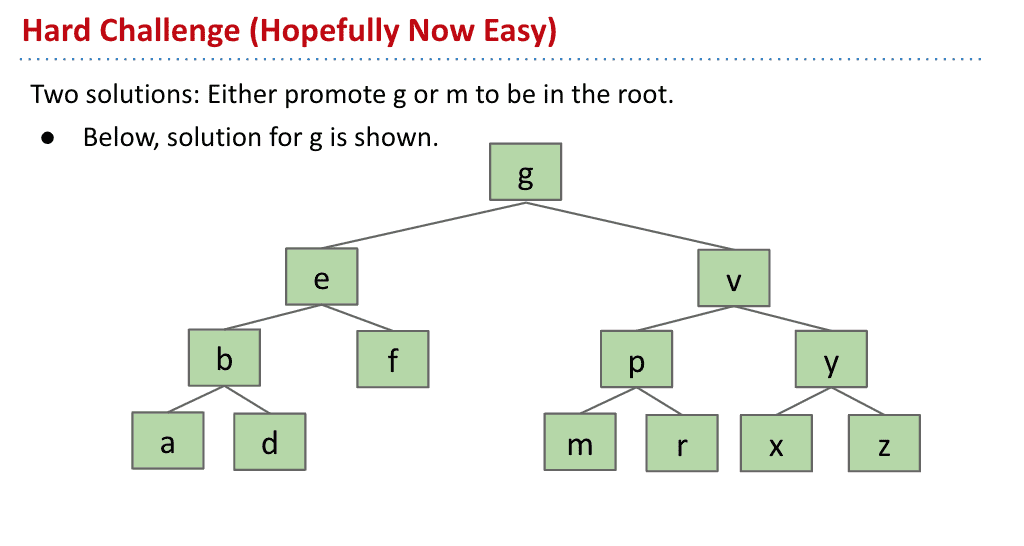
删除后
上图我们要删除k节点,而他的前一个是g后一个是m,所以都可以作为新的root
假如选择g作为新节点,那么g以前的父节点e指向g以前的子节点f就可以了,而g代替k
删除操作要记住二叉树的右边比左边大
如果想要用BST实现Maps,只需要在节点里加上存储的值就行了,当然缺点是排序和比如显示所有为1的节点必须全部过一遍
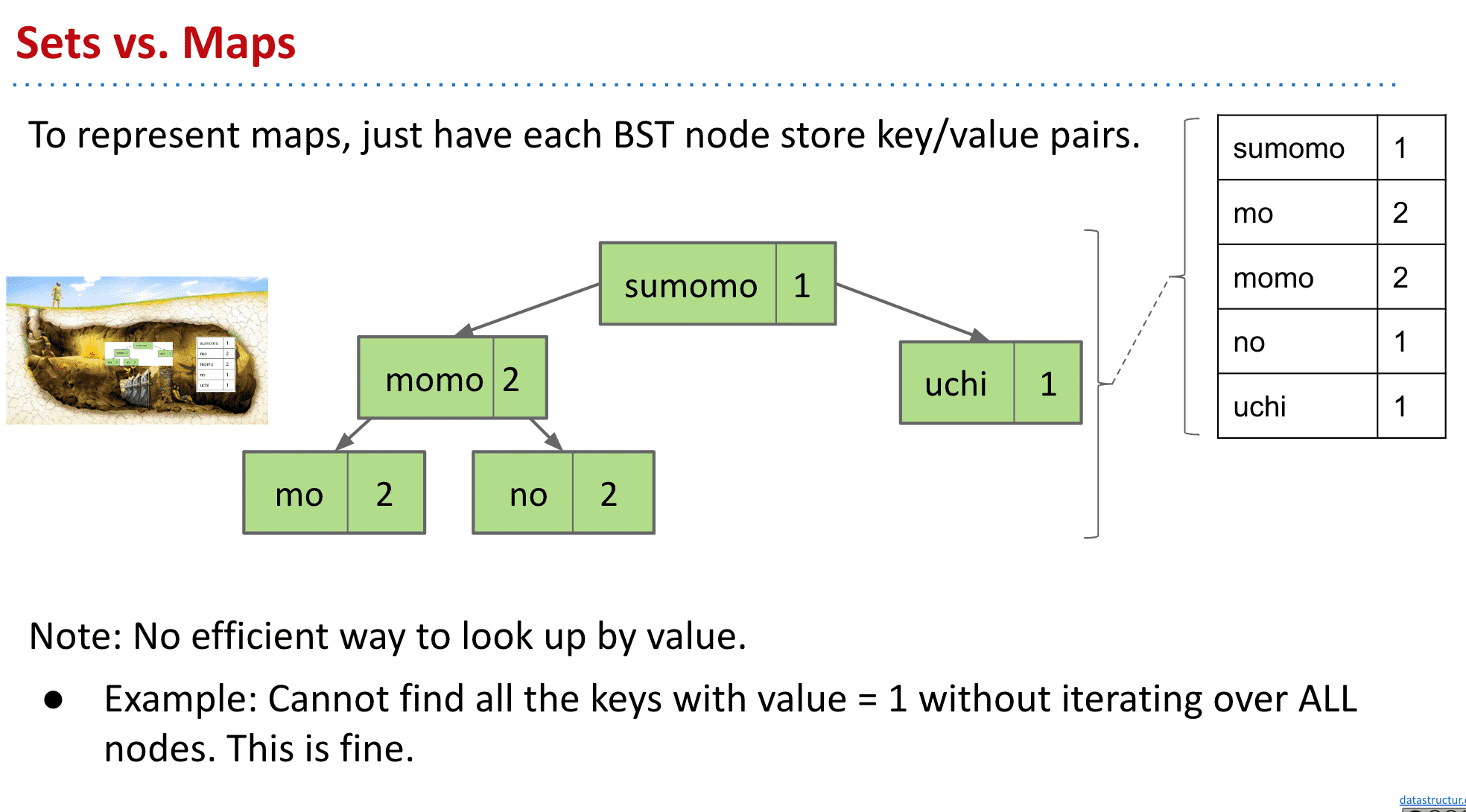
naked recursion和arms length base cases(recursion)搞不清楚
真正做的时候可能会清楚吧

Week 7
Θ(N)一般被用来表示最坏的情况(或者作为一个上限使用),O(N)一般表示最高(小于等于)的情况
可以看Big-O备忘单来看不同结构的运行时间
BST的Height和Depth
下面介绍了height和depth的概念,depth就是某个节点到根部的距离
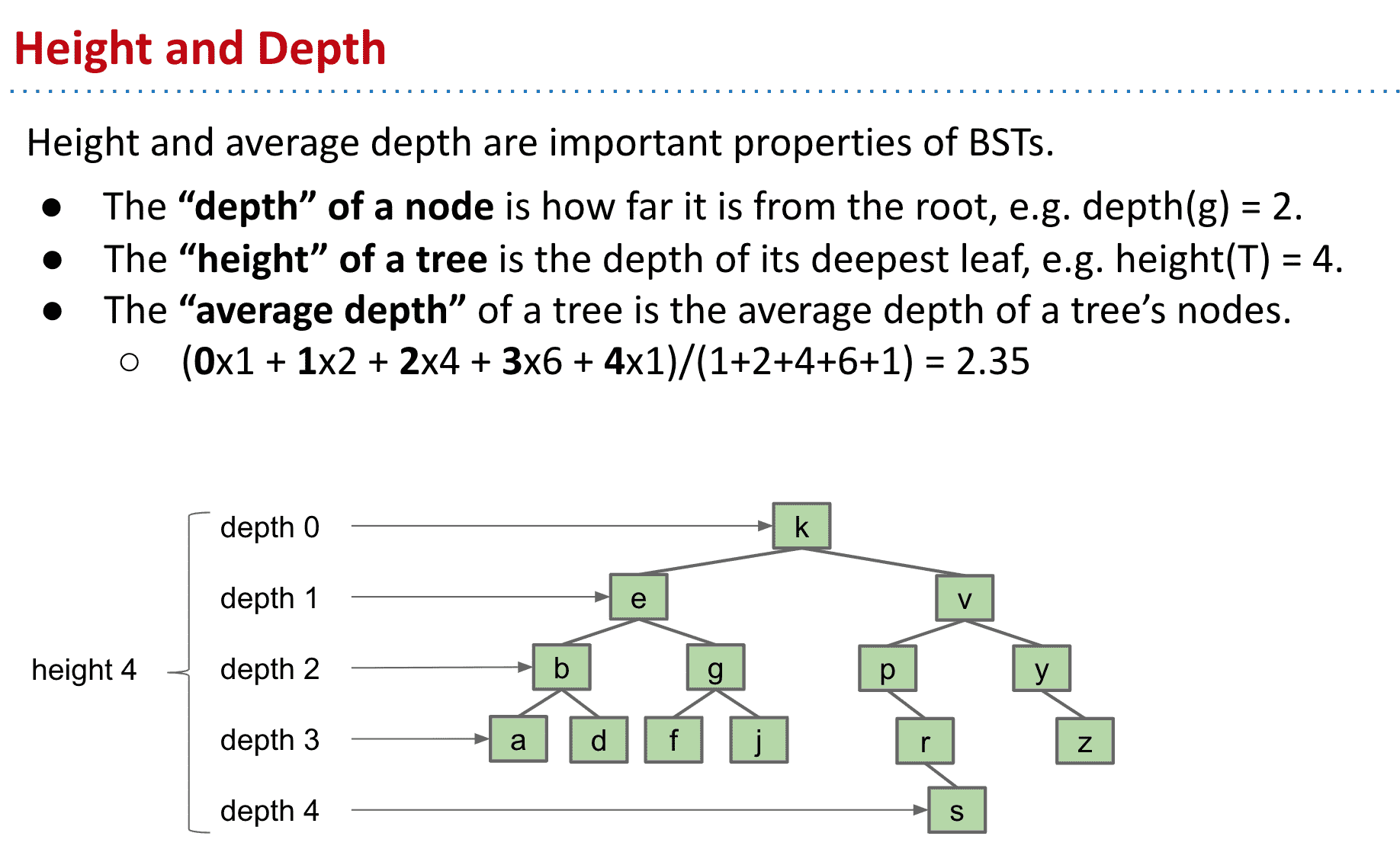

根据操作顺序不同生成的tree也会不同
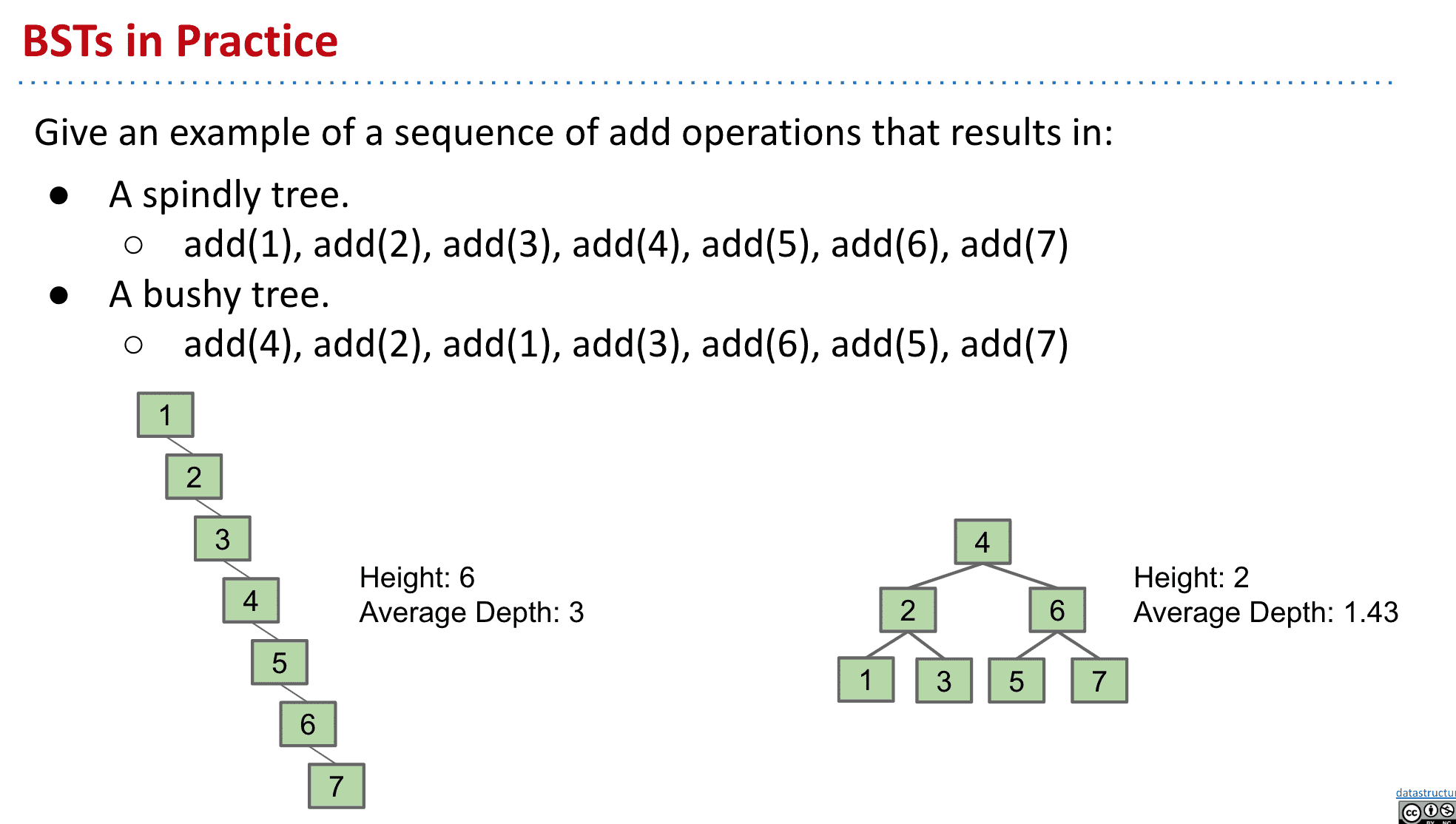
如果有个随机操作产生的BST,可以看出它会更bushy而不是spindly(所以更有利于性能)
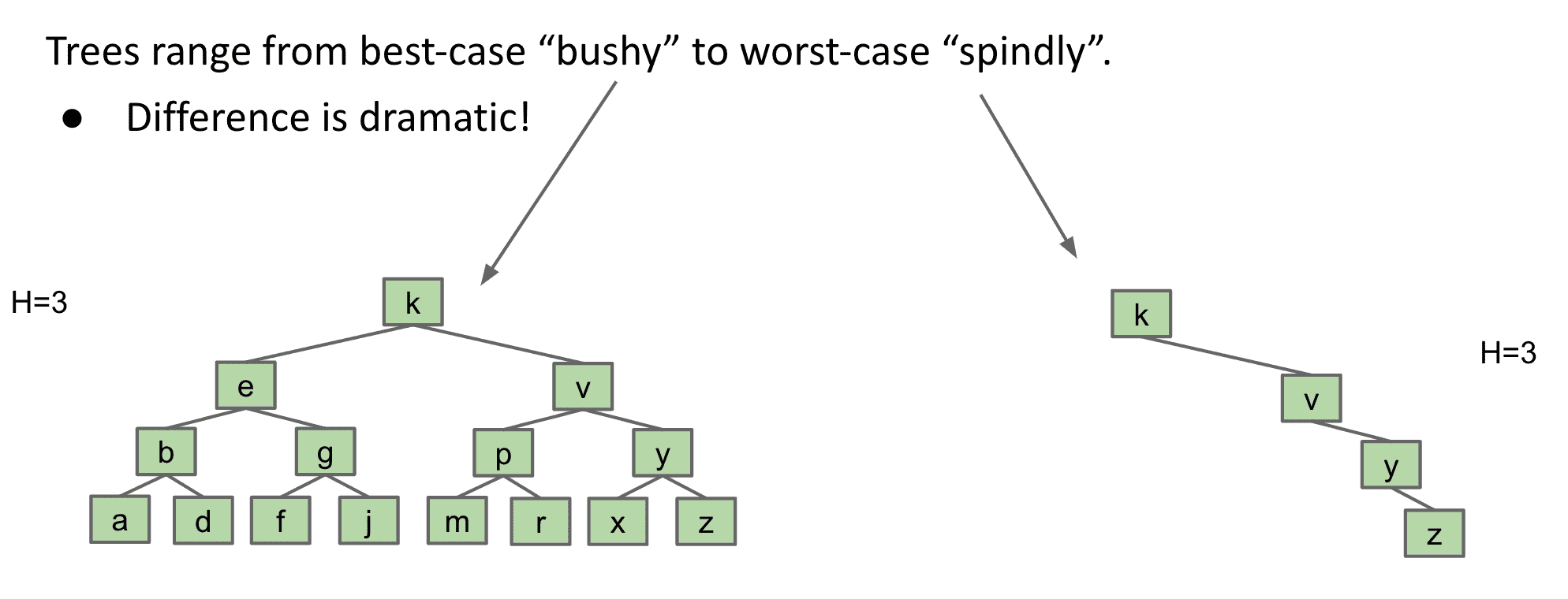

在现实中因为数据随着时间产生,可能导致更spindly的tree
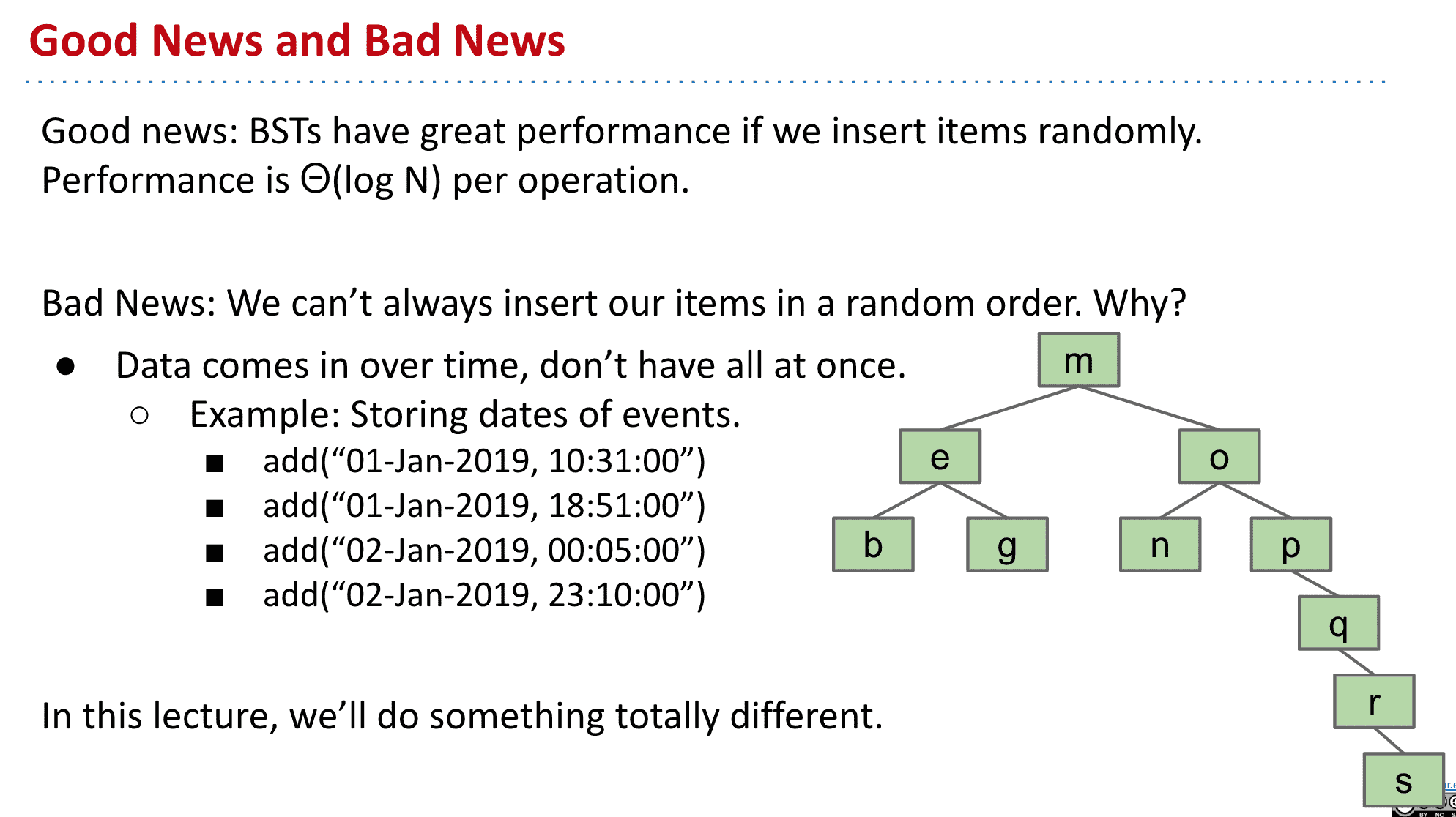
B树 B-tree
B树适用于读写相对大的数据块的存储系统,例如磁盘。B树减少定位记录时所经历的中间过程,从而加快存取速度
基本上就是一个拥有2个以上节点和一个节点可以存多个item的BST,并且会自动平衡 所以可以理解为Balance Tree
B树介绍
为了避免tree变得不平衡,我们可以设想在BST上一个节点加上多个值
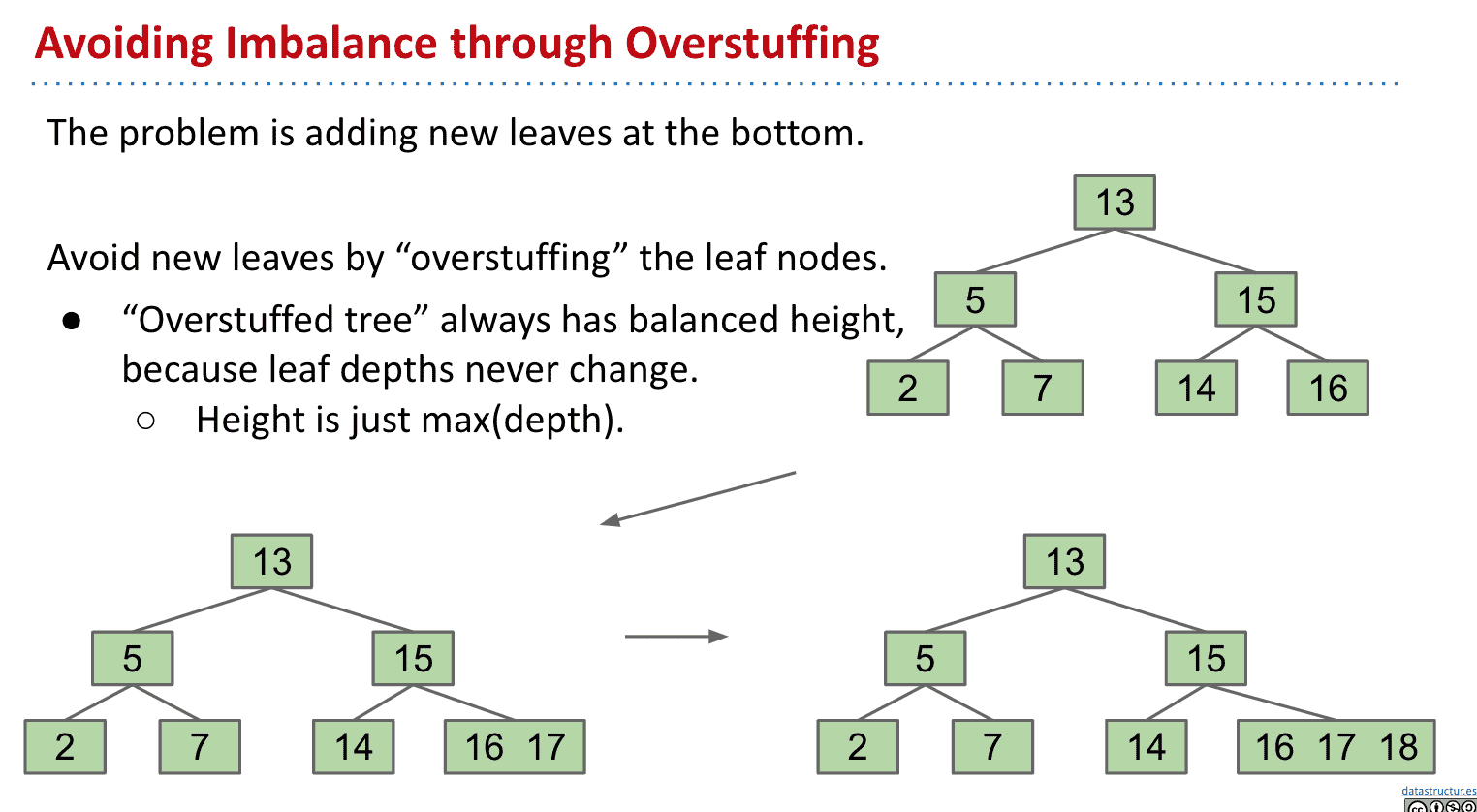
查找时只需要把塞了多个值的一个节点当成list之类的就行了
不过再加入更多值后,和BST类似的优点也没了
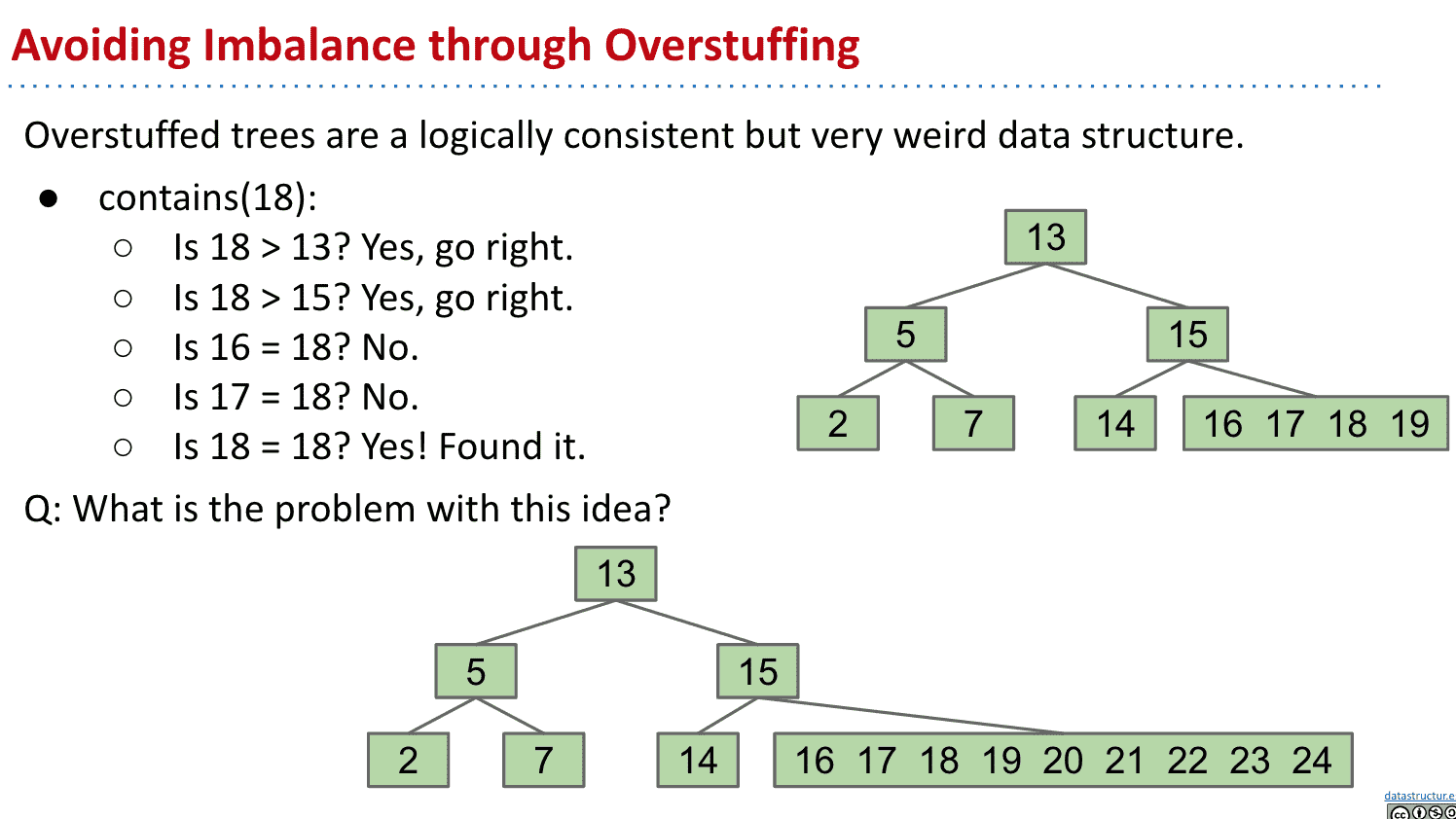
所以可以将超过限制(limit)数量的节点中的值向上移动
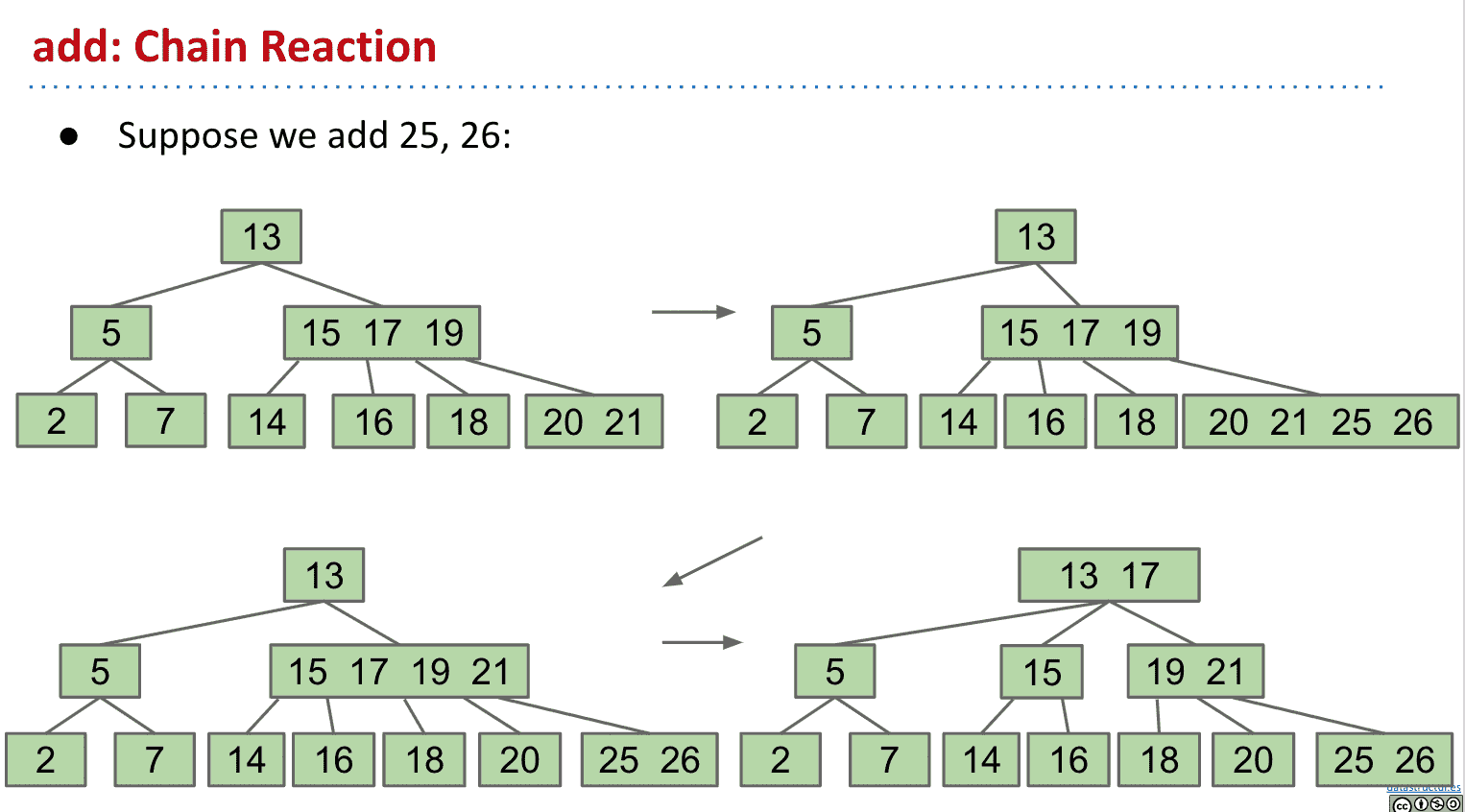
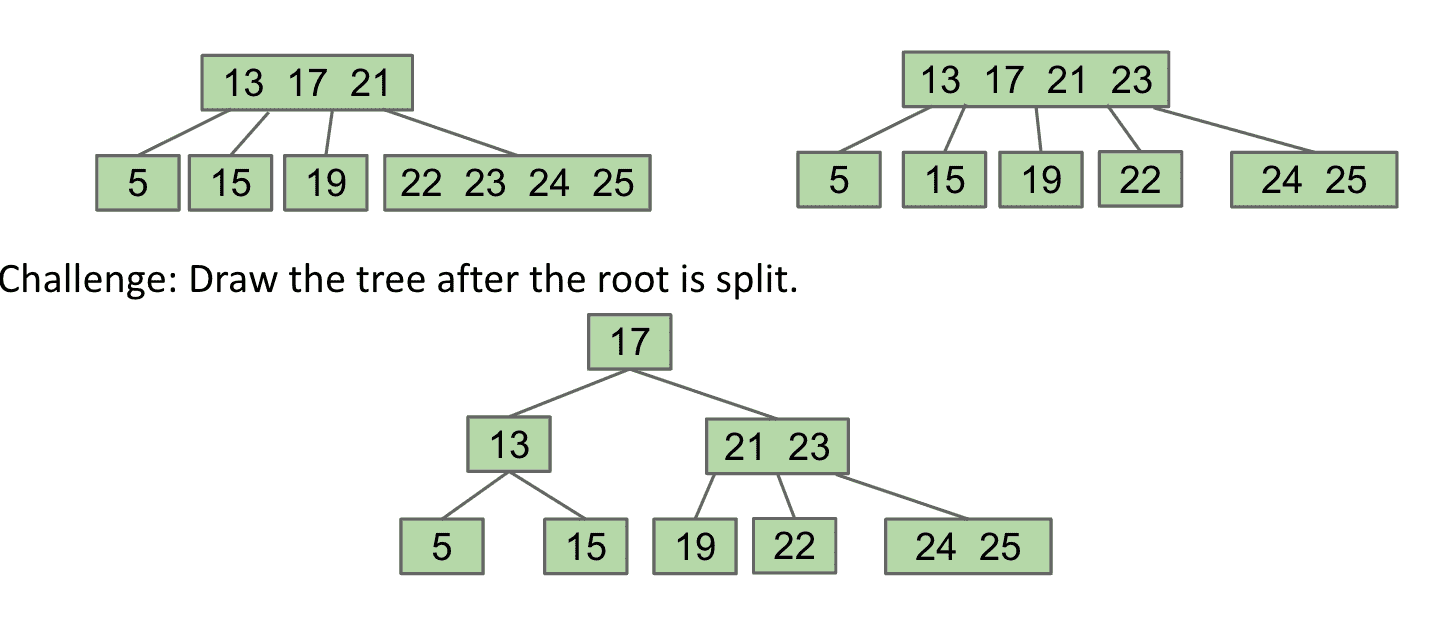
如果我们分裂根节点的话,就相当于其他节点向下推了一层,分裂子节点的话高度不变
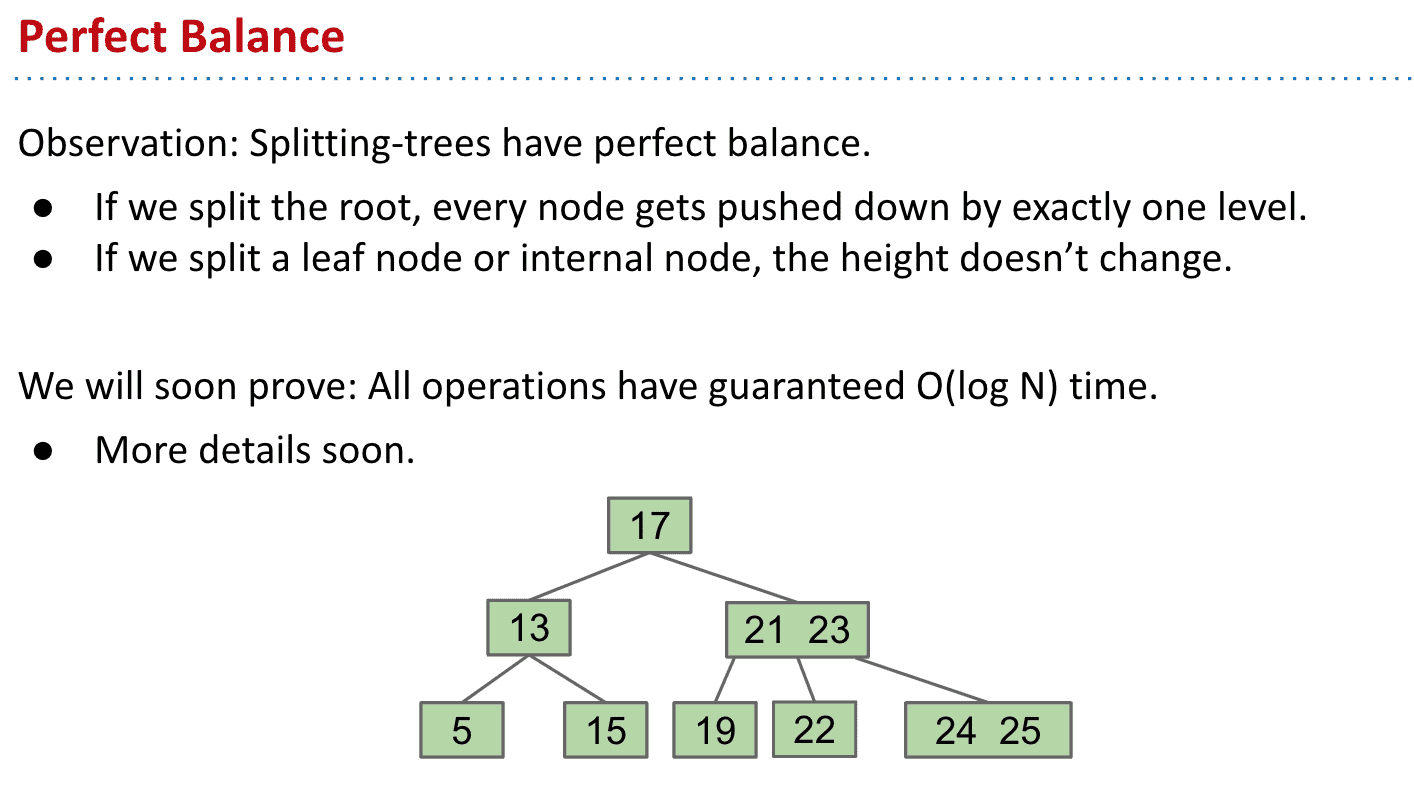
一个限制为3(一个节点最多3个item)的B树可能被叫2-3-4或者2-4 trees,代表有2、3、4个子节点

B树命名
限制可以自由设置,比如一个节点最多三个数,多了就向上传递
(在数据库中这个限制L可能被设定的很大比如超过一百)
如果限制为3,一个节点可以有最多3个item,4个子节点(注意3个数字之间可以插4个子节点)
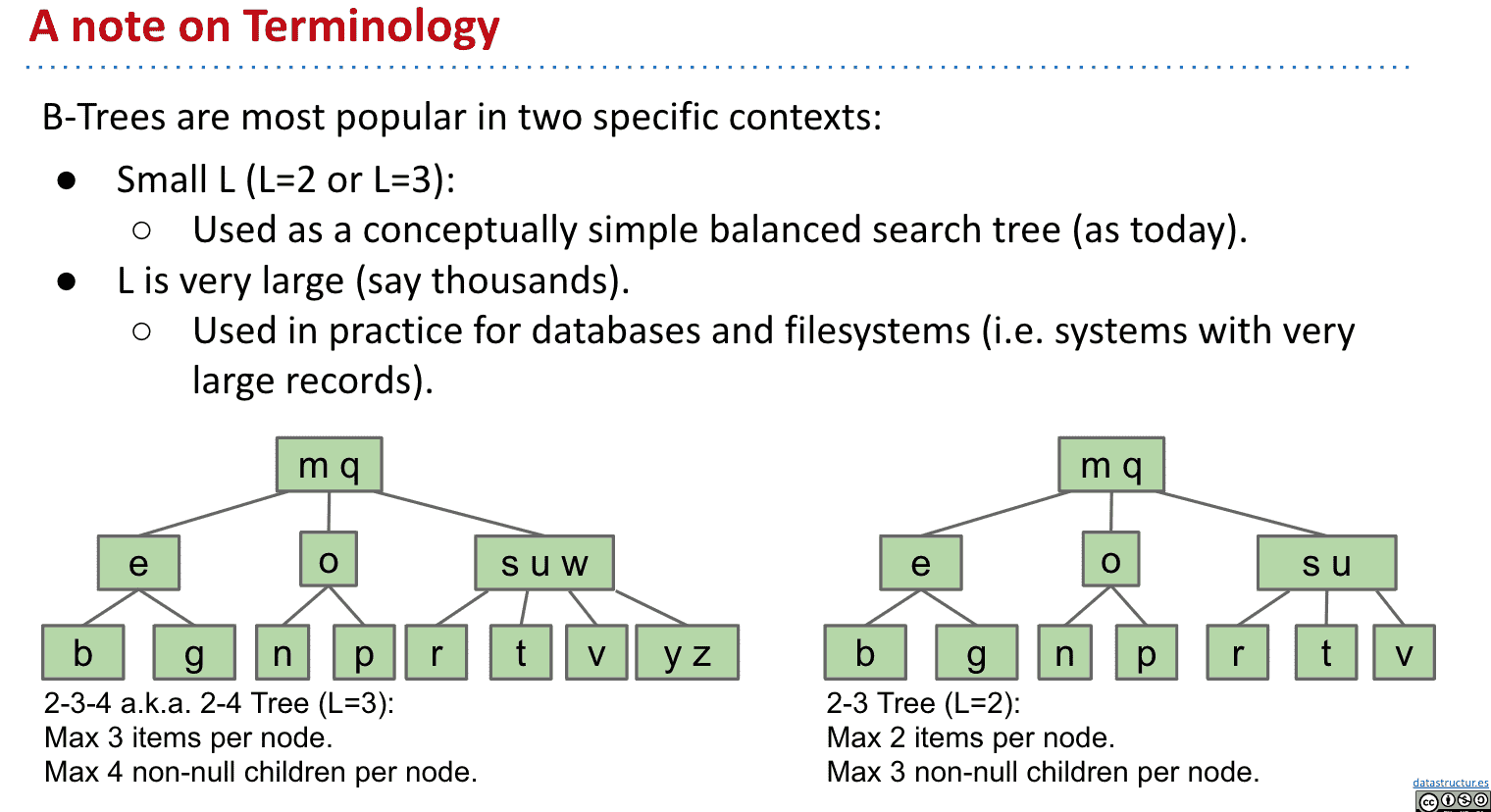
根据操作顺序的不同,我们得到的tree高度可能也不同,可以看出同样的高度最好和最差的容纳的item差了2倍多
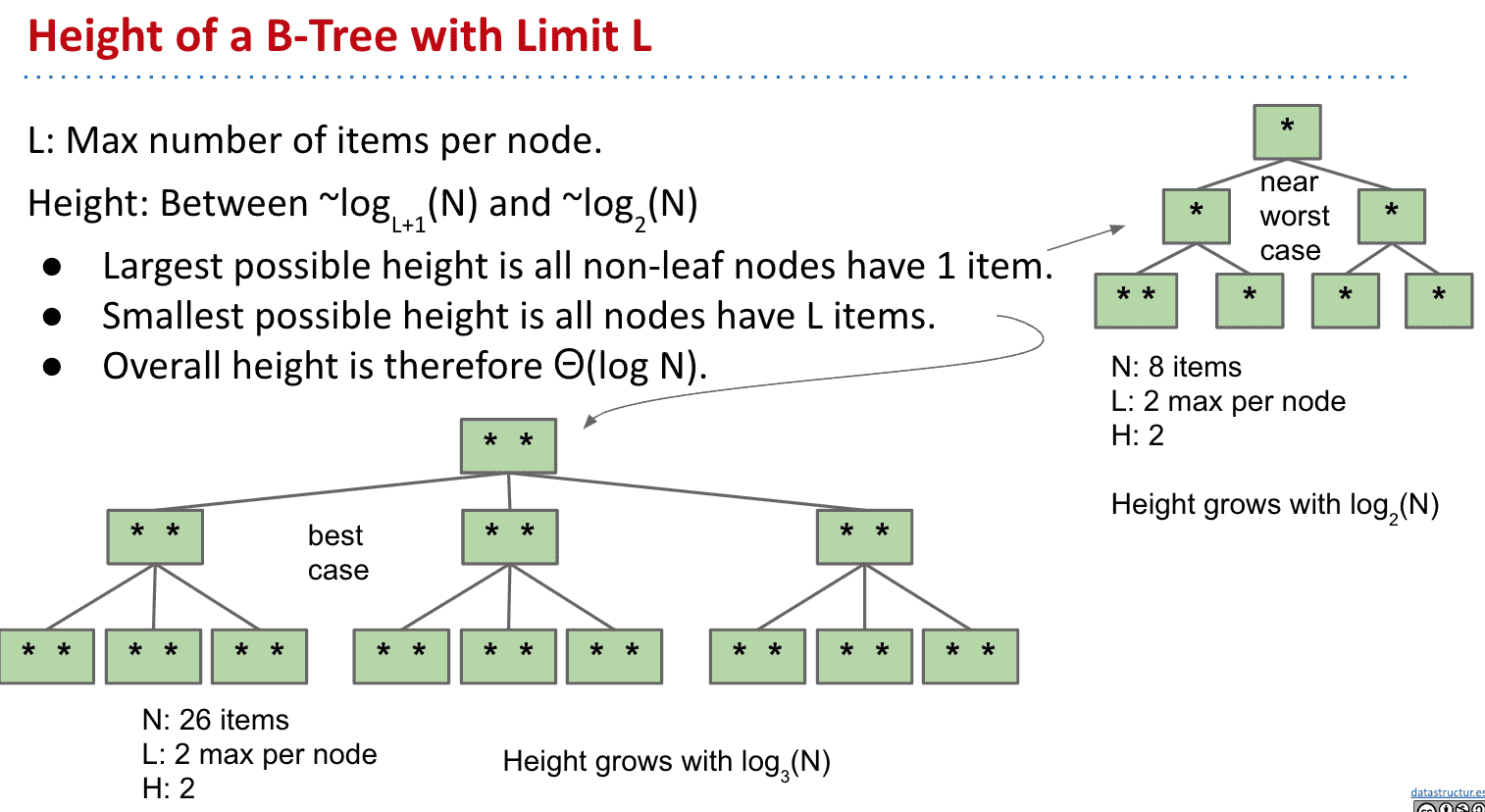
同样的高度不同的item数量
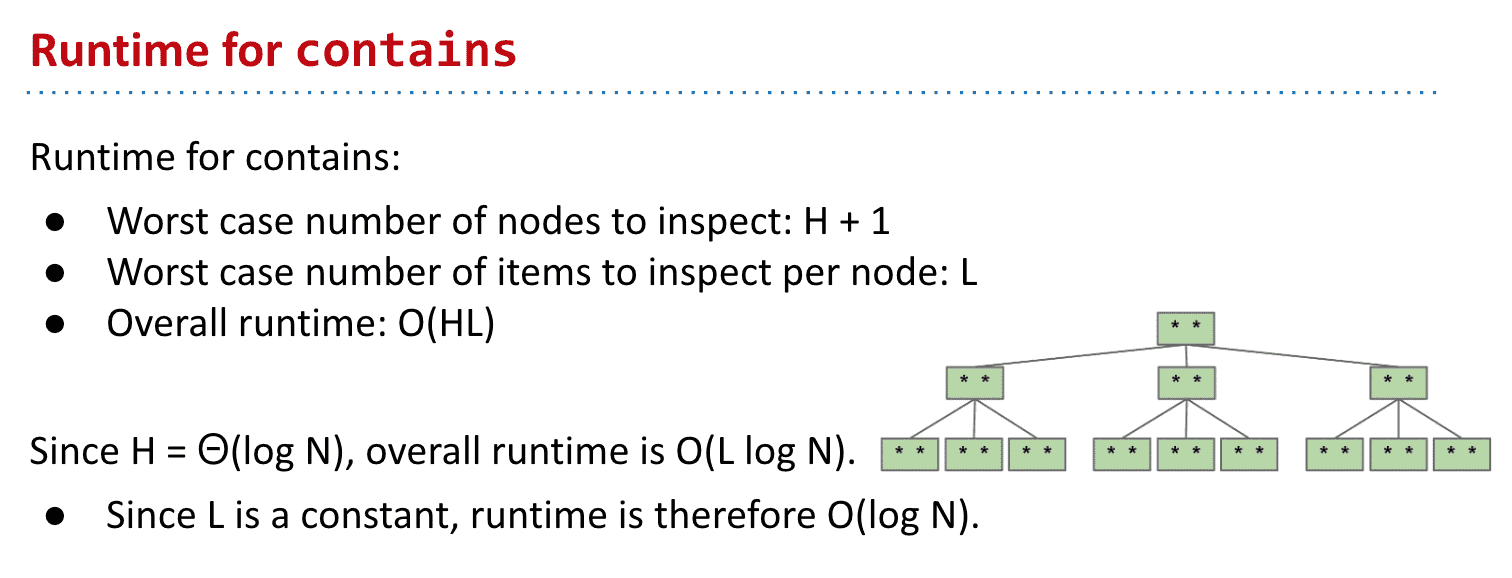
运行时间
如果要删除B树的值,先交换再删除
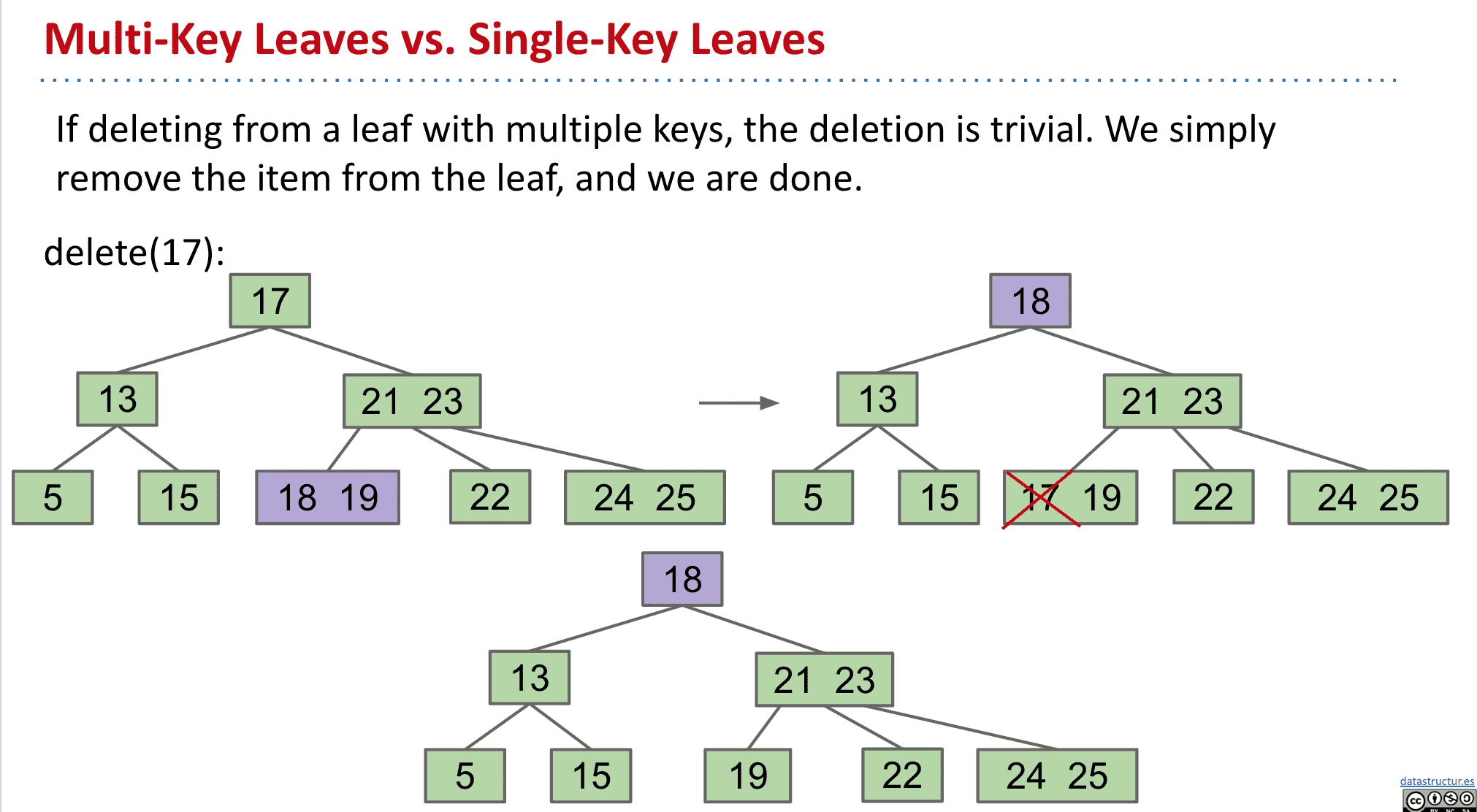
B树或者说2-3树等,实现起来很麻烦,解决这个问题就需要看更快更简单的红黑树了

B树伪代码
2-3树是每一个节点有2个或者3个子节点,2-3-4/2-4树是每一个节点有2、3或者4个子节点的树
B-Tree 的关键思想是在底部过度填充节点以防止增加树的高度,所以B树肯定是平衡的
另外B树的实现很复杂
树旋转 Tree Rotation(BST)
根据添加顺序的不同我们会得到各种BST

可以通过树旋转来调整不同的节点
想象成合并再分开后会更容易操作
记住BST一个节点左边全比它小,又边全比它大的性质
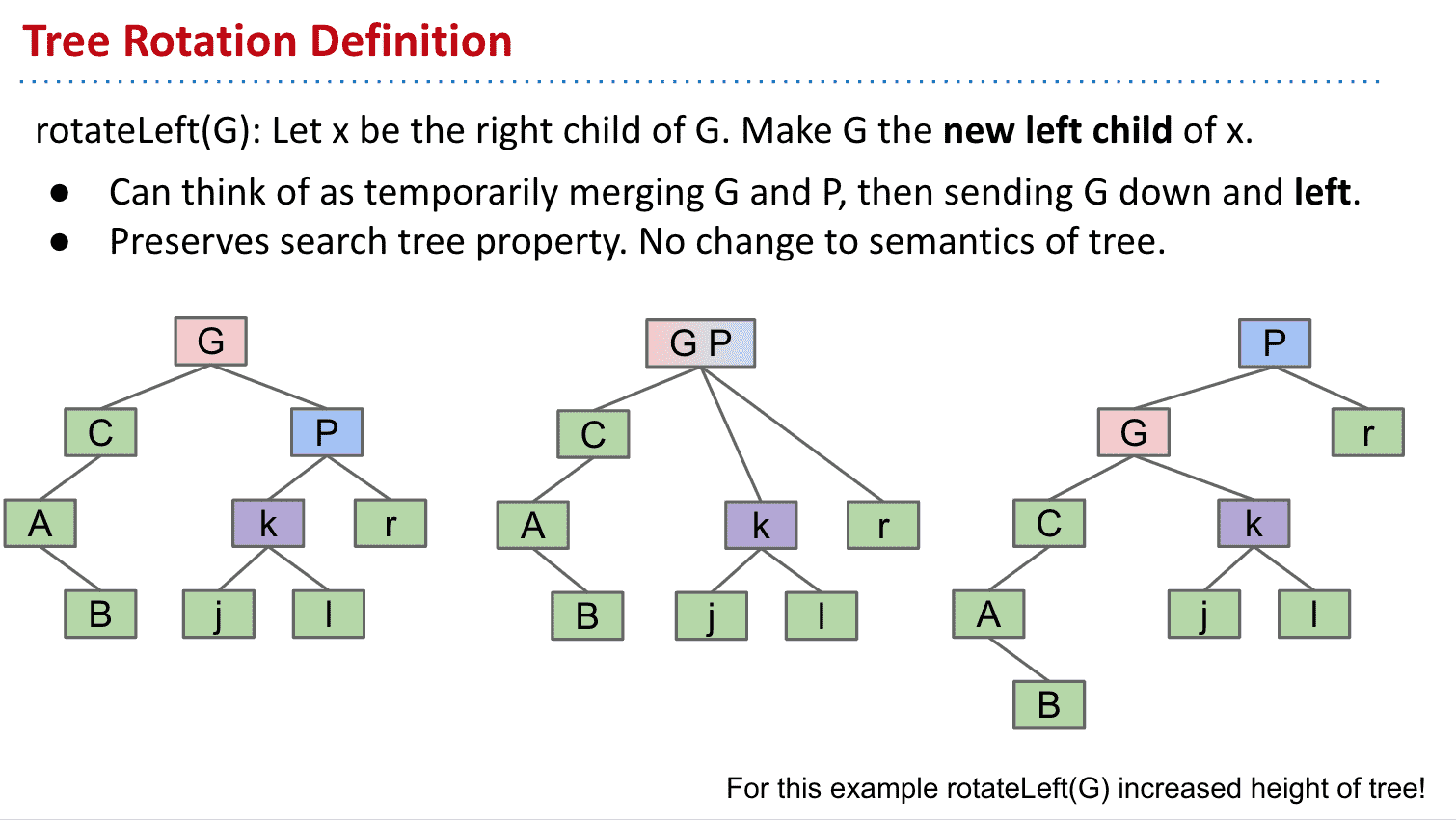
以旋转G到左边为例
树旋转可以让树高度更短或者更长,也有助于维护BST的性质(BST可能会不平衡,所以可以利用树旋转来维护,而B树是自平衡的就不需要树旋转来维护)
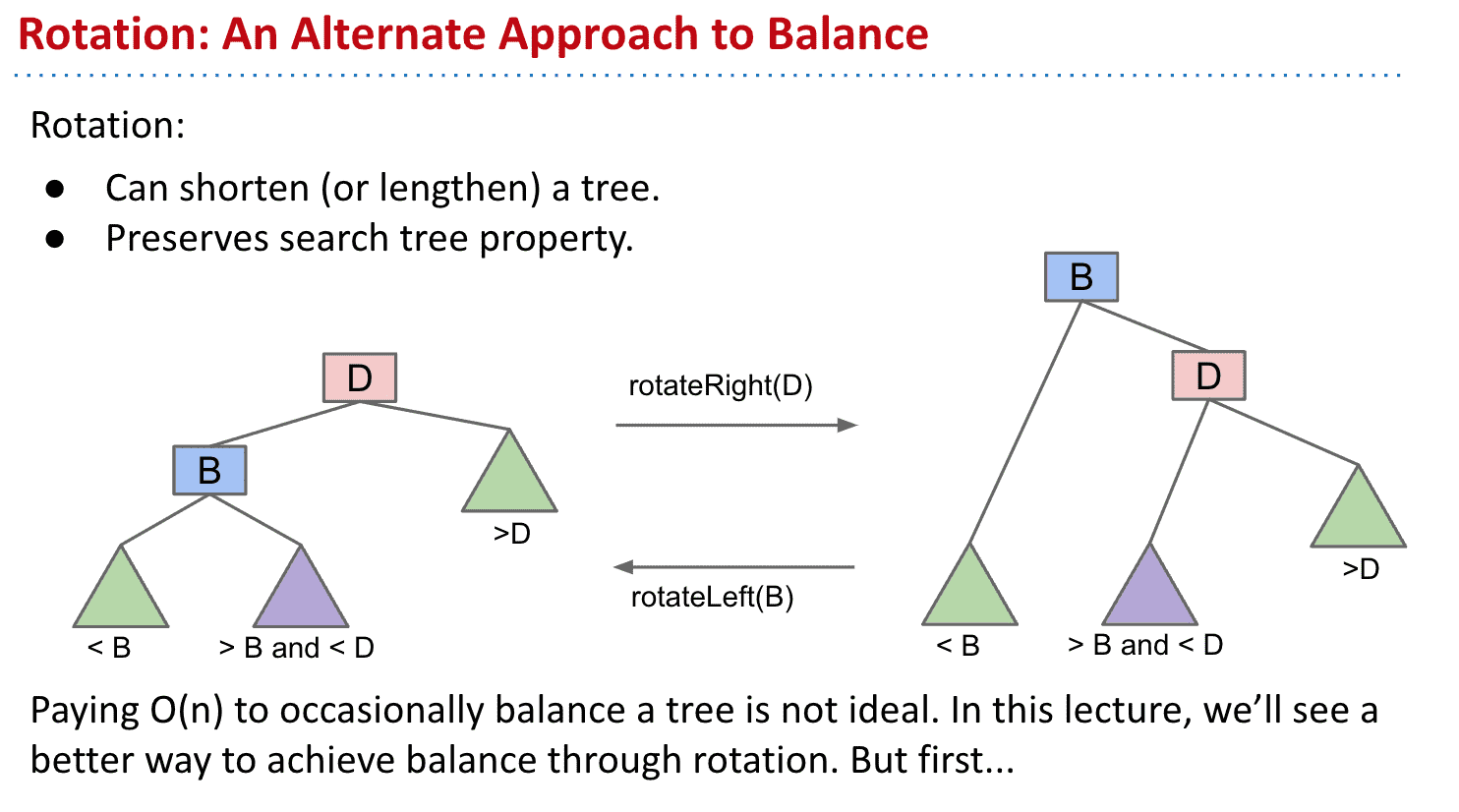
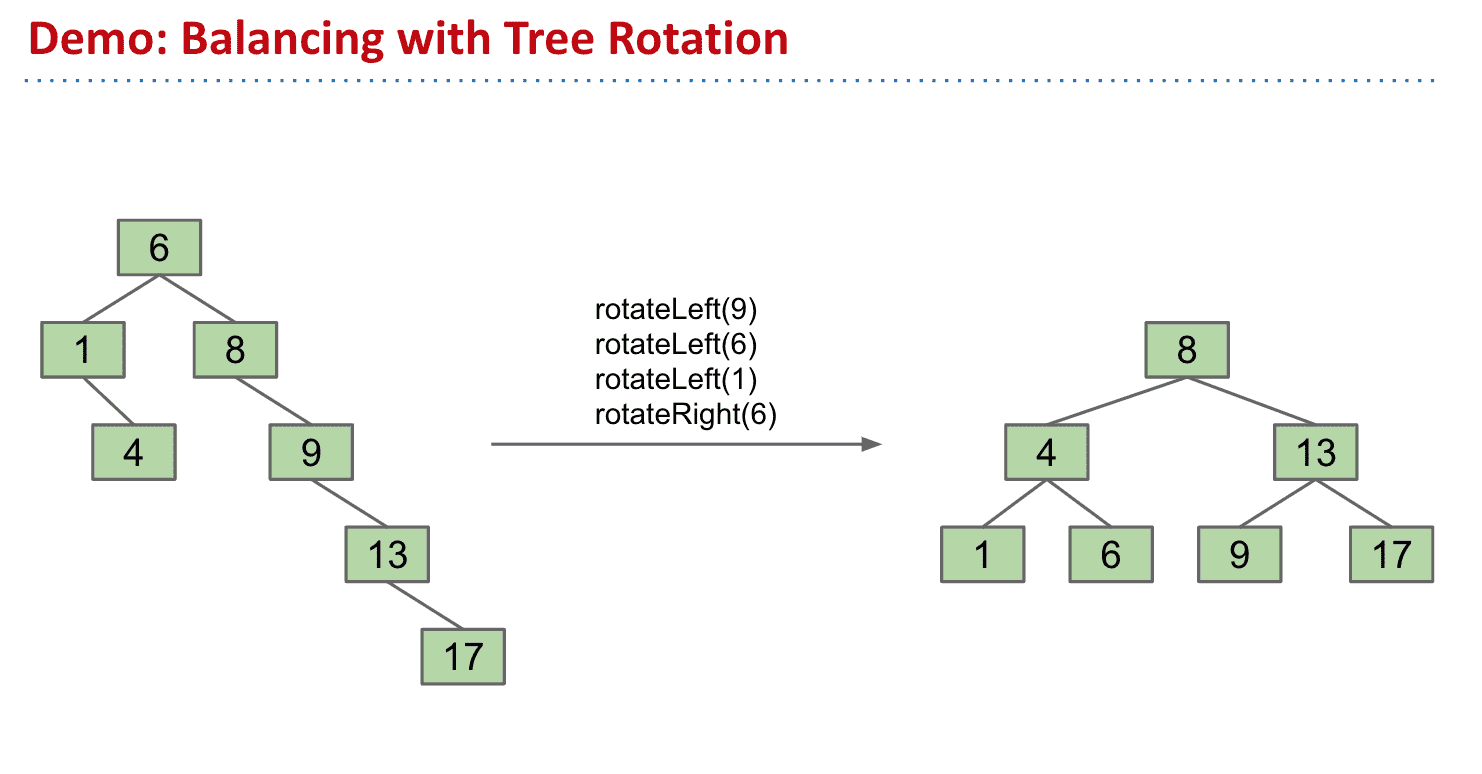
依靠树旋转维护BST
描述一棵树的术语:
**root:**树中最上层的节点,也是唯一一个其父节点为Null的节点
**leaf:**没有子节点的节点称为leaf node。
**external node:**没有子节点的node(和leaf同意)
**internal node:**至少有一個child的node
这个称为4 node,因间隙可以放4个子节点
红黑树 Red Black Trees
建立一个在结构上与2-3树相同的BST
2-3是自动平衡的,所以我们用它来建立一个BST解决BST会有不平衡的问题
2个子节点的2-3树就和BST结构一样
但3个子节点的2-3树呢,怎么样才能变成BST的结构
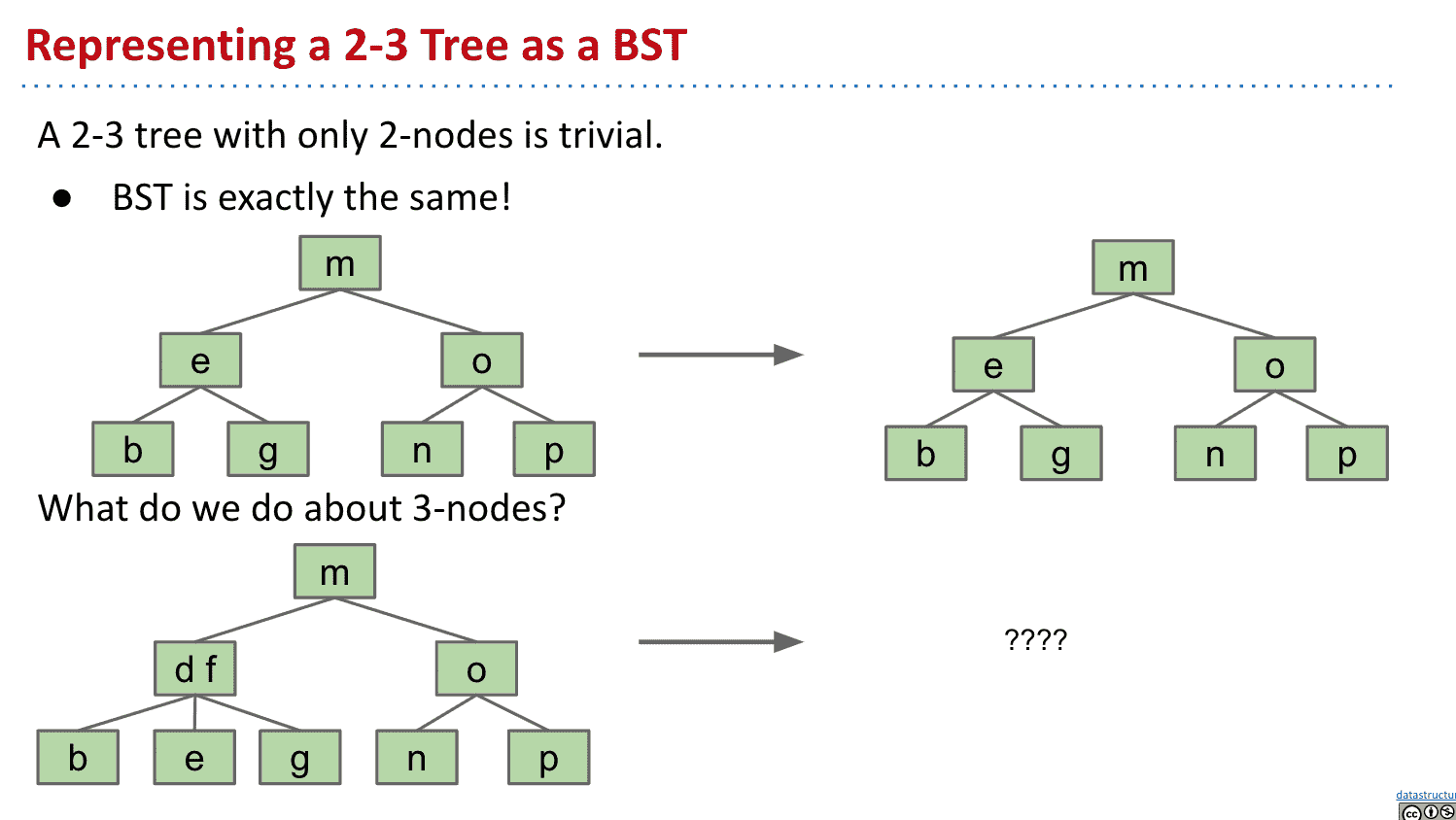
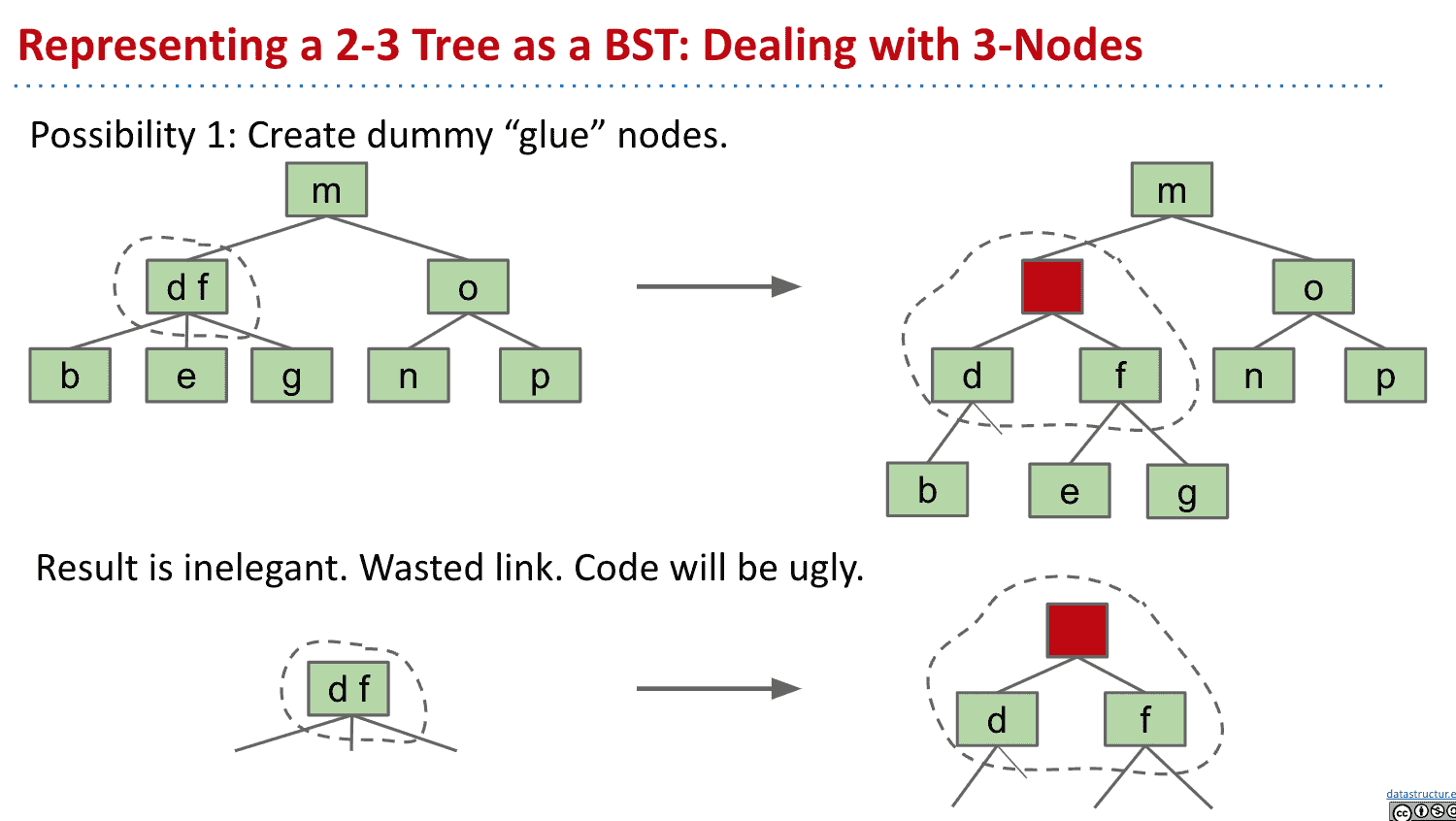
可以建立像哨兵节点(sentinel node)那样不存储值的节点,但是结构会很难看并且丑(但是是可以实现的方法之一)因此选择其他方式实现
使用放在左边(约定俗成)的红色的连接线来表示有两个item的节点
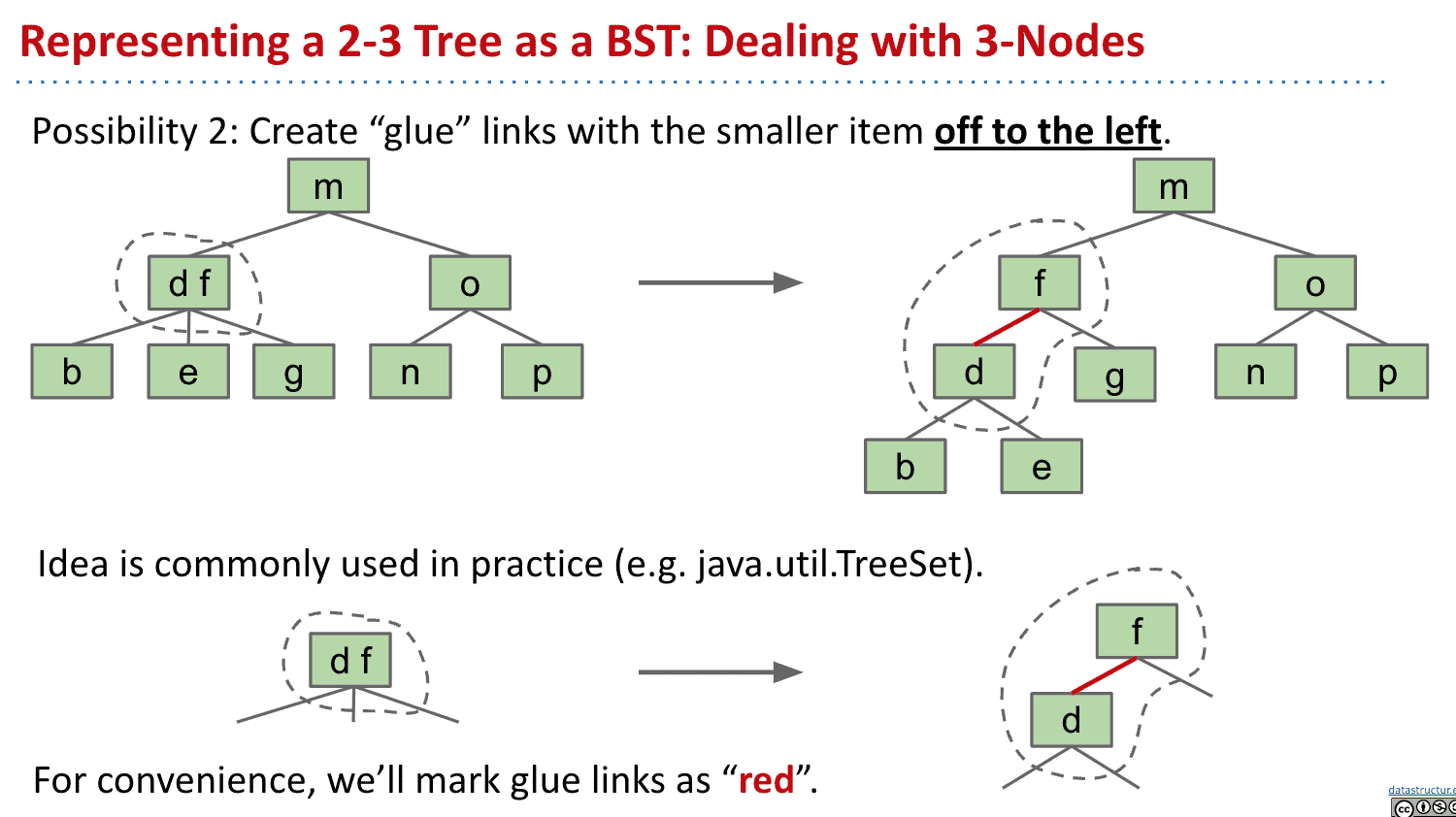
Java中也是这样处理的
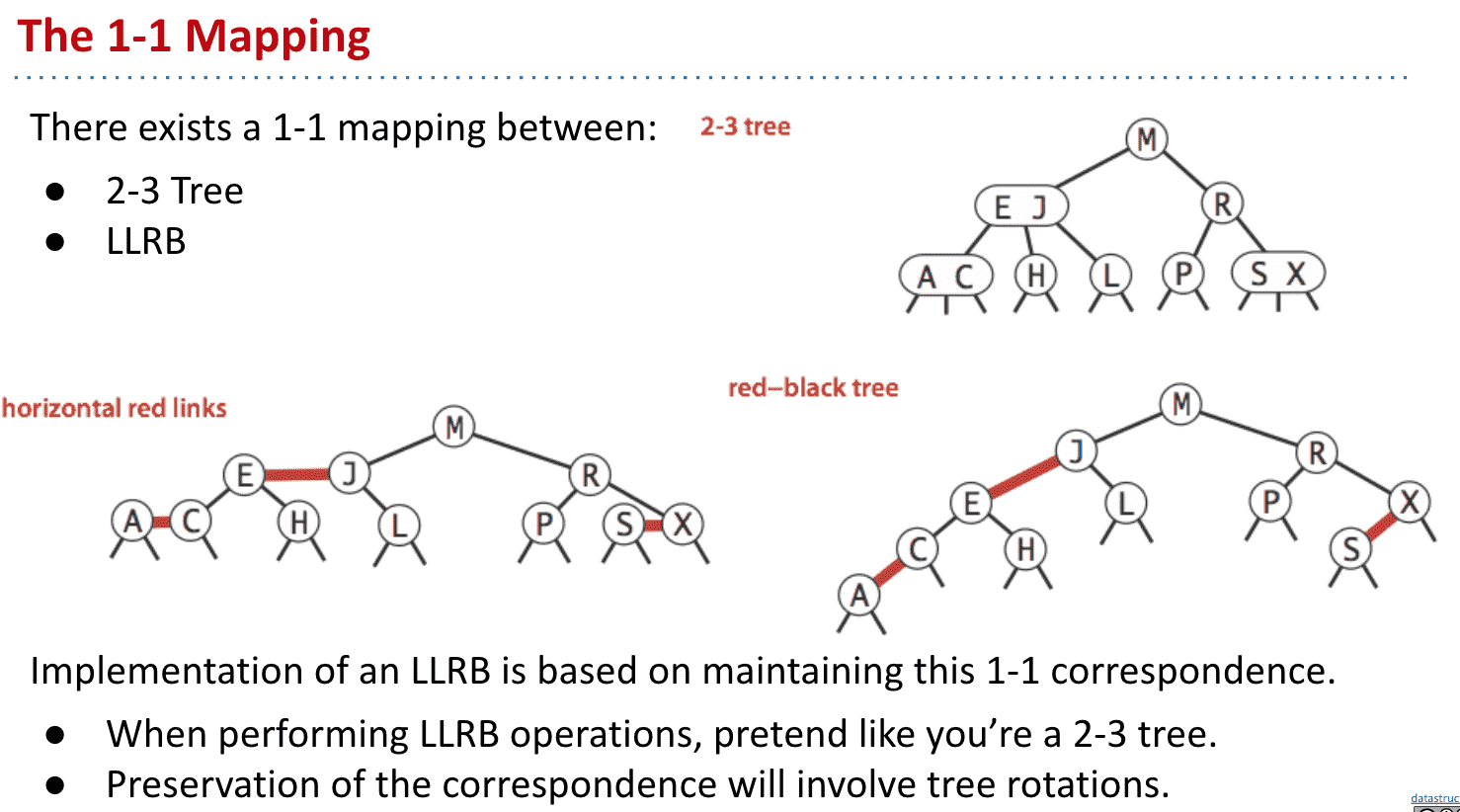
左倾红黑树 LLRB
这样我们就得到了左倾红黑树Left-Leaning Red Black Binary Search Tree (LLRB)
本质上就是一种2-3树表现得像BST,所以每个LLRB都有对应的2-3树
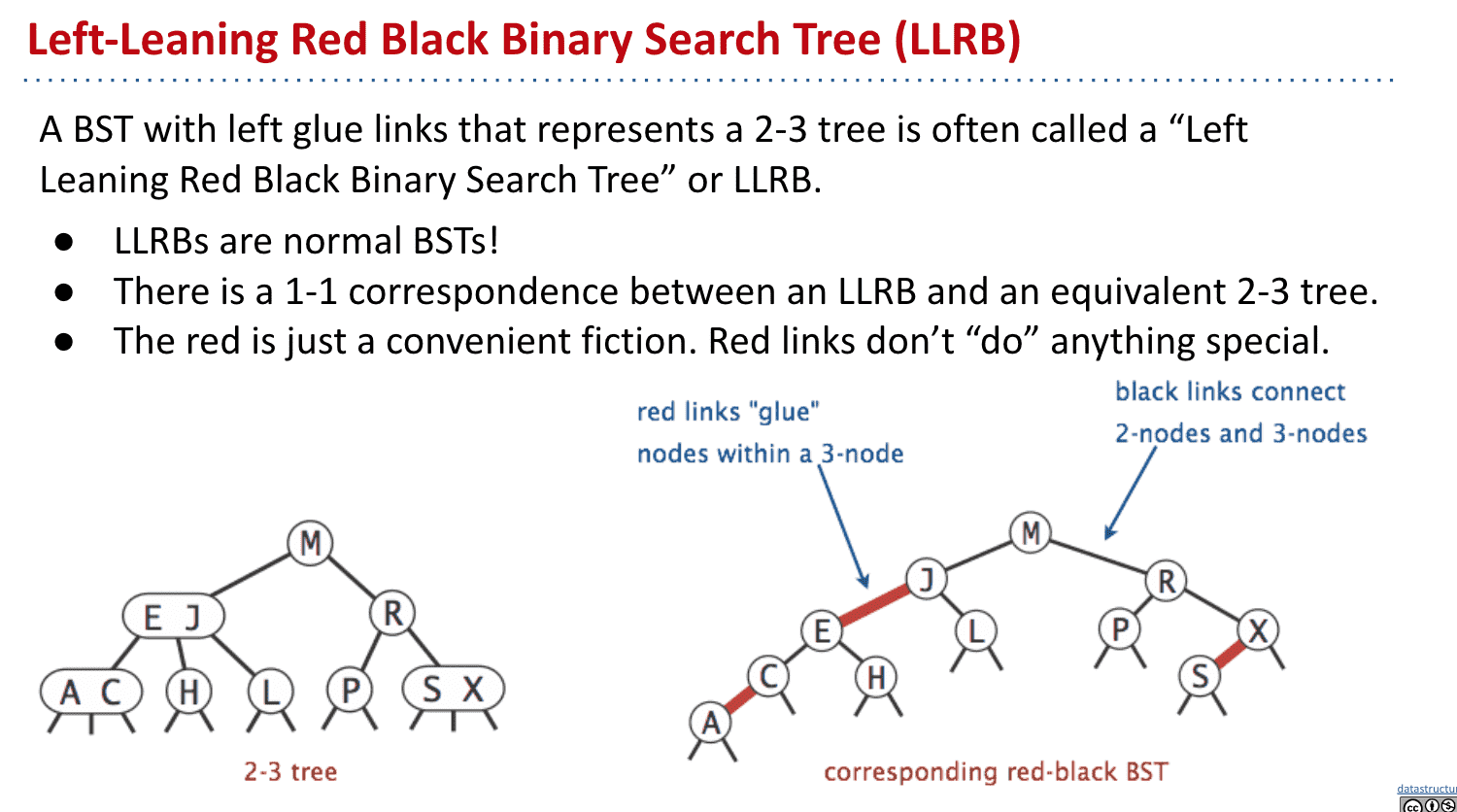
红色link只是种表达方式,并没有特别的作用
LLRB的性质
由于它本质上是2-3树所以:
不会出现一个节点拥有两个红link(这样就会变成一个节点超过2个item了)
leaf拥有的黑link相等(因为2-3树是自平衡的)比如例子第二个leaf“C”到根两根黑线,而X只有一根,说明他们不平衡
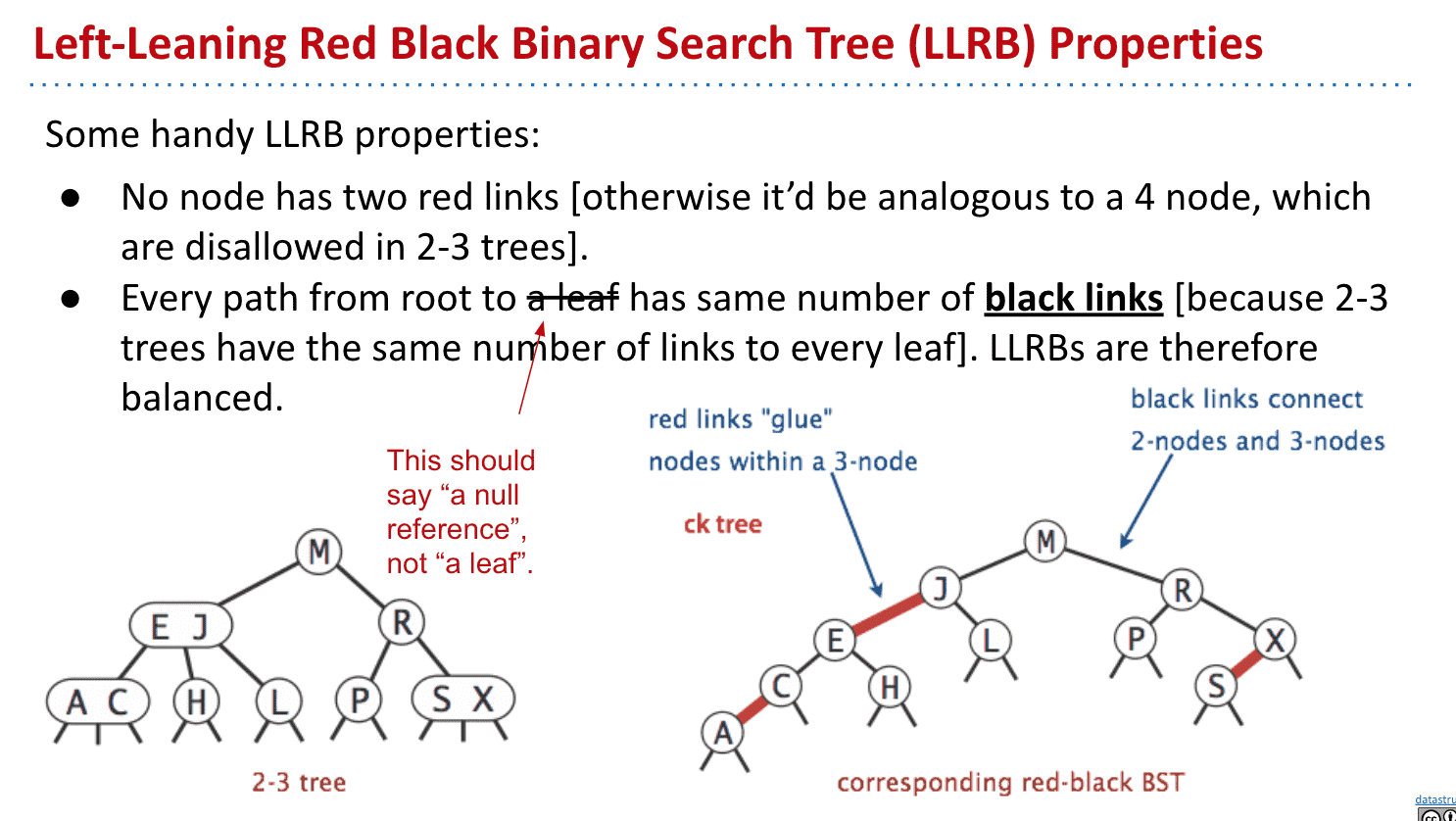
LLRB的性质
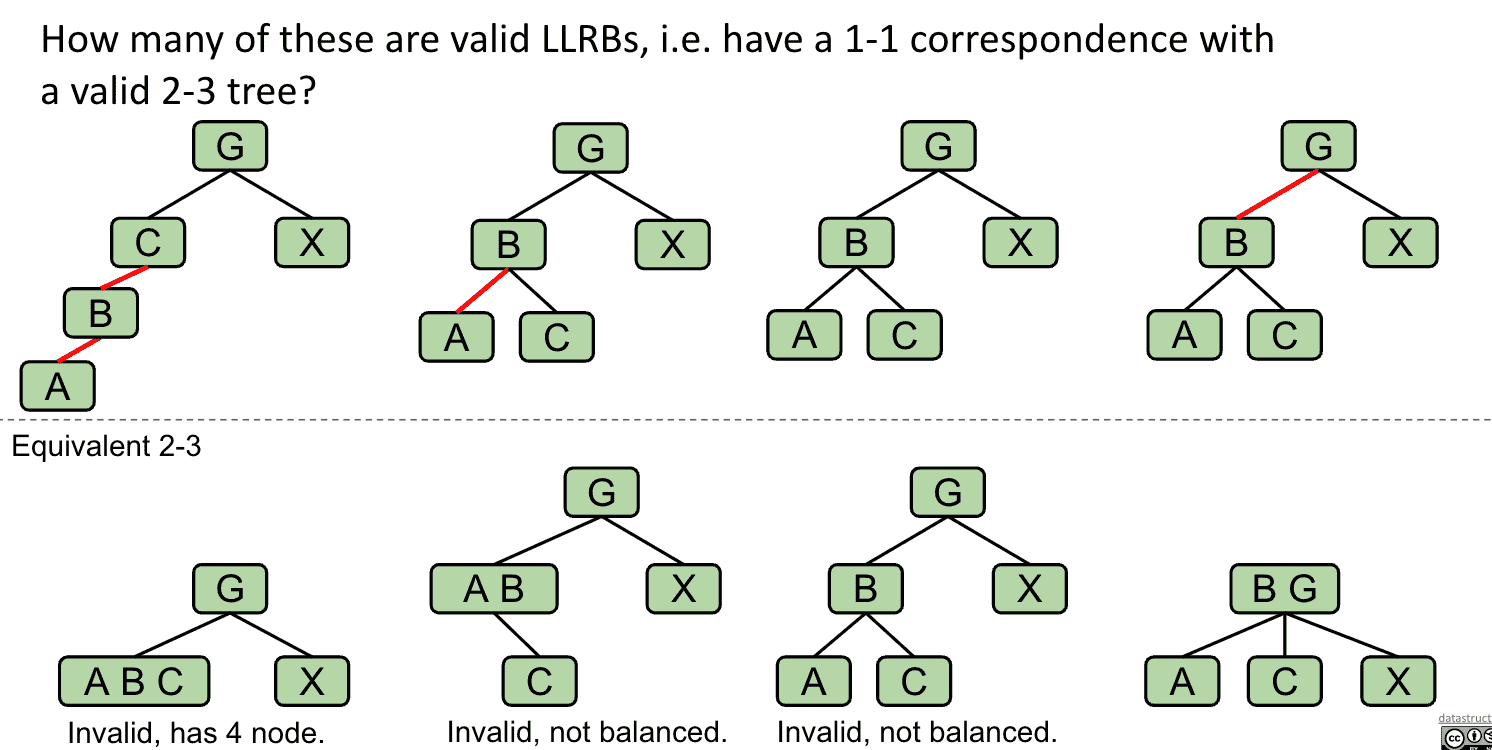
错误的LLRB例子
1.B有2个红线 2、3.黑线不平衡 4.正确的结构
LLRB的Height
最大高度就是2H+1
原本的高H(黑link)
然后每个节点都可能是粉红节点(可以看作一个红link),节点数比H多1
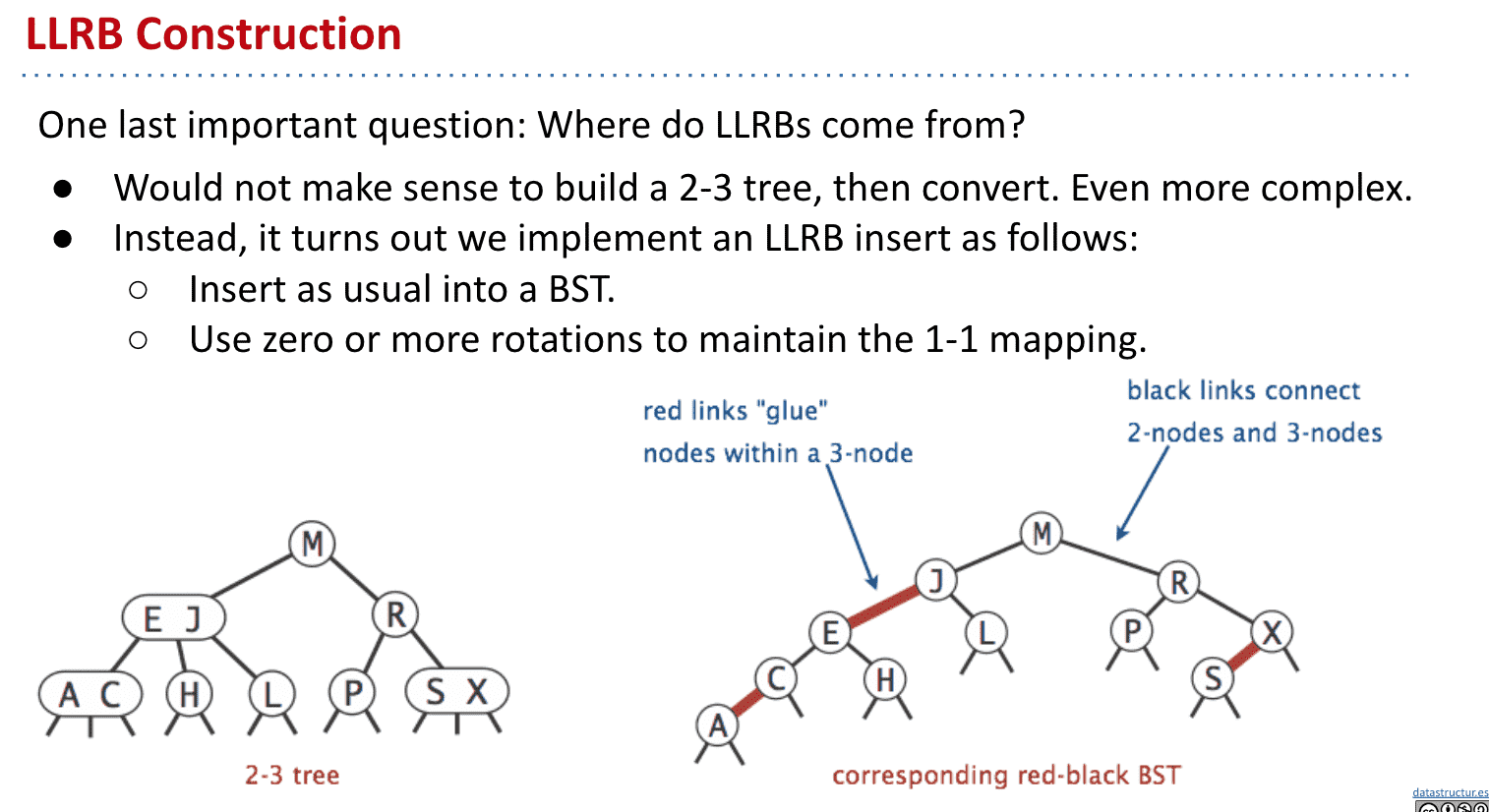
LLRB插入规则
通过Rotations维护红黑树与2-3树一对一的关系
进行修改操作时可以认为就是在修改2-3树
-
当插入新数值时,使用红线左连接
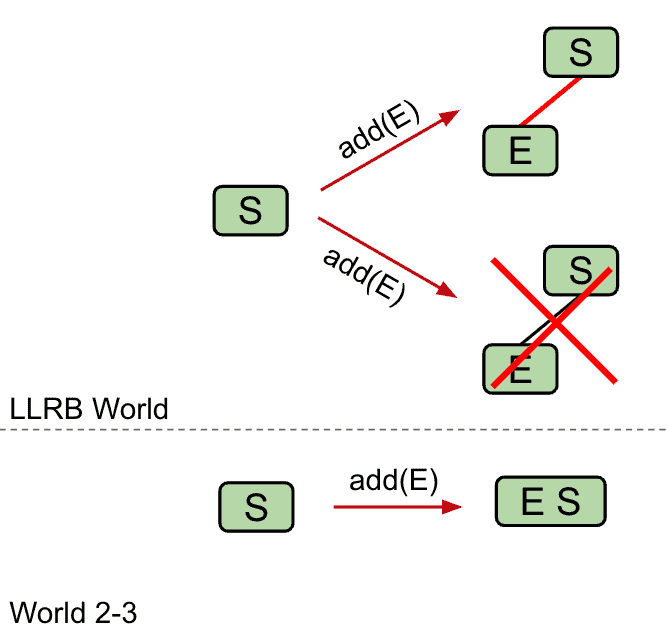
-
如果有右倾的3 node(2个item)就要对合适的node “Rotate left”
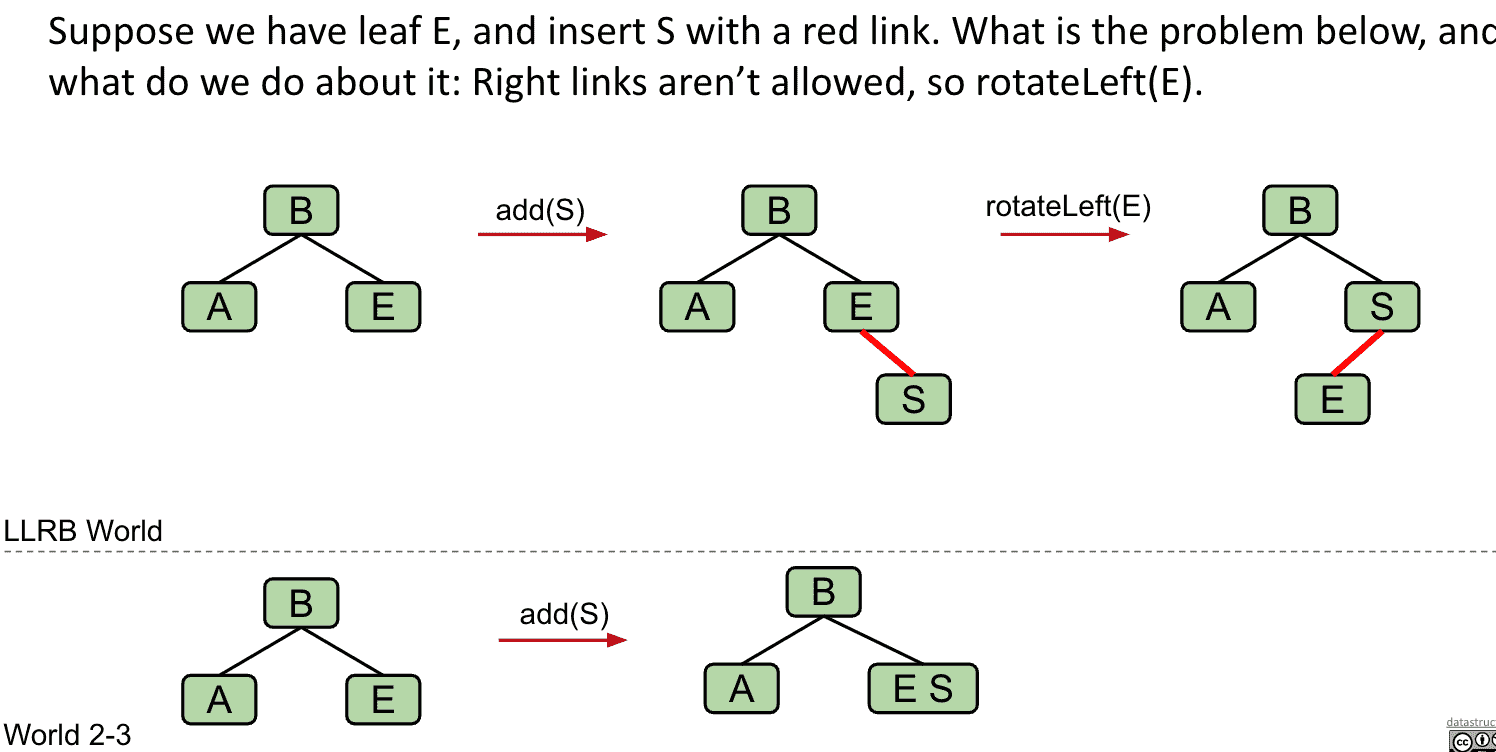
添加S后由于它比E大放在了右边,所以需要把E向左旋转
S是右倾红线连接所以旋转B到左边修复成LLRB
-
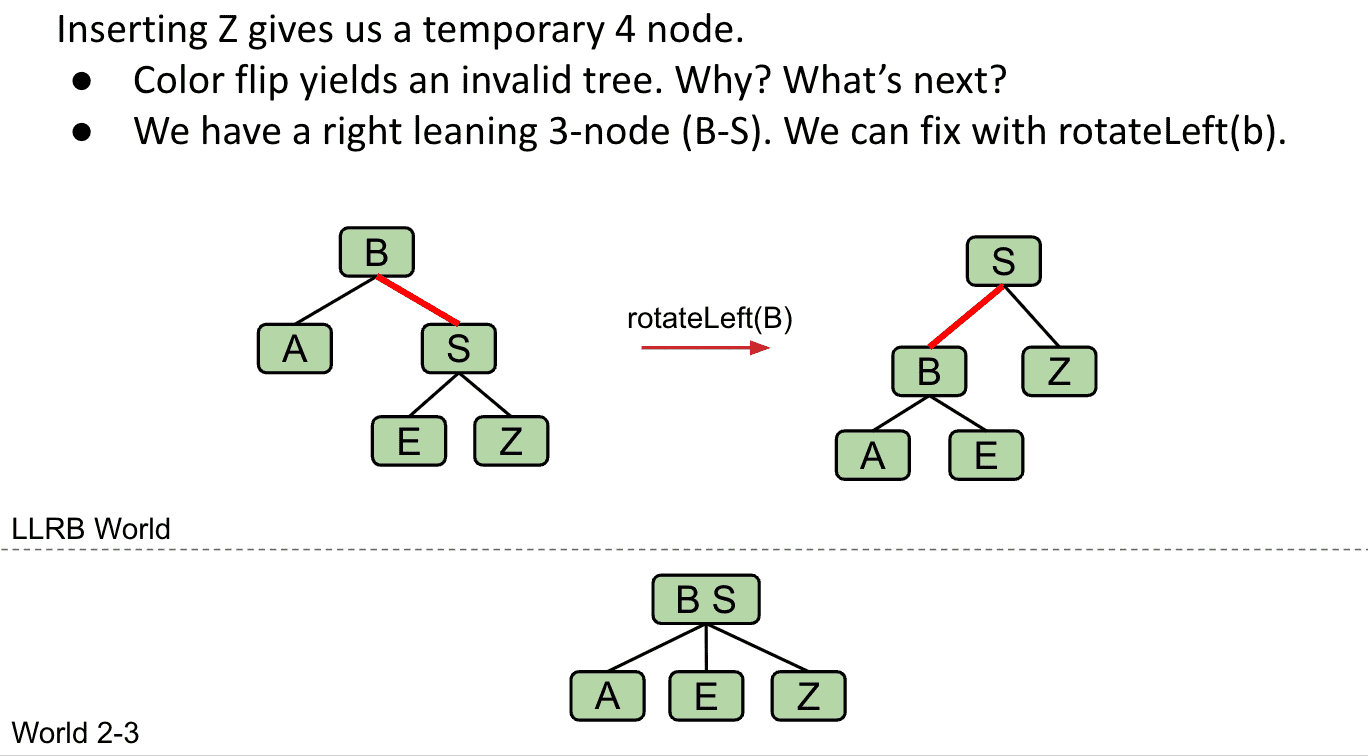
如果有两个连续的左边红线,就会产生4 node 就要对合适的node “Rotate right” (临时 )
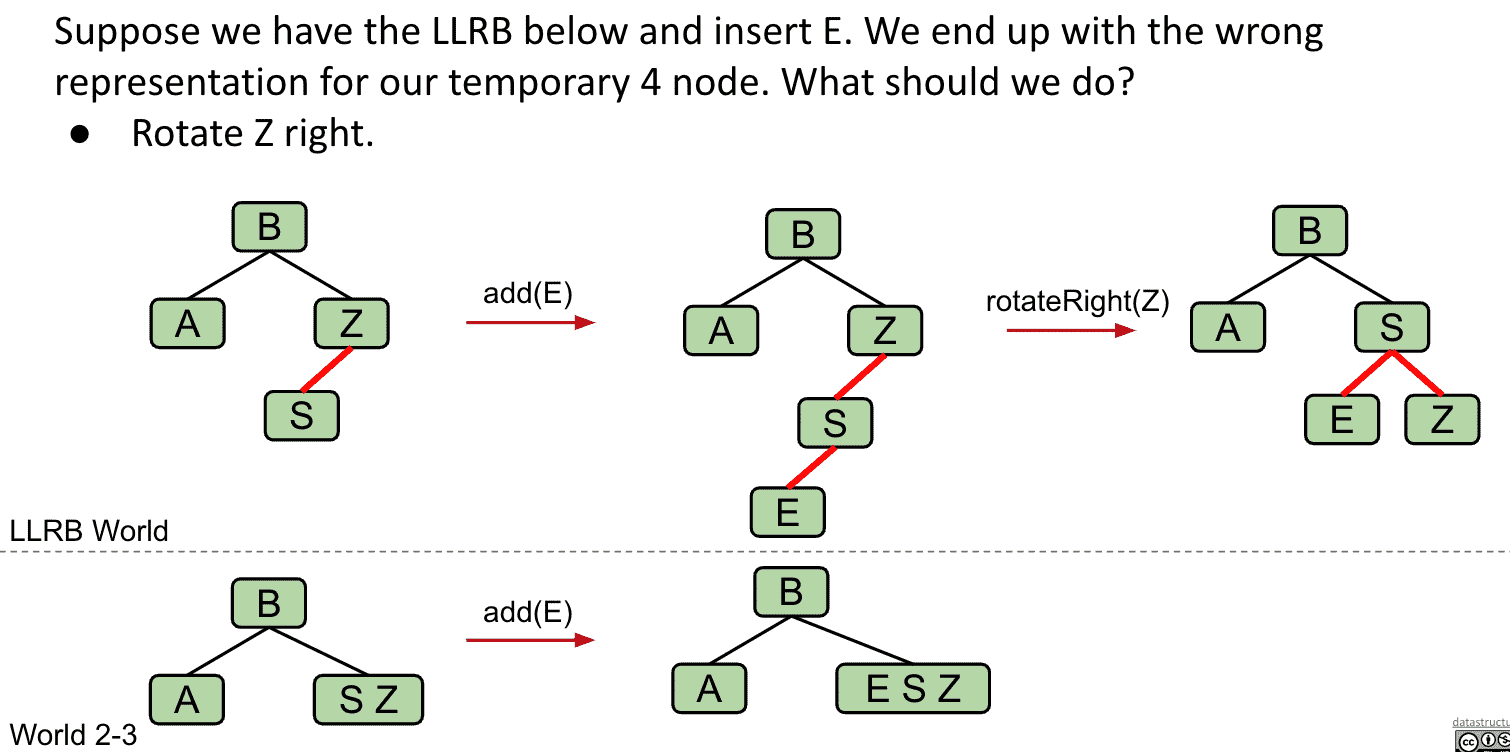
S两个子节点都是红线连接的问题下面解决
-
如果有任何node有两个红线子节点,就产生了临时4 node(3个item),需要对node进行颜色翻转,以模拟分割操作(因为要一对一,结构不会发生变化)
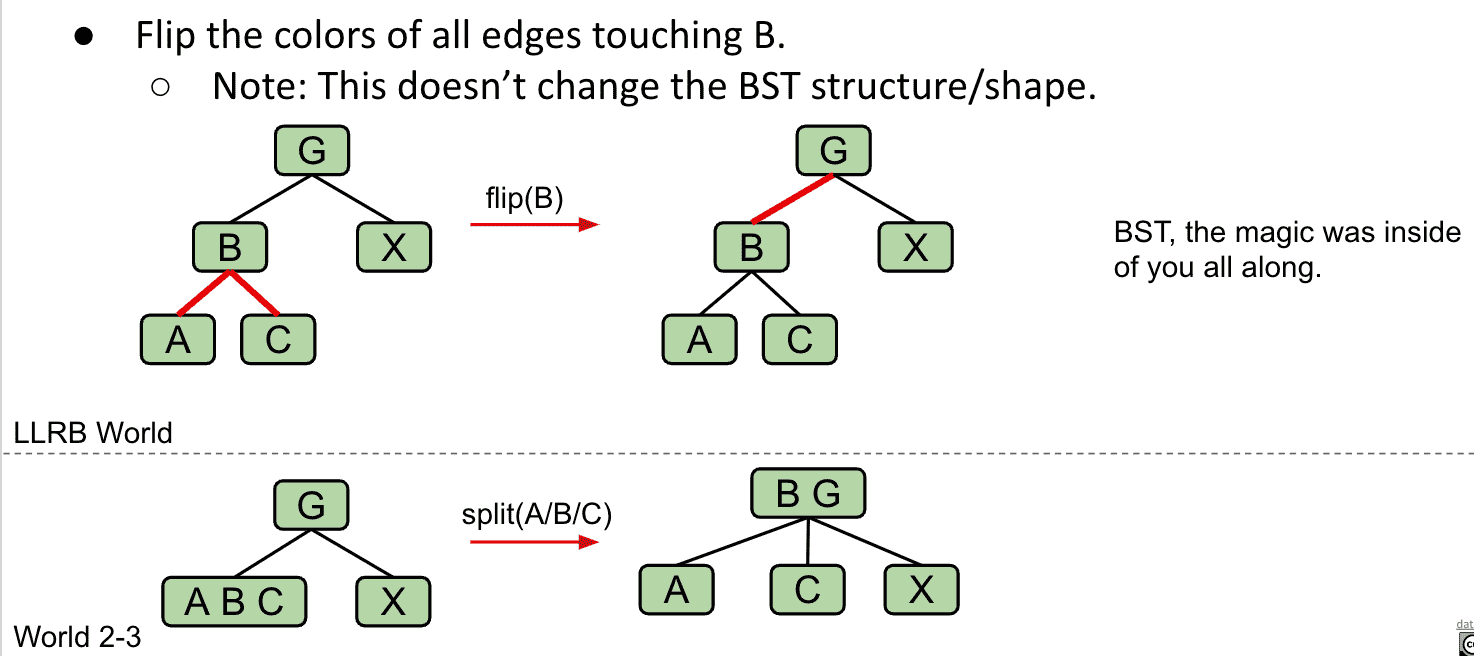
B有两个红线连接子节点,于是翻转B相关的线颜色,2-3树结构没有变化,但相当于把B与G合并了

由于本质是2-3树高度和查找都一样,只是有旋转操作会花费更多时间

LLRB实现需要考虑的规则
LLRB总结
- BST很简单但是不会自平衡
- 2-3树(B树)会自平衡但是难实现
- LLRB(红黑树)实现简单(删除实现困难),只需要在BST的基础上加上各种旋转的规则(表现像2-3树) 用BST的结构实现了2-3树的功能解决了2-3树难以实现的问题
和2-3树有一对一的关系
Java使用的红黑树不是左倾的,并且是2-3-4树(没有一对一关系),允许两边都有红线,速度更快
似乎我只学了2-3树并且左倾情况下的特殊的红黑树,以后还得继续深入啊~
散列表Hash table (哈希表)
Data Indexed Arrays(只是为了课程设计的结构)
用index作为data,存储data是否存在(true/false)
我们已经知道了Set和Map的几种实现方式
但我们并不一定需要对他们的item进行比较(而且有些item不可以比较)能不能避免比较呢
性能虽然很棒了,但能不能更进一步呢
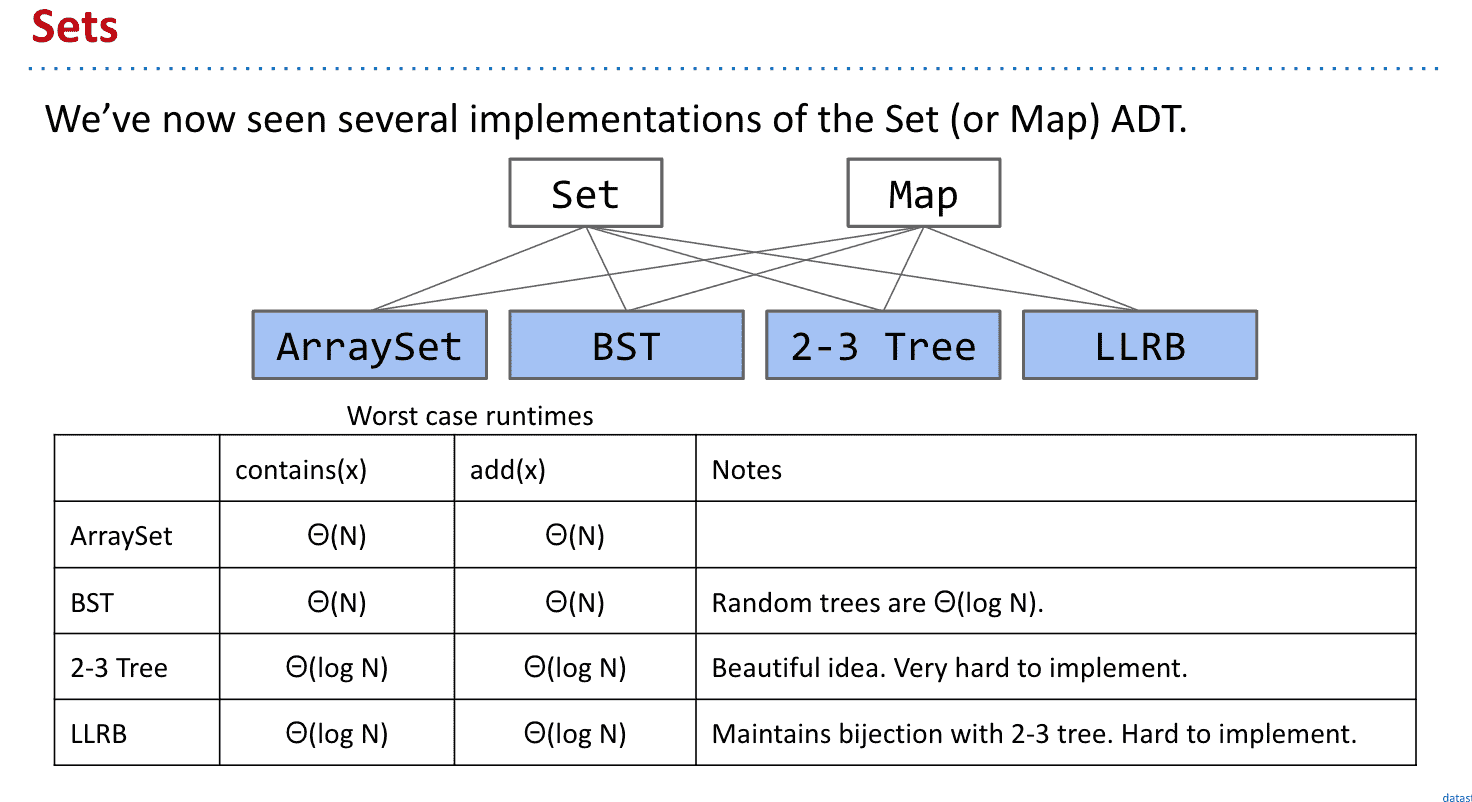
所以我们可以设计一个index就是data本身,然后存储的东西就是有没有这个data的数组
这样运行效率就很快

用index作为data,存储true和false表示有没有这个data

实现代码
缺点是会浪费大量内存,因为我们需要给把所有数字都设为false
并且我们只能存整数,下面的结构将会扩展到存储英文

DataIndexedEnglishWordSet
我们可以长度为26的数组,代表a~z
这样就可以把“cat”存入3了(c开头)
这样有两个问题
- 很容易就重复了
想找”huhu“时可能为“hub“存过了所以显示”huhu“也存在 - 无法存储数字开头的东西

首先为了防止冲突可以使用如图的方法为每个单词生成不会重复唯一的字符
但是这个方法不支持大写字母也不支持数字


就像数字不会重复一样,27也避免了字母组成重复

只要base≥ 26就不用担心重复问题
想象成给每个字母划了一块内存然后一个单词由多个字母组成
DataIndexedStringSet
ASCII是基于拉丁字母的一套电脑编码系统。它主要用于显示现代英语
用126个代表的ASCII为base就可以解决大小写和数字不能存储的问题

ASCII 33以前的是换位符之类不能打印的字符

使用ASCII存储例子
不能存储像中文等非英文词,我们使用Unicode的话就可以支持了
但问题又来了,这样一个简单的词需要的index都会非常巨大
就会造成Integer Overflow
Java的最大整数是:2,147,483,647,超过就会回到-2,147,483,648
比如omens(base:126)= 28,196,917,171最后会变成-1,867,853,901

散列值 Hash Codes
简单来说就是通过一种计算方式把所有东西都计算出一个较小的值,一样的东西得到的散列值是相同
因为值小所以不可避免地会重复
比如(“melt banana” vs. “subterrestrial anticosmetic”)是一样的值,而解决这个问题叫collision handling
Java中所有对象都有散列值(.hashCode()
),如果对象改变散列值也会改变

Hash Tables:Handling Collisions
为了解决不同对象相同的散列值可能造成的冲突,可以把存储true/false改为存储这个对象
比如创建一个LL放对象然后存储指向LL的地址
有新的对象直接加在LL里就可以了,重复的添加忽略就可以了

改为index存储添加的对象列表
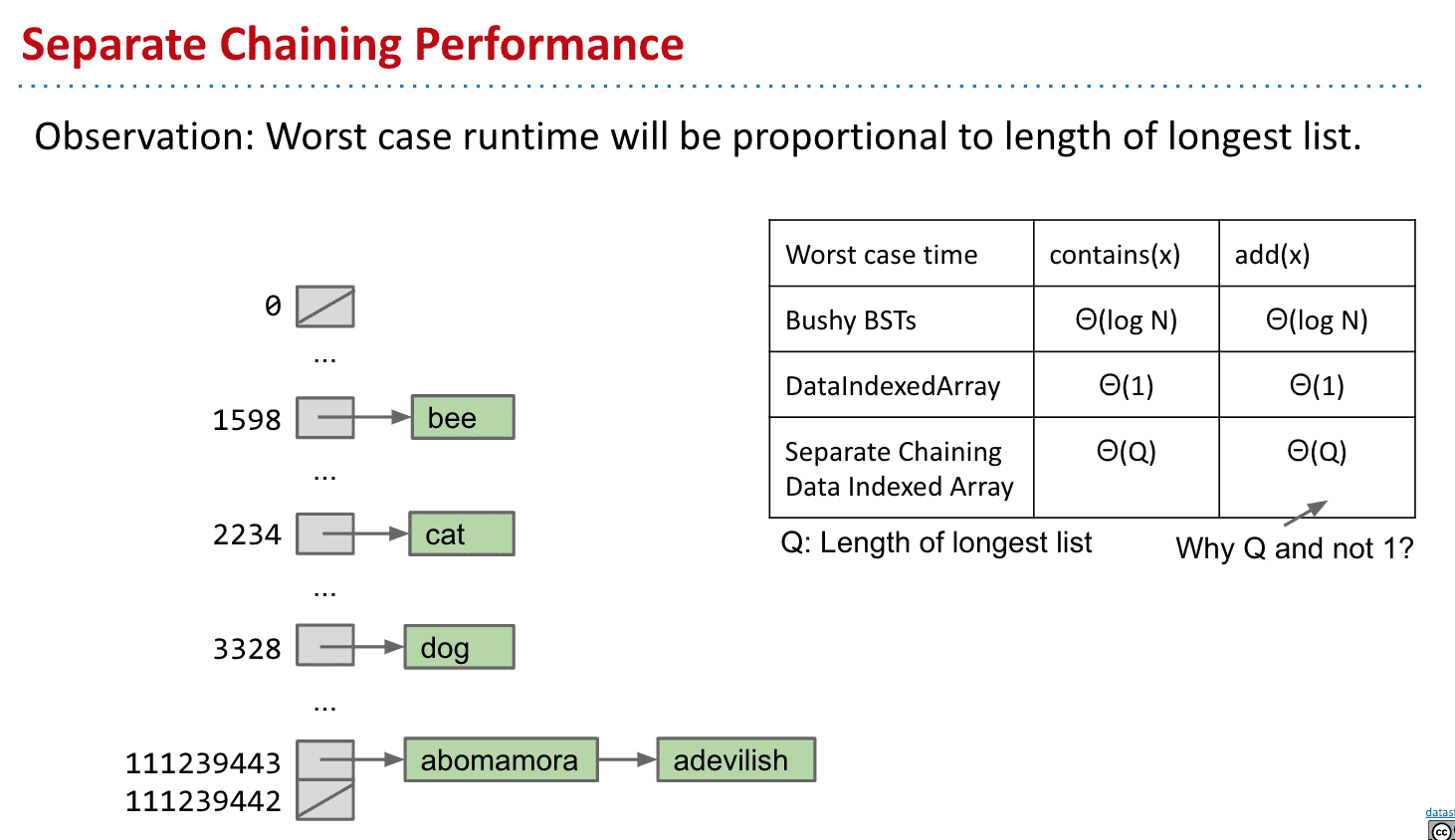
运行速度要取决于对象散列值对应index储存的list长度
建立散列表 Hash Table
节省内存
有大量index并没有被使用,所以我们可以取余 把散列值余数相同的对象放在一起
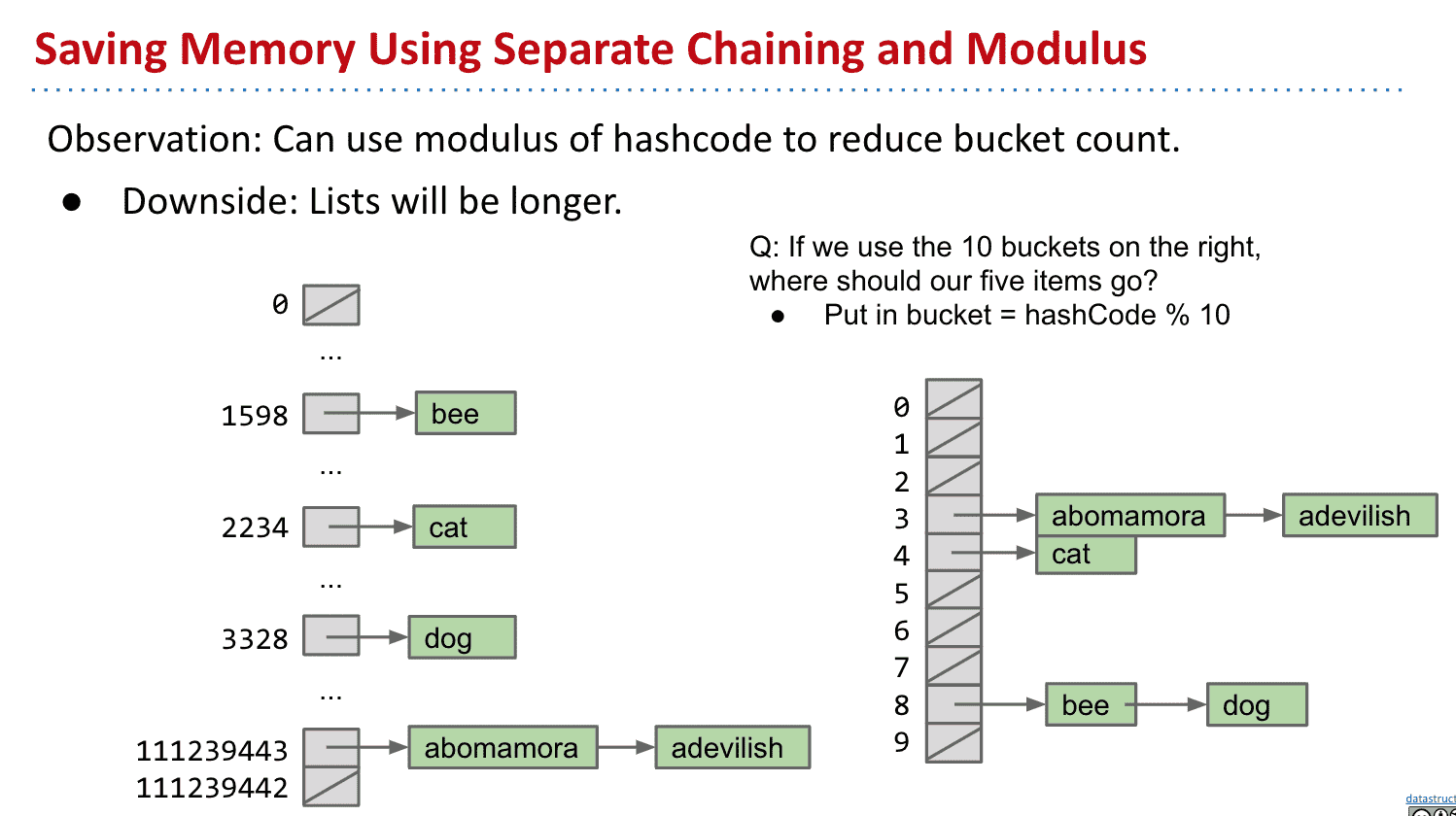
通过这种操作我们就成功建立出了散列表了!
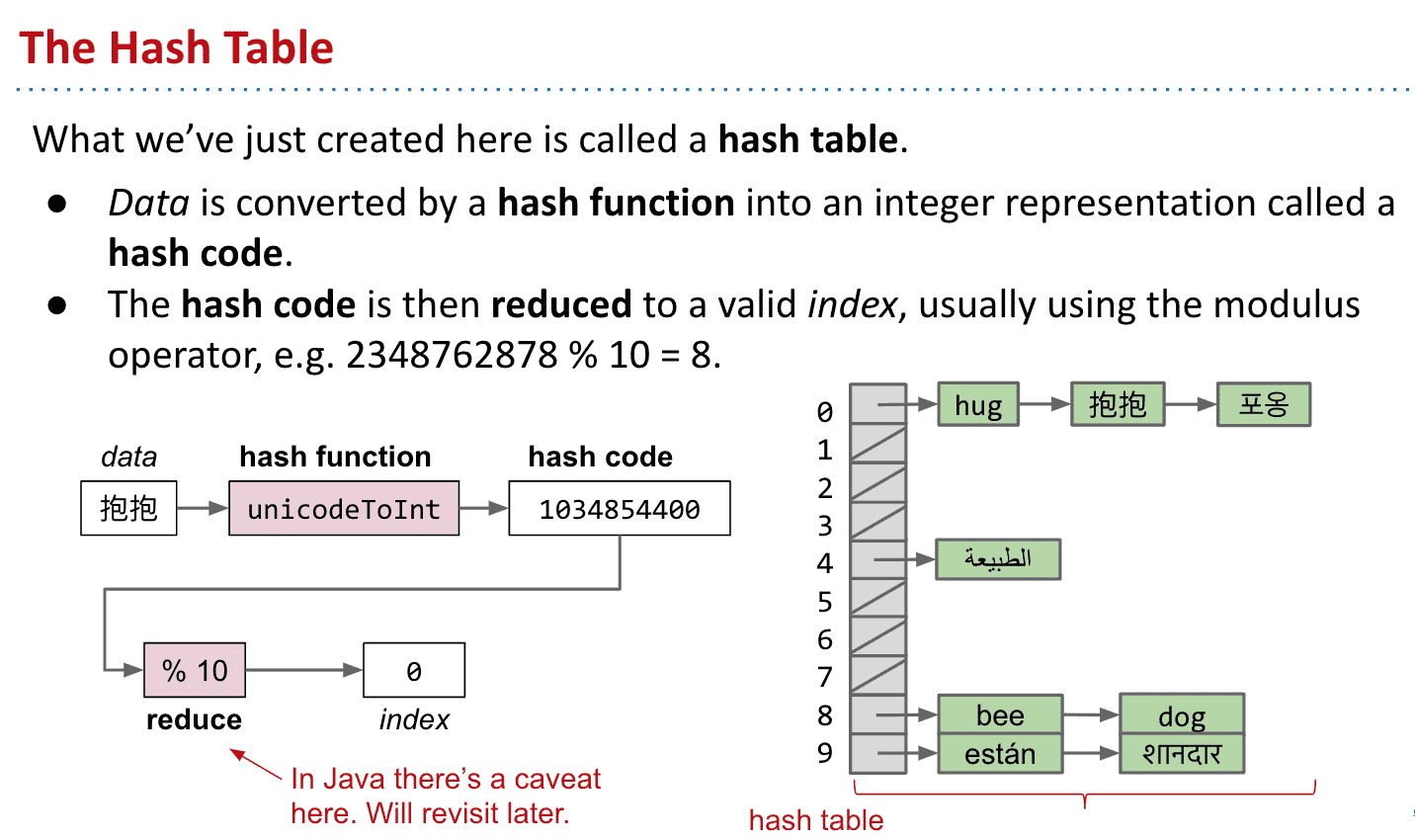
哪怕散列值不同的对象也被存储在一个bucket里
散列表运行时间
虽然节省了空间,但运行时间也增加了,最坏的时间取决于存储的最长列表
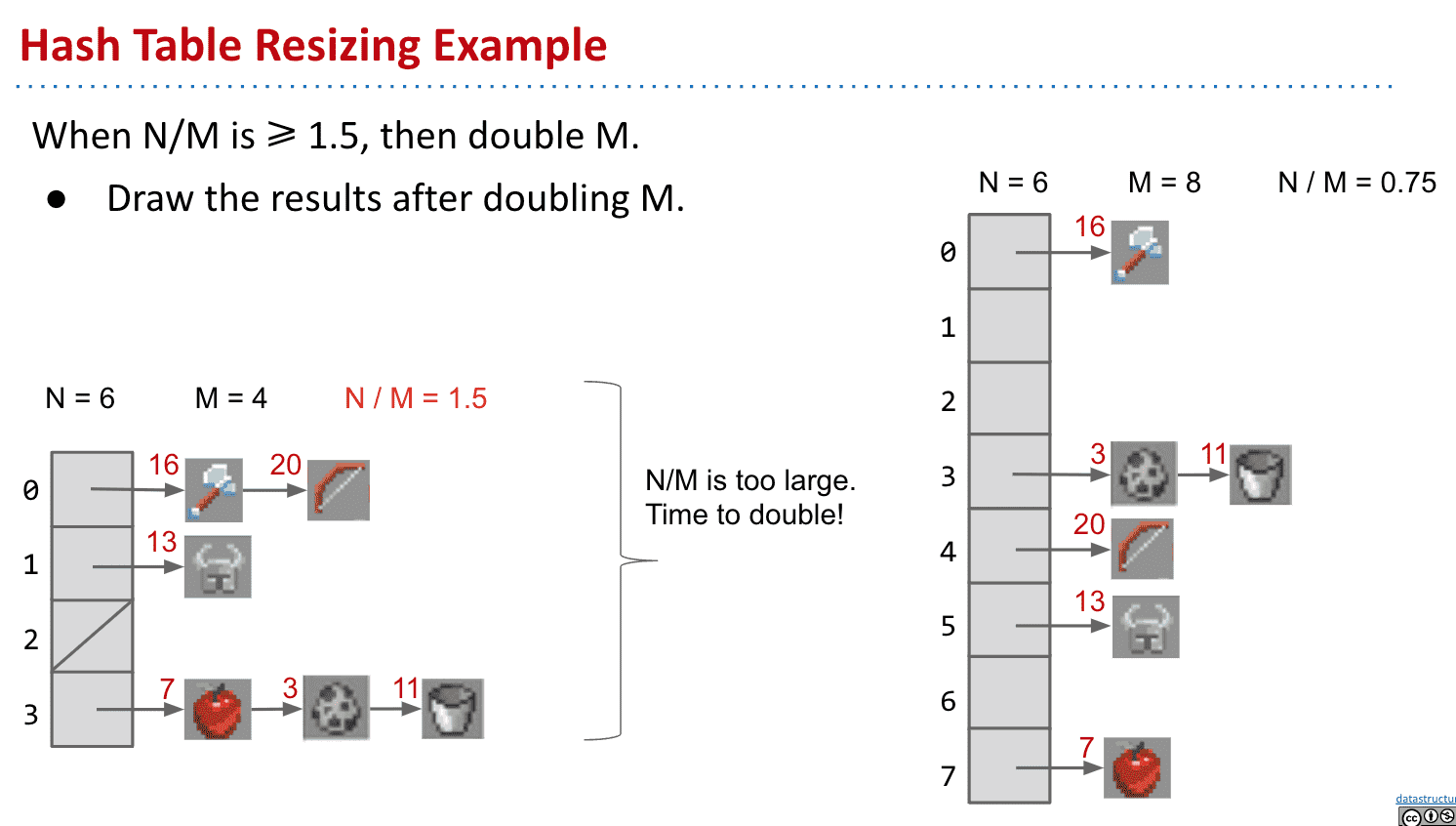
1.5只是随便选的值,
M代表bucket数量, N代表item数量
Java中的散列表 Hash Tables in Java
sets和maps很多都是依靠散列表实现的
因为性能出色,不需要对象可以比较,实现相对简单
像python的dictionaries就是散列表
在Java的实现为java.util.HashMap 和 java.util.HashSet
并且每个Java对象都有.hashCode()的方法可以给出对象的散列值
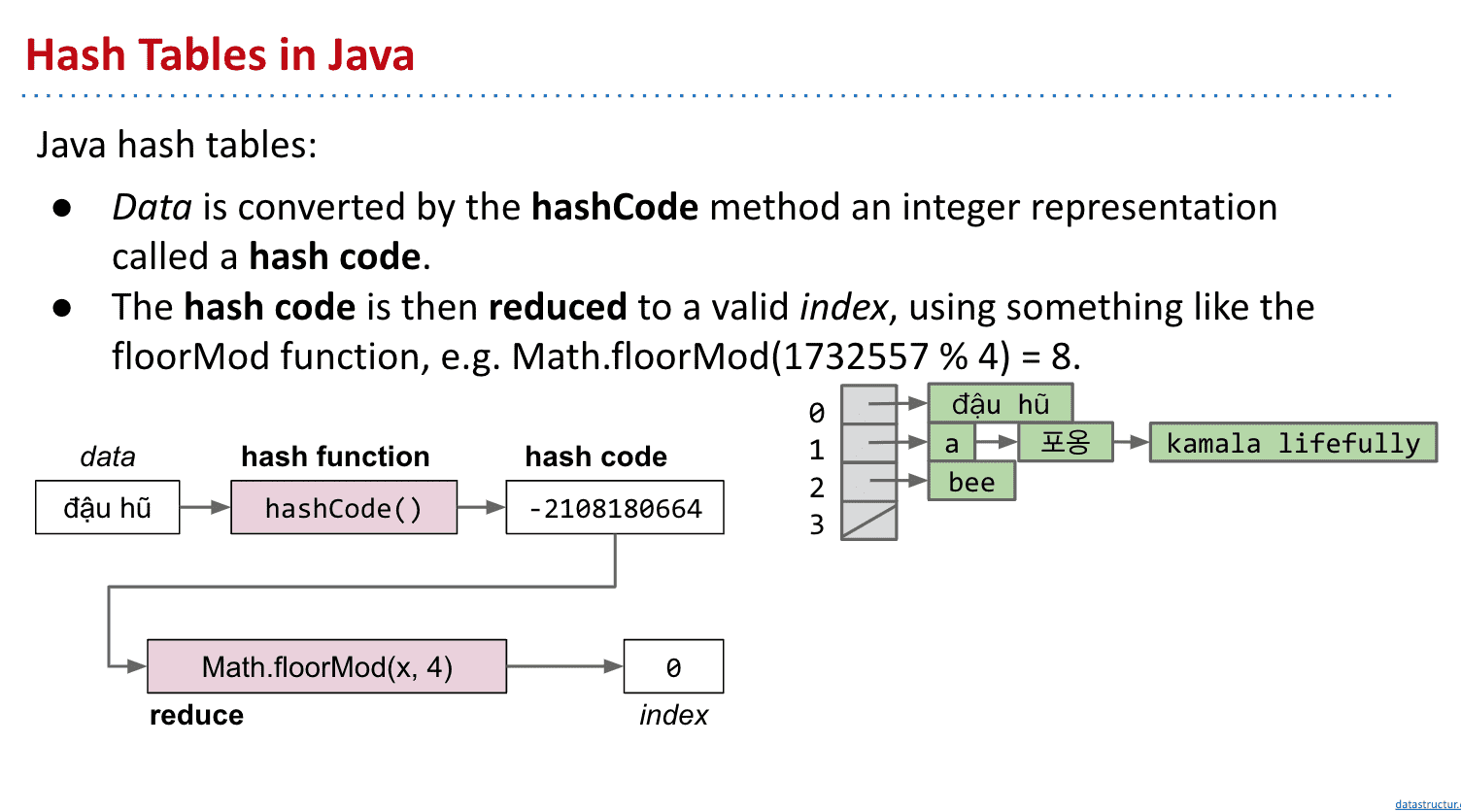
使用HashMaps/HashSets的注意事项
- 不要存储会变化的对象到里面,因为对象变化散列值也会变化
- 不要在不重写hashCode的情况下重写equals(原因如图)
如何实现一个好的HashCodes()方法

好的****.hashCode()****会让item更分散在不同bucket
使用base的计算方式就不错(如上面提到的)
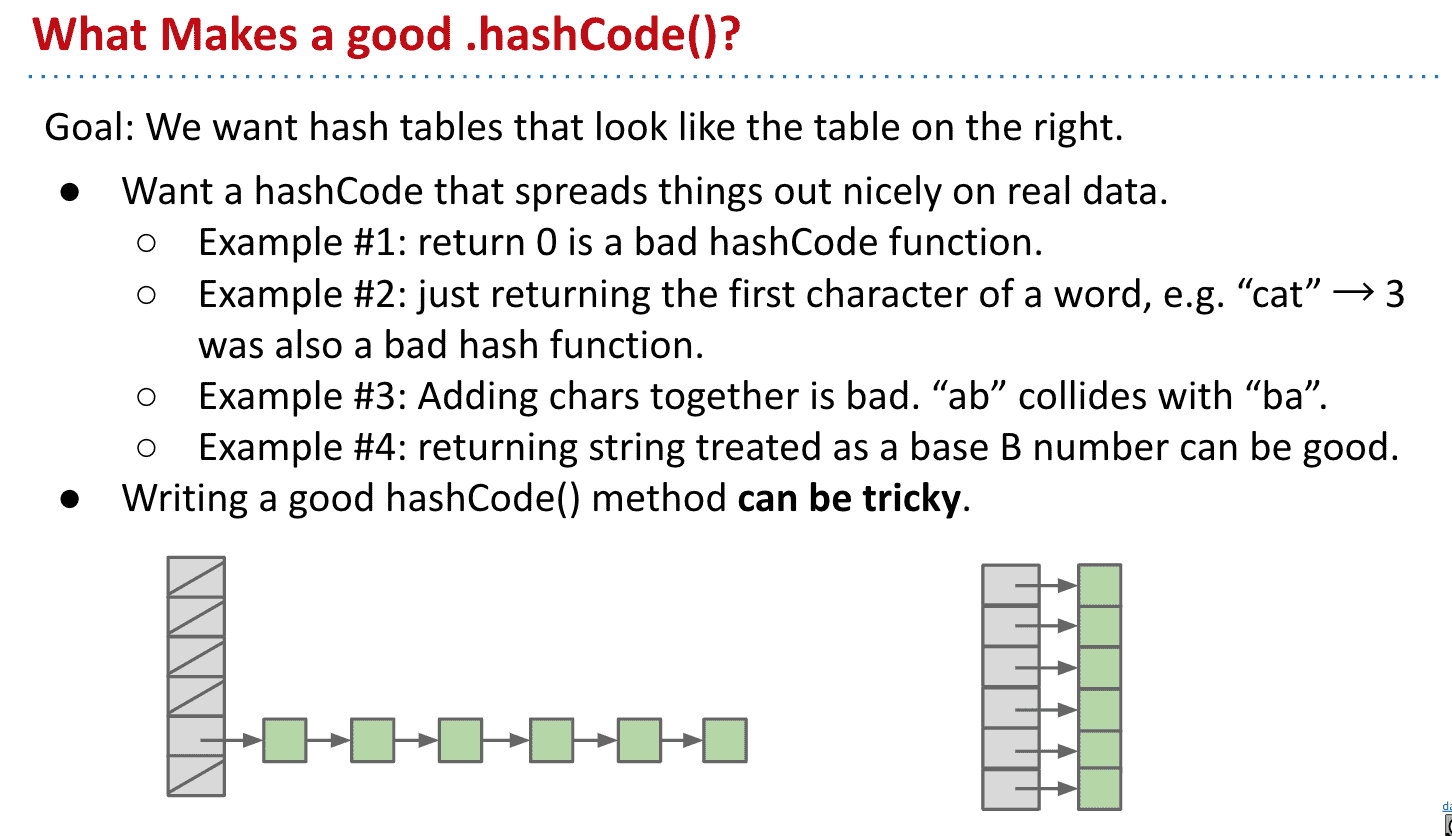
1~3不好的生成hashcode方法举例
String:
Java8中的String的****.hashCode()****实现
主要有两点不同:
- 使用了31作为base,因为不需要是唯一值
- 存储了计算后的散列值,下次使用更快
代码解读:
先读取存储的散列值
如果存在(表示计算过了)就不用计算
把之前的值乘base:31,用i读取String的每一个字母后相加
最后存储计算出的String的散列值

对String的散列值处理
我们之前使用ASCII作为base和Java的比较
虽然base:126能获得唯一值(如果是ASCII strings的话)但是有overflow的问题
因为overflow超过32个字符后,126base只要后面32个字符一样散列值就一样
而由于接下来的处理我们并不太担心不同string的散列值重复

两种散列值计算方式

散列值的计算会有各种问题
好的Base一般选择小的质数(只能被1和本身整除)

为什么要小的质数
Collection:
对于集合的散列值基本就是把集合里每项的散列值遍历并乘base后加在一起
但一般只会计算集合前面一小部分

Recursive Data Structure:
递归的数据结构比如BST就会把节点和两个子节点相加

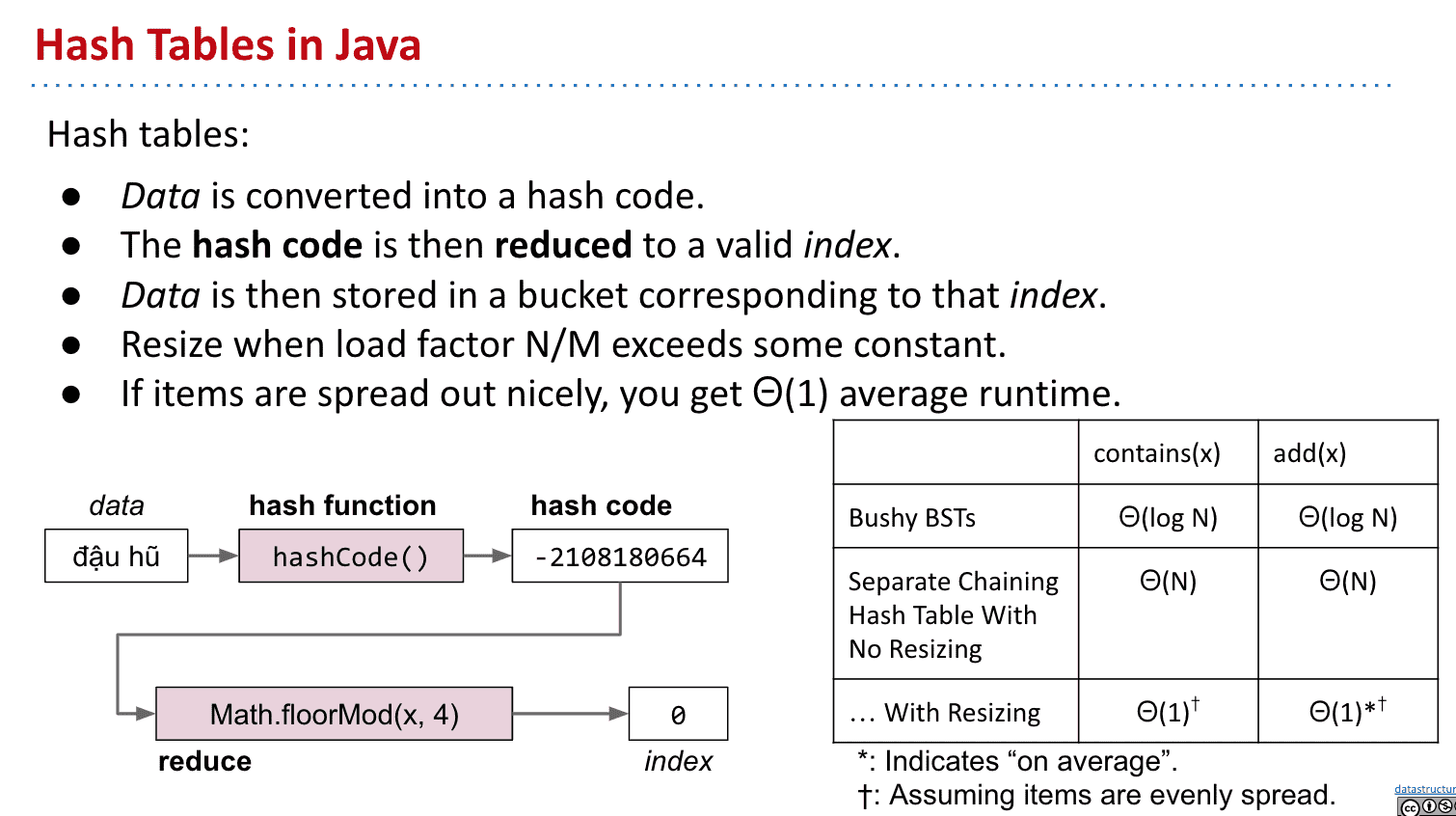
总结Java中的散列表
- 获得数据的散列值
- 把散列值减少到一定位数(比如取余)
- 把数据存到上一部减少后散列值对应index(bucket)
- 如果items(data)/bucket的比到了设定值就扩张bucket
- 如果items分布均匀,运行时间就很理想
Week 8
优先队列 Priority queue
普通的队列是一种先进先出的数据结构,元素在队列尾追加,而从队列头删除。在优先队列中,元素被赋予优先级。当访问元素时,具有最高优先级的元素最先删除。优先队列具有最高级先出 (first in, largest out)的行为特征。通常采用堆数据结构来实现

优先队列的接口
也就是说如果我们需要一堆数据里最大/小的的几个,最高效的办法就是只留下几个的位置,然后每添加一个新的数据就删除原有队列里的最大/小的一个.(也就是只记录最大/小的几个数据)
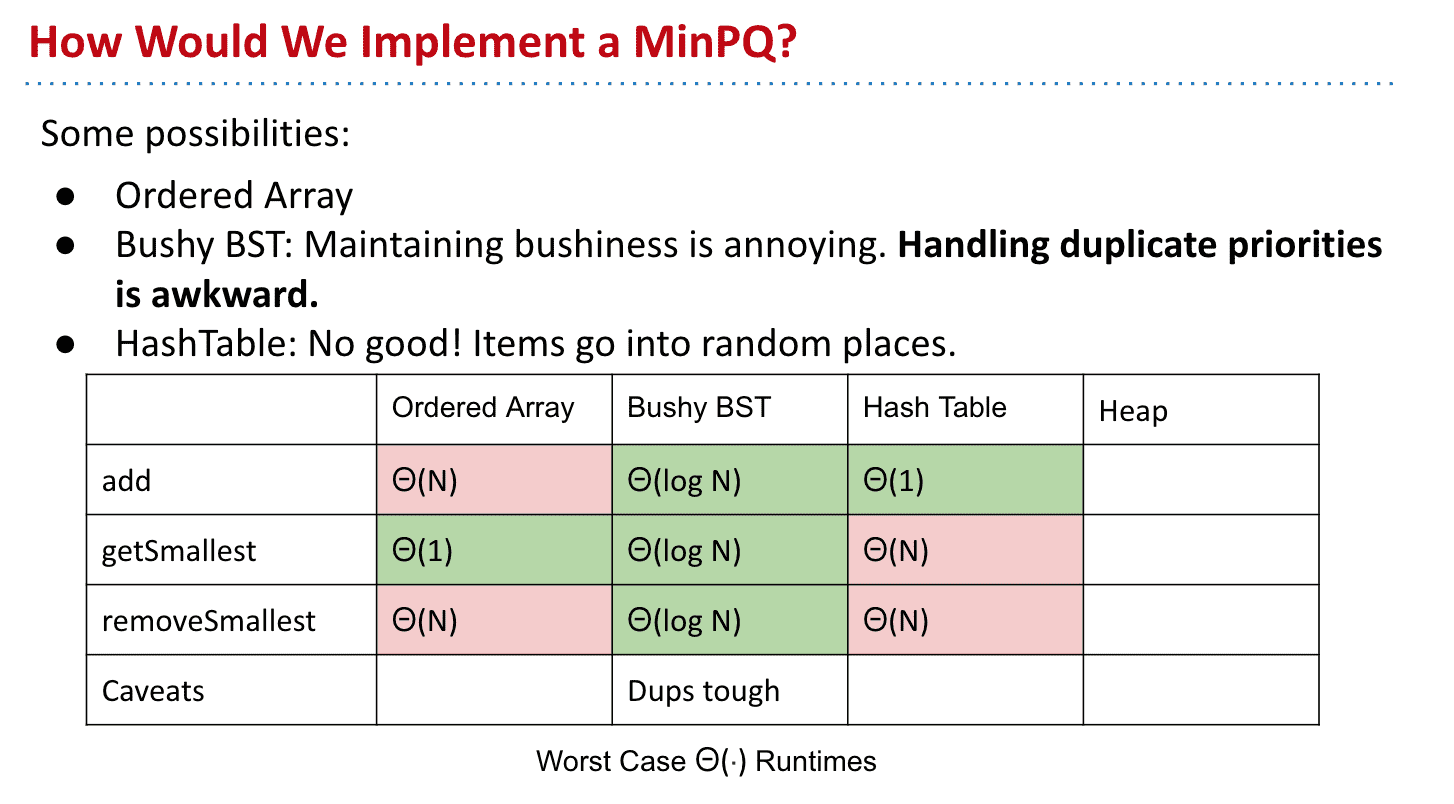
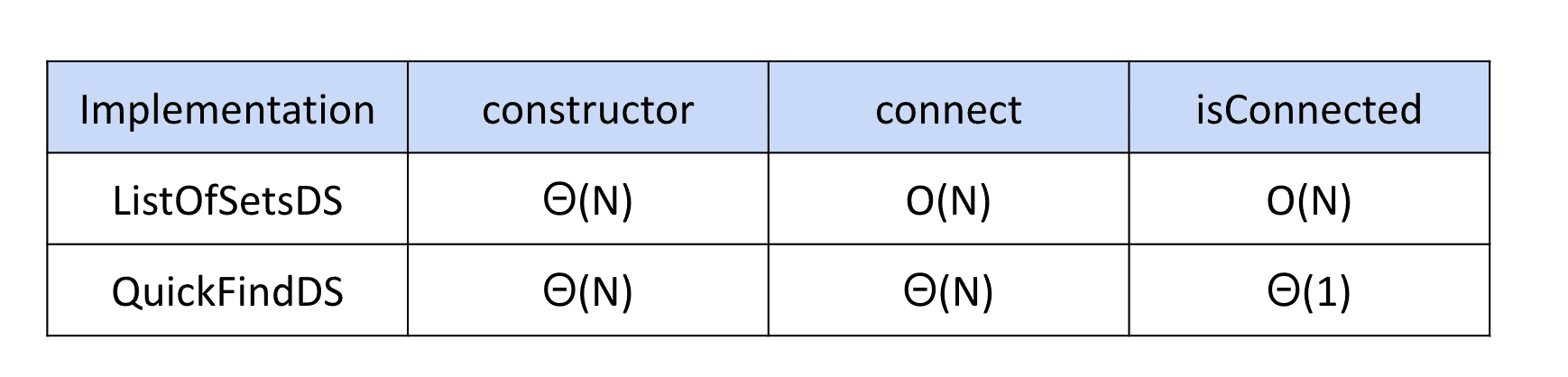
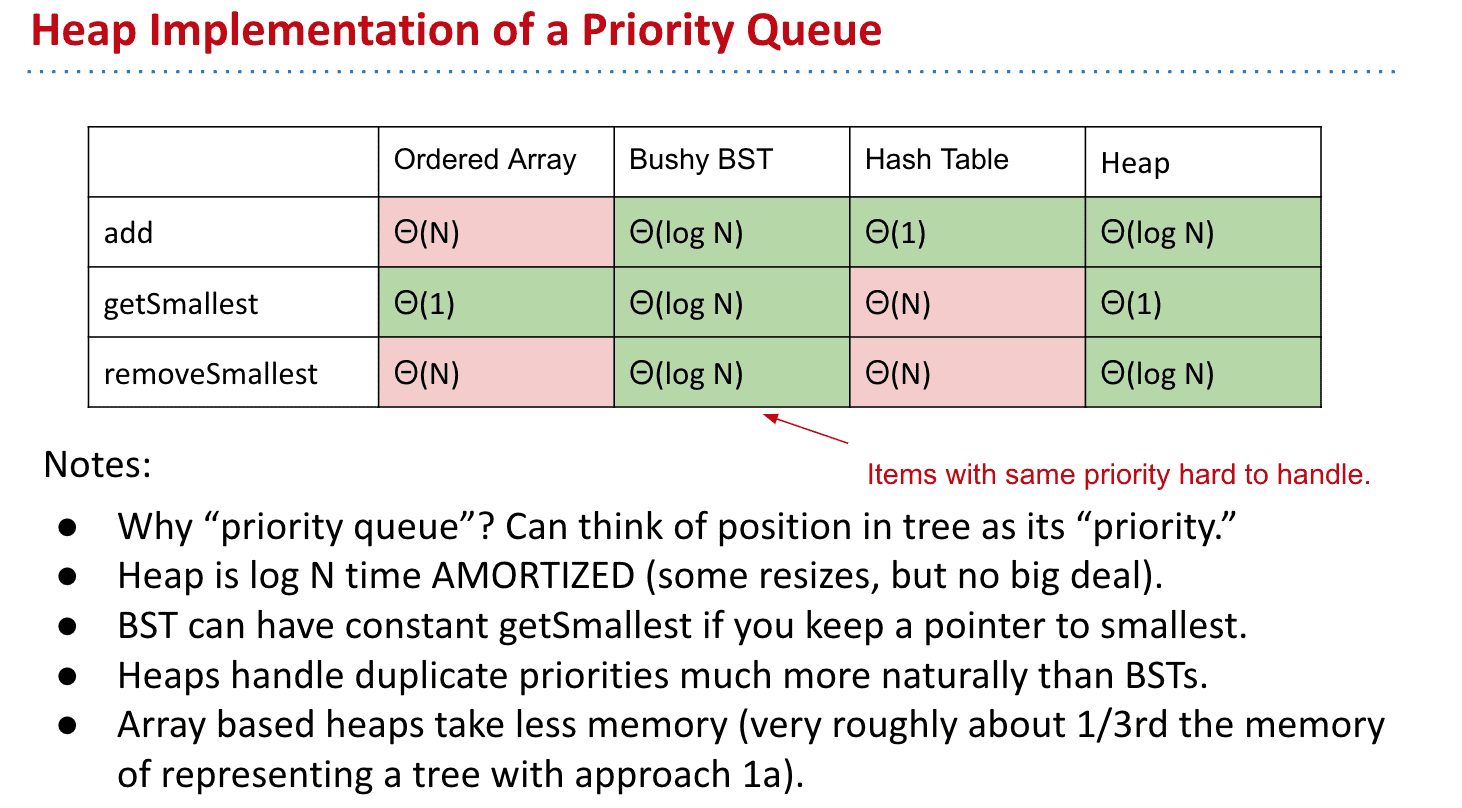
几种优先队列实现方法的运行效率区别
使用不同的结构实现优先队列
有序数组:添加需要遍历整个数组,找到极值很容易,删除的话可能会resize数组所以极端情况也很慢
平衡的BST:所有操作效率都差不多 但还不够快
散列表: 完全不可用,散列表就像数组加上一堆bucket,添加很快但查找效率极低 需要去每个bucket里找极值
因此引入了下一个数据结构概念:Heap
堆 Heaps
非常适合用于实现优先队列,本质上是一种特别的二叉树
注意区分抽象类型和实现的区别
堆是计算机科学中的一种特别的完全二叉树(bushy或者说平衡,除了最后一层都是满的,最后一层也只在右边缺)。若是满足以下特性,即可称为堆:“给定堆中任意节点P和C,若P是C的母节点,那么P的值会小于等于(或大于等于)C的值”。若母节点的值恒小于等于子节点的值,此堆称为最小堆(min heap);反之,若母节点的值恒大于等于子节的值,此堆称为最大堆(max heap)。在堆中最顶端的那一个节点,称作根节点(root node),根节点本身没有母节点(parent node)。
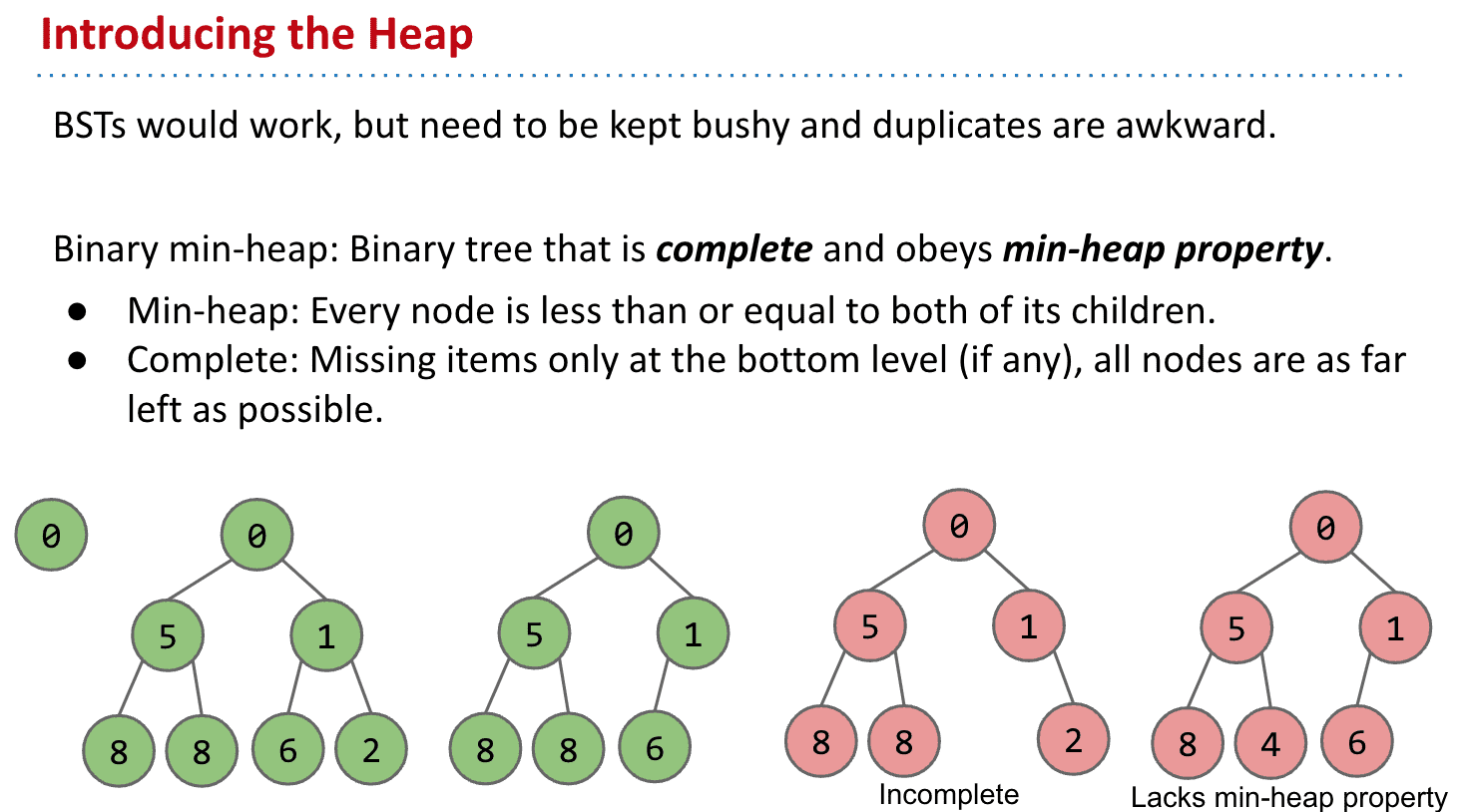
第三个不完整,第四个没用遵守子节点小于/等于的性质
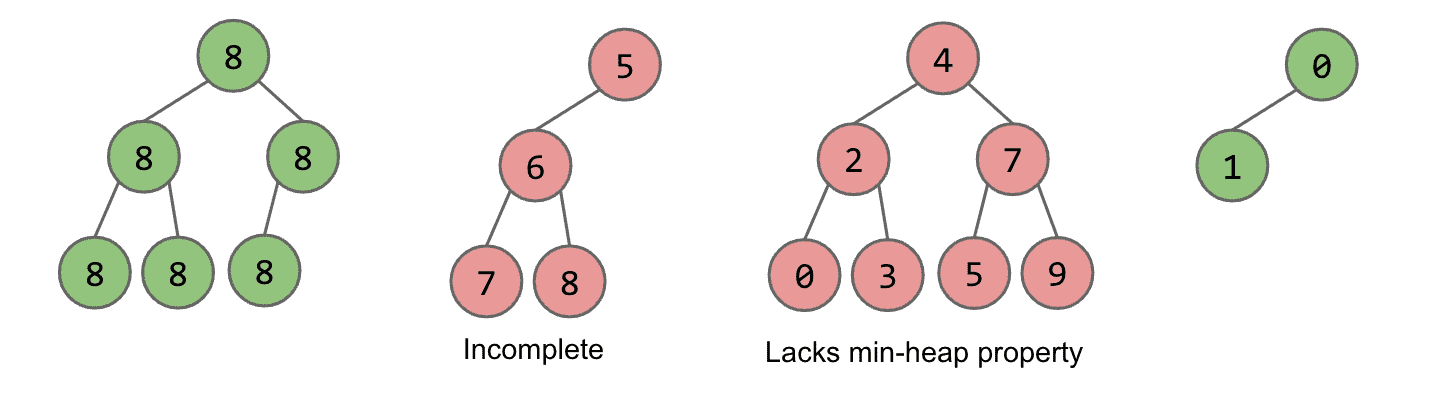
Binary min-heap
是一种特殊的堆,有两个性质
- Binary min-heap的每一个节点都等于或者小于它的两个子节点
- 只会在最后一层缺少节点(并且是右边的节点),其他层都是满的
操作:
-
getSmallest()
另外可以注意到,Binary min-heap的最小值总是root,所以
getSmallest()很快速! -
add()
比如要在这样一个heap里add(3)
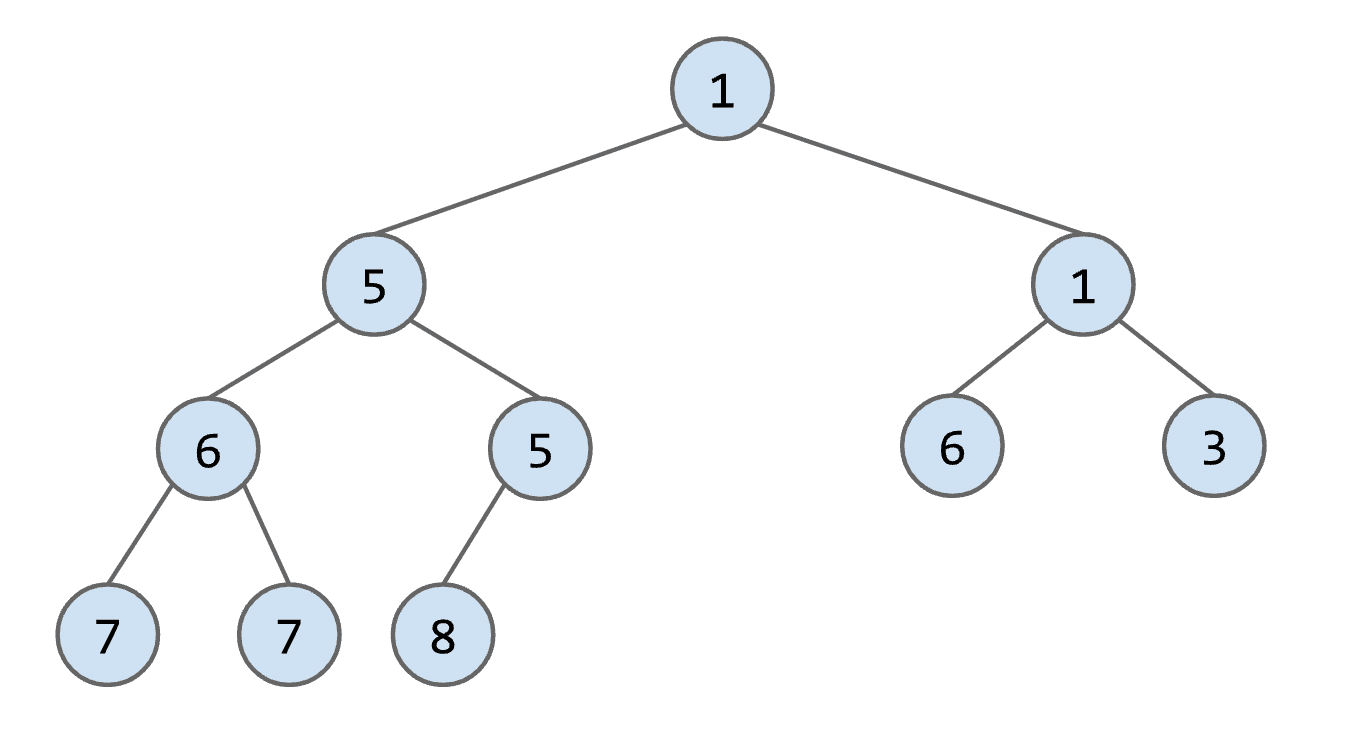
首先要找个一个有缺口的地方(也就是最后一层右边是空的节点)以满足我们左边是满的的要求
然后放下这个要添加的节点
再将这个节点与它的父节点比较(由于是min-heap所以越小越靠近root)如果节点更小就与父节点交换
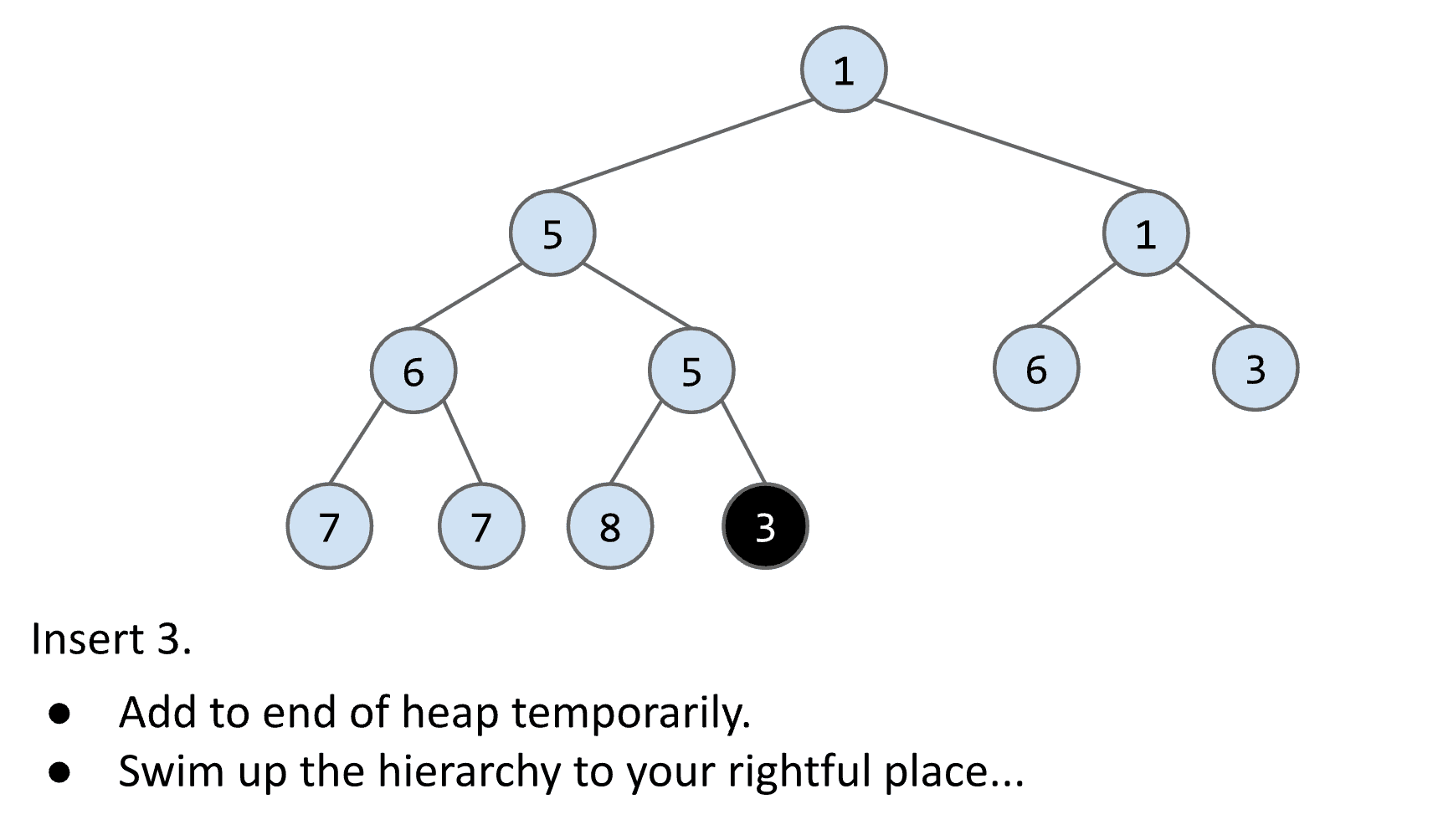
经过各种交换上升后最终这个添加的节点,放置到了合适的位置
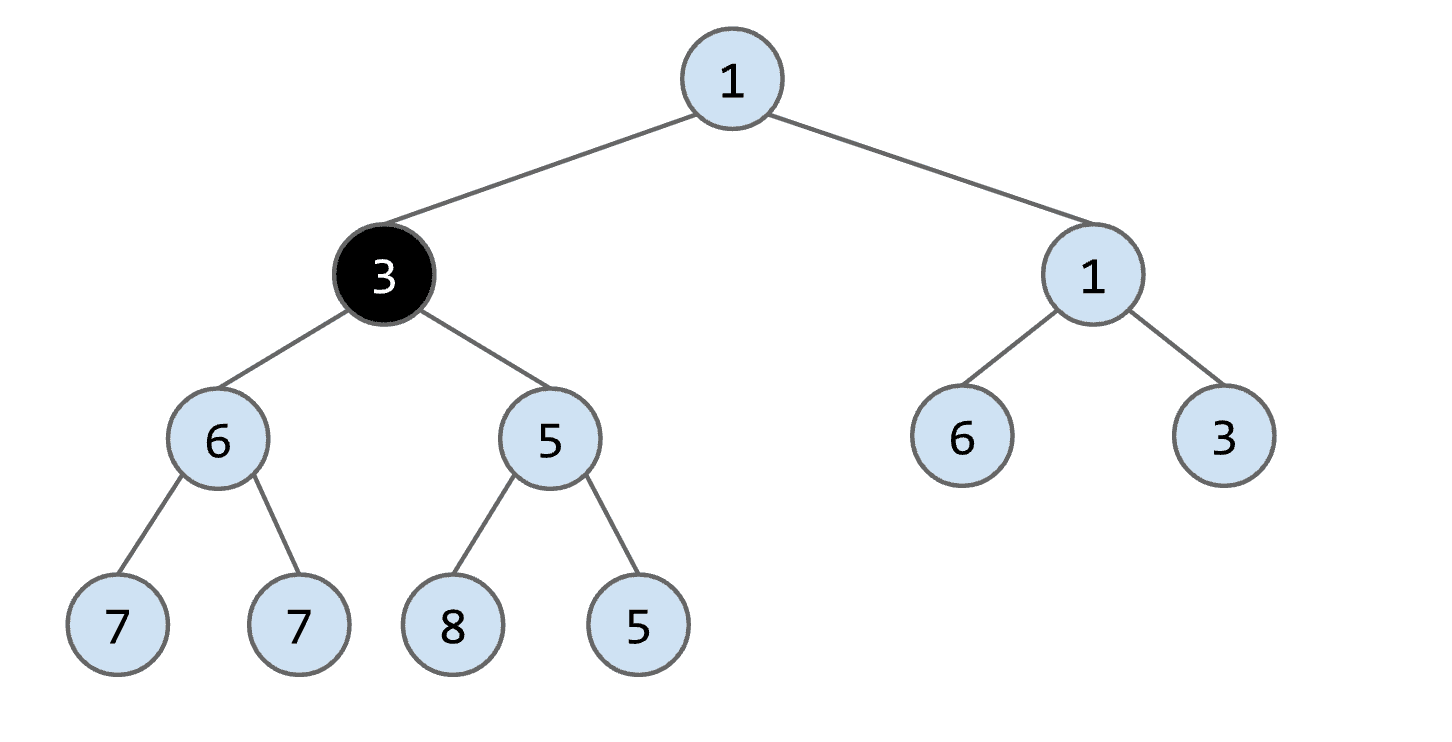
- removeSmallest()
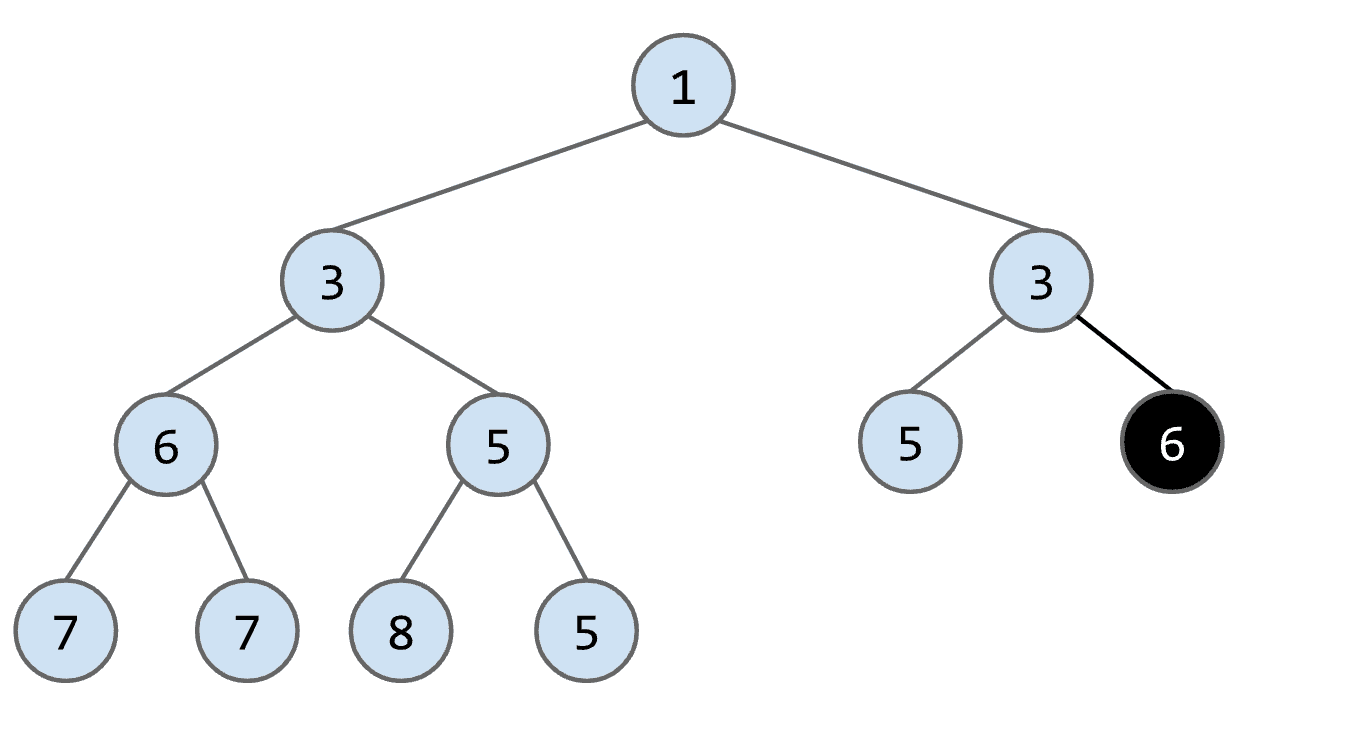
基本就是add的反向操作,记住在Binary min-heap中最小的节点就是root
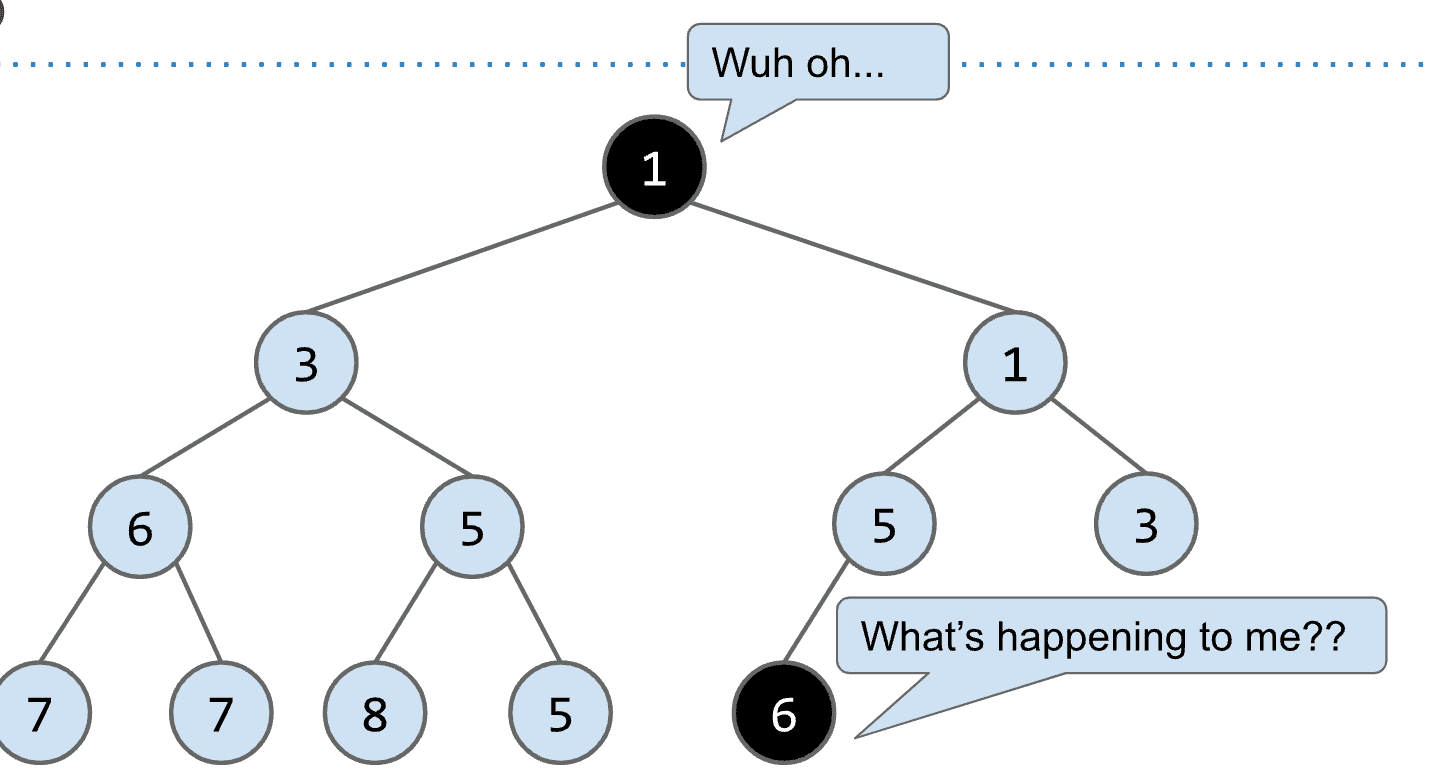
删除root后再把最后一个节点移动到原本root的位置
再将这个新的“root”与子节点比较、交换
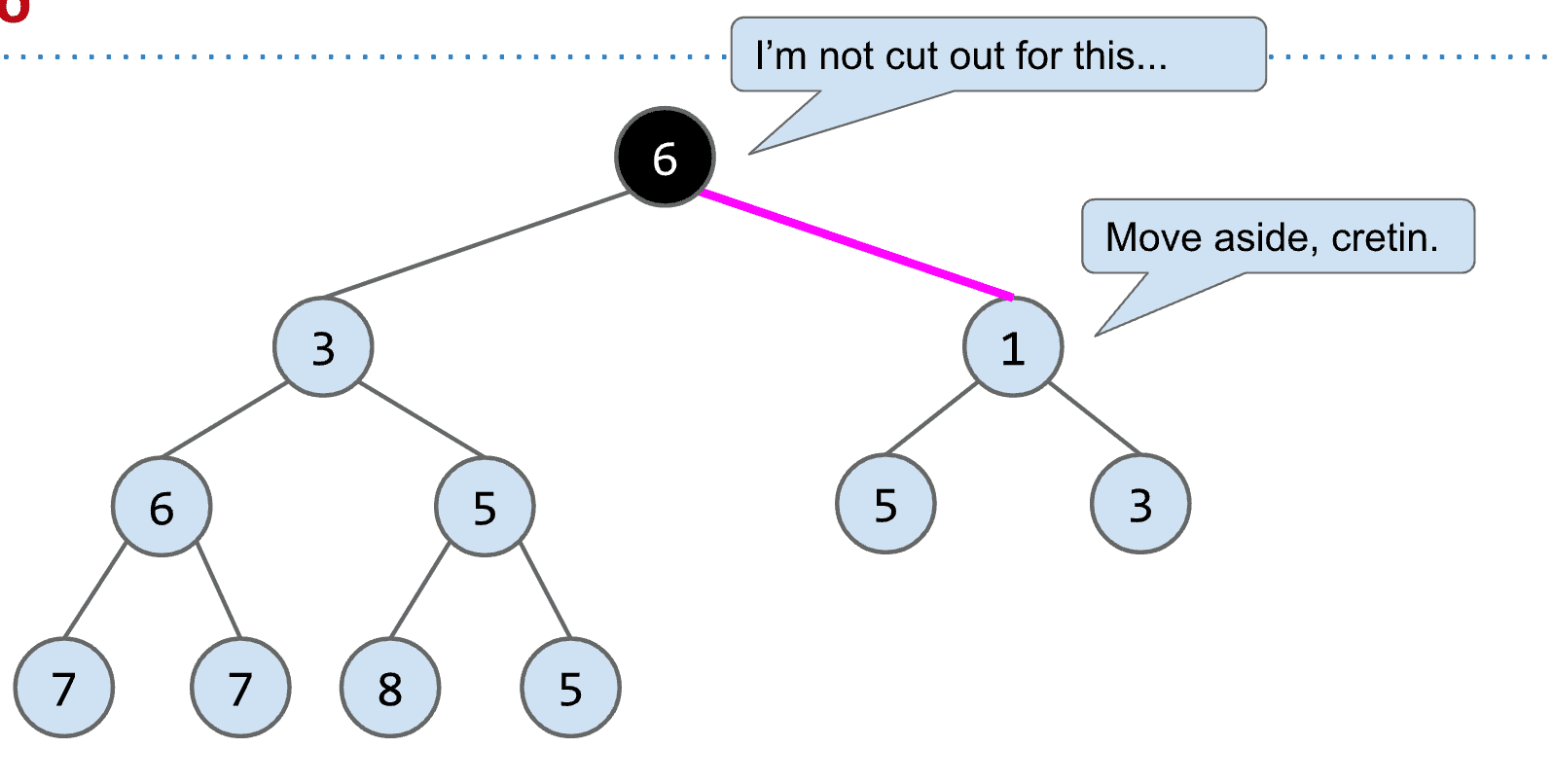
经过不断的下降、交换后替代原本root的节点也到了正确的位置
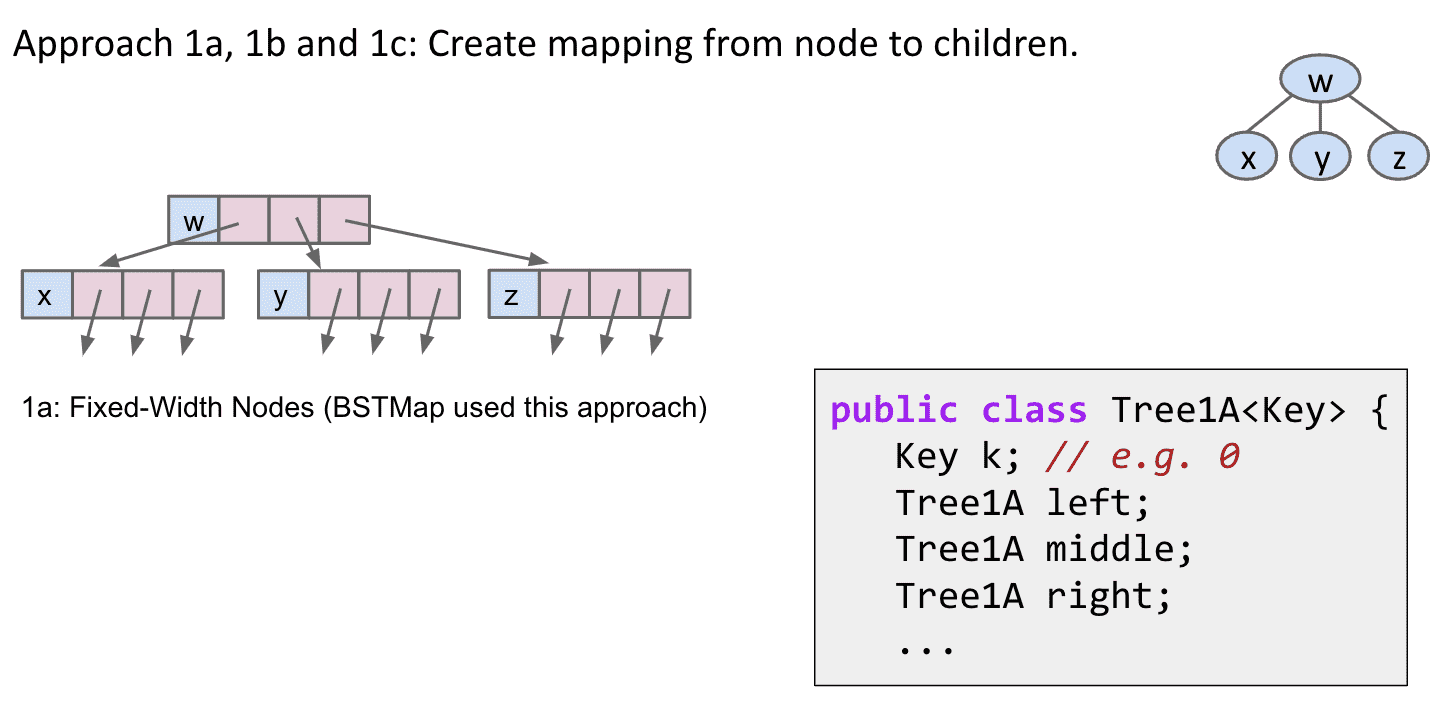
1a:比较直观的一种,和BSTMap差不多 存下本身的值和子节点的位置
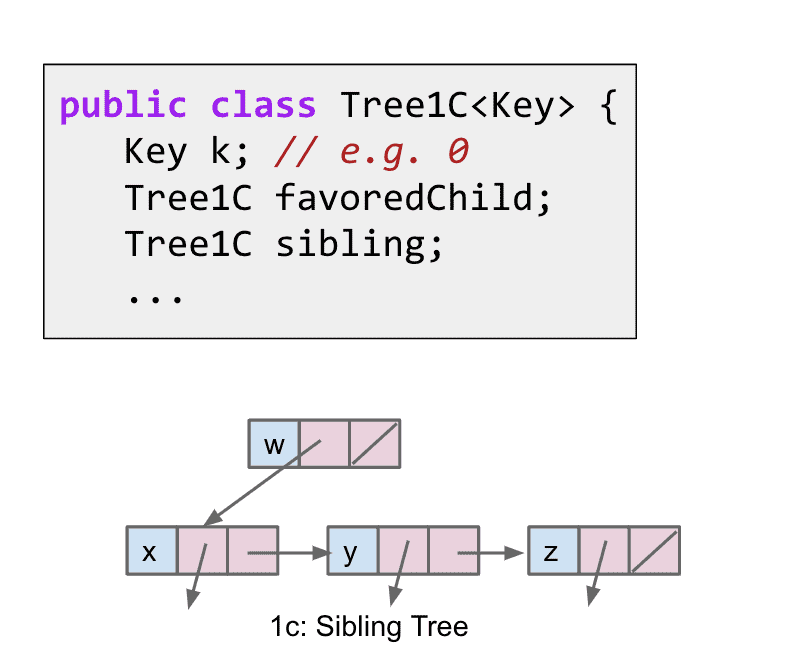
1c.每个节点有一个指向子节点和一个指向“兄弟”的指针
2.使用数组存储key和父节点
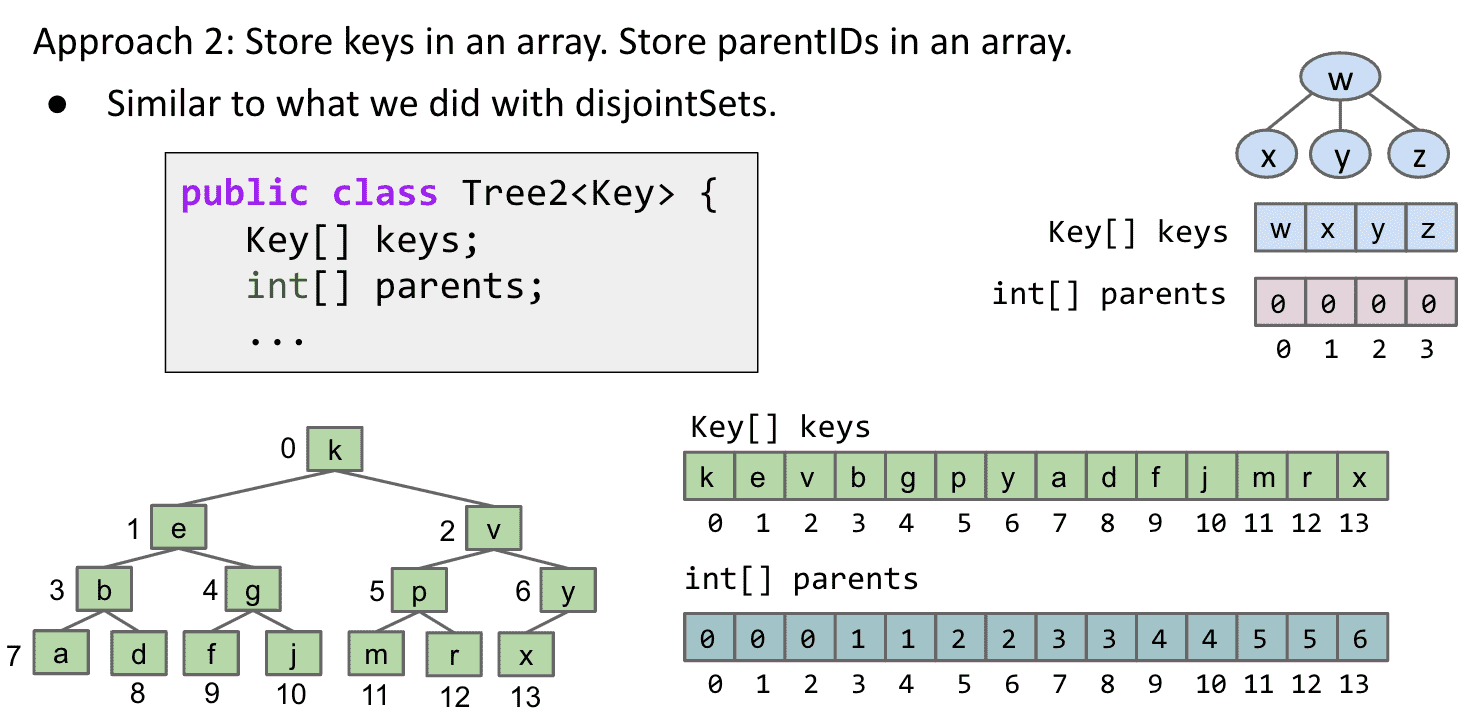
注意存储父节点的数组,在树完整有顺序的情况下,就是1 1 2 2 3 3 4 4的形式
这一个的实现和disjointSets的使用Quick Union组建(改进) 有点类似,不显式地存储
用两个数组一个存储它的值一个存储它的父级节点
如果是一个完整的tree并且按照了顺序,那么它的parents数组是有顺序的
3.由于这个树很标准,可以只存储key不存储父节点
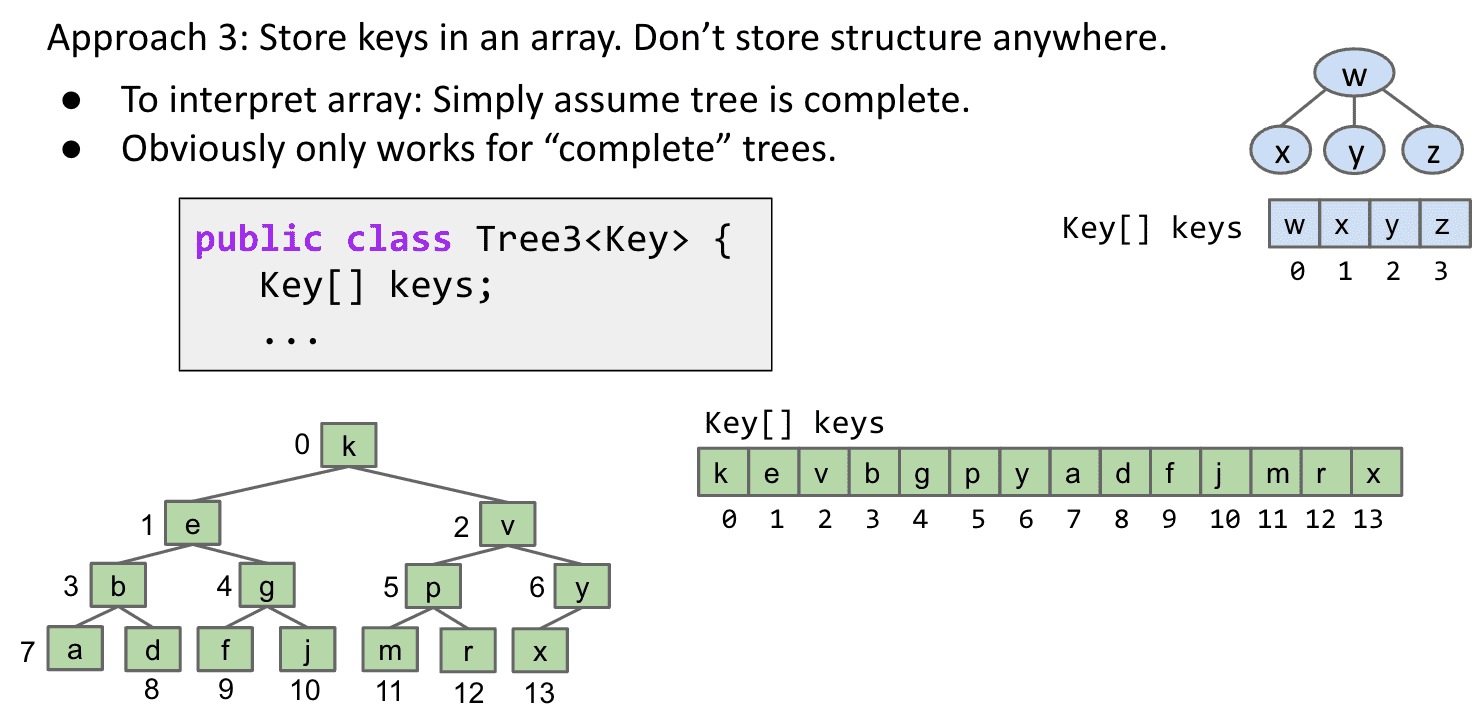
所以在完整有顺序的tree的情况下(就像我们的BMT),我们可以完全抛弃父节点的数组
要找到父节点位置也很简单,Java “/”会只保留整数,所以可以使用(k - 1) / 2得到父节点位置(root可能不适用)
这也是现实中Heaps的实现方法,由于没有各种link所以速度很快!
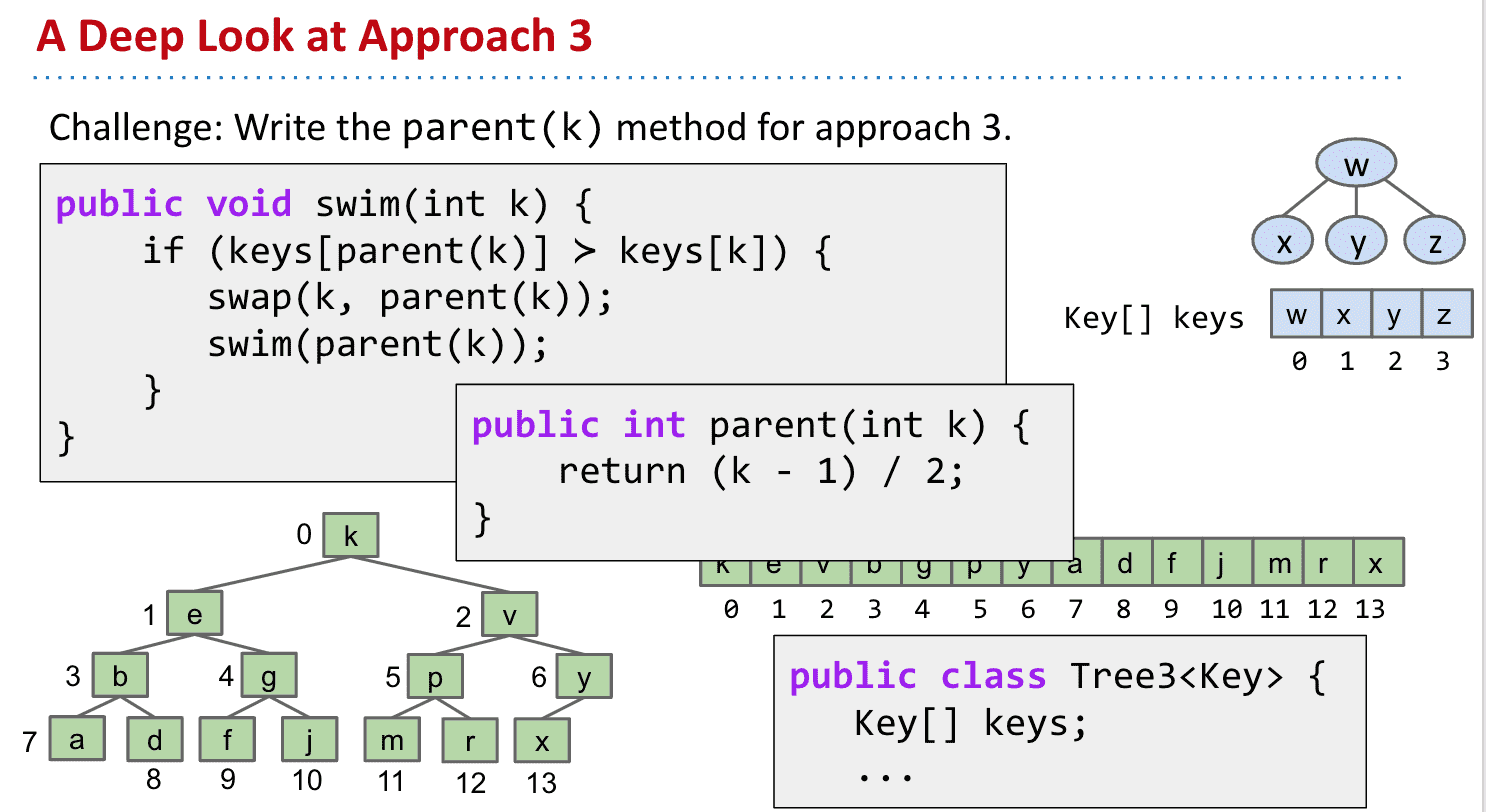
似乎是节点位置的算法
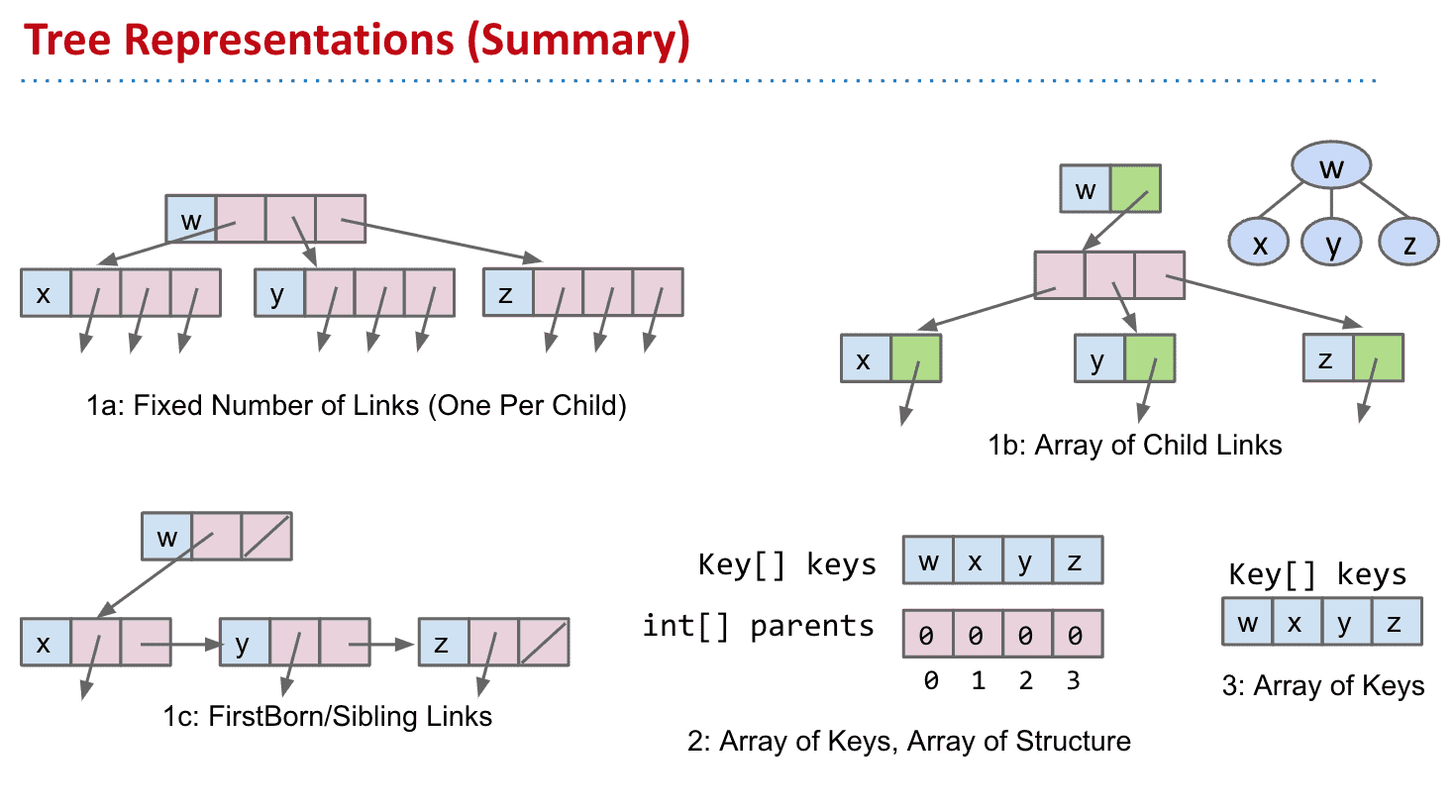
几种实现树的方法总结
3b.留空让计算更高效(教科书使用)
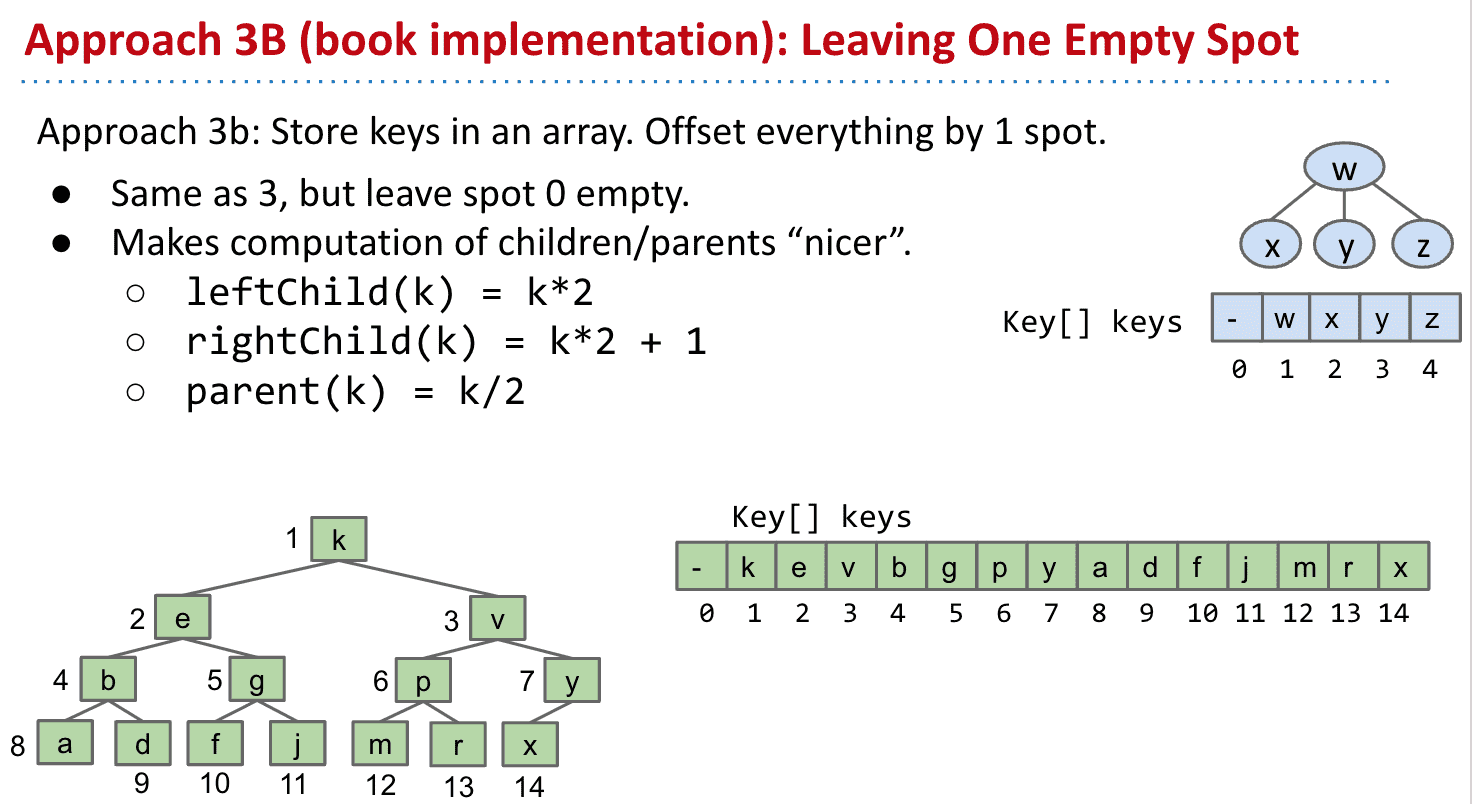
无需每次计算都减1,性能提升 类似于哨兵节点

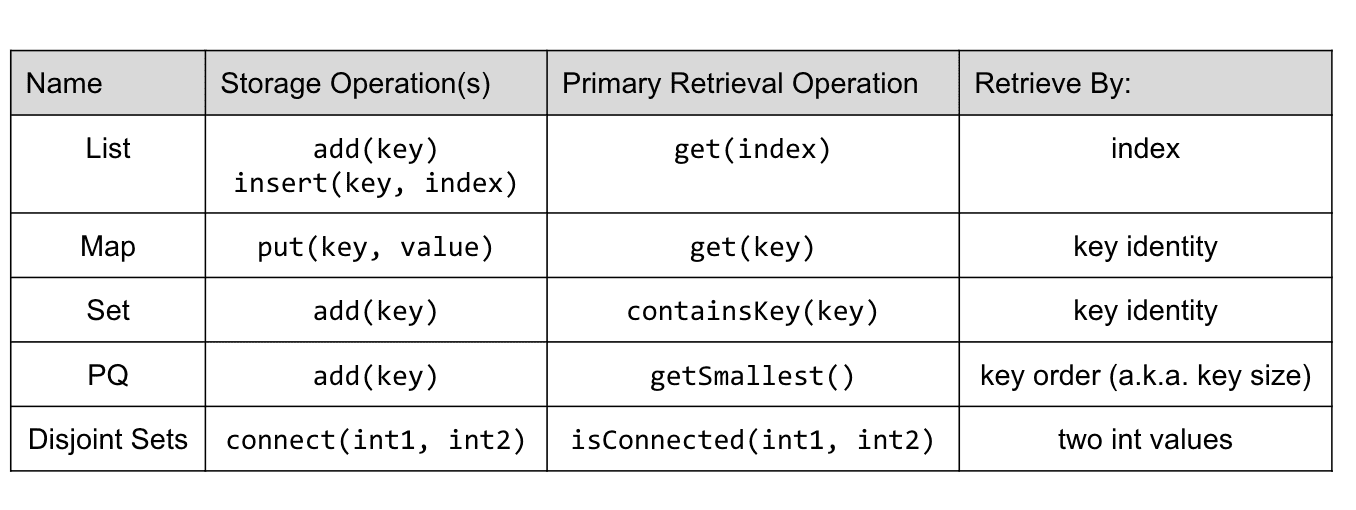
数据结构小总结
几乎所有的数据结构只为了解决一件事:搜索,
也就是找到数据,而不同的结构在不同的环境下性能和实现难度不一样
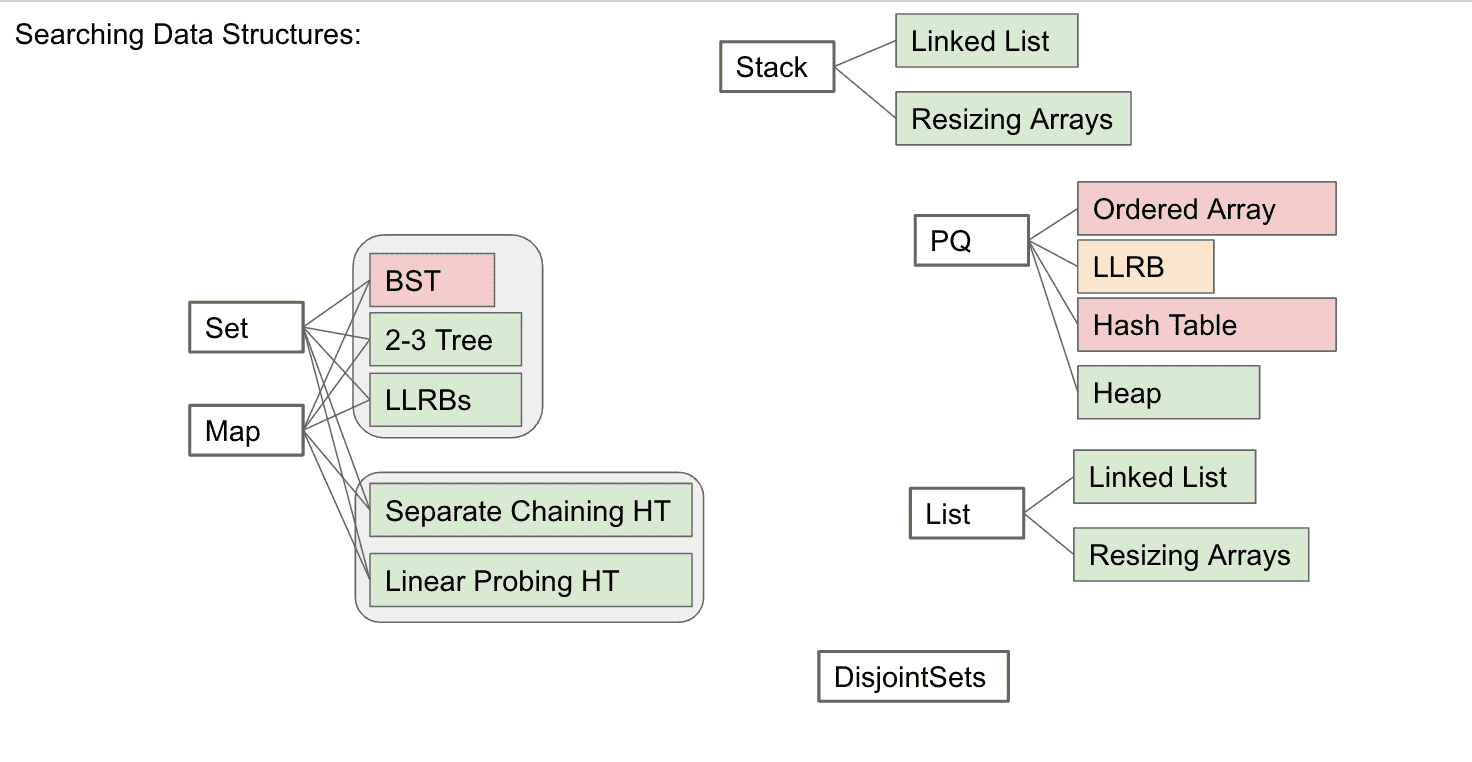
红色是不太好的实现方式
树的遍历
tree traversa(tree iteration)
和lists不同,遍历一个树不是只有前进后退两种操作,而是有很多种方式来访问每一个node
几种树的遍历方式:
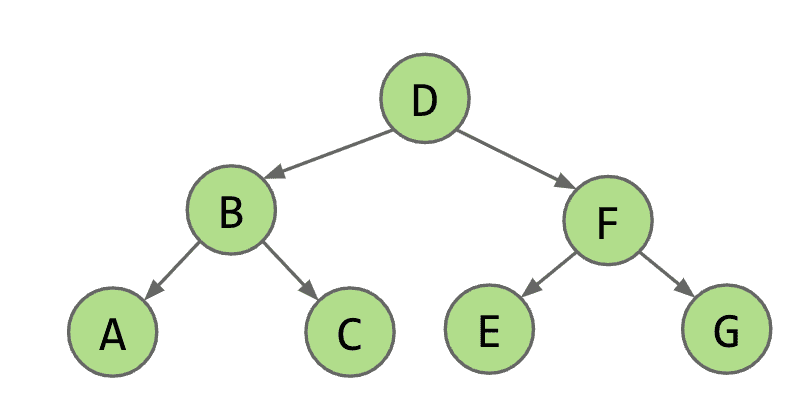
- 层序遍历( Level Order)
按照从上到下然后从左到右的顺序来遍历(就像阅读一样),顺序: DBFACEG
- 深度优先搜索 (Depth-first search) or DFS
按照深度优先,下面的节点比上面的先遍历,分为三种类型:
-
先序遍历 Preorder

顺序:DBACFEG
先打印出父节点再打印子节点,并且先左后右
Preorder很适合作为文件目录打印(下图左)
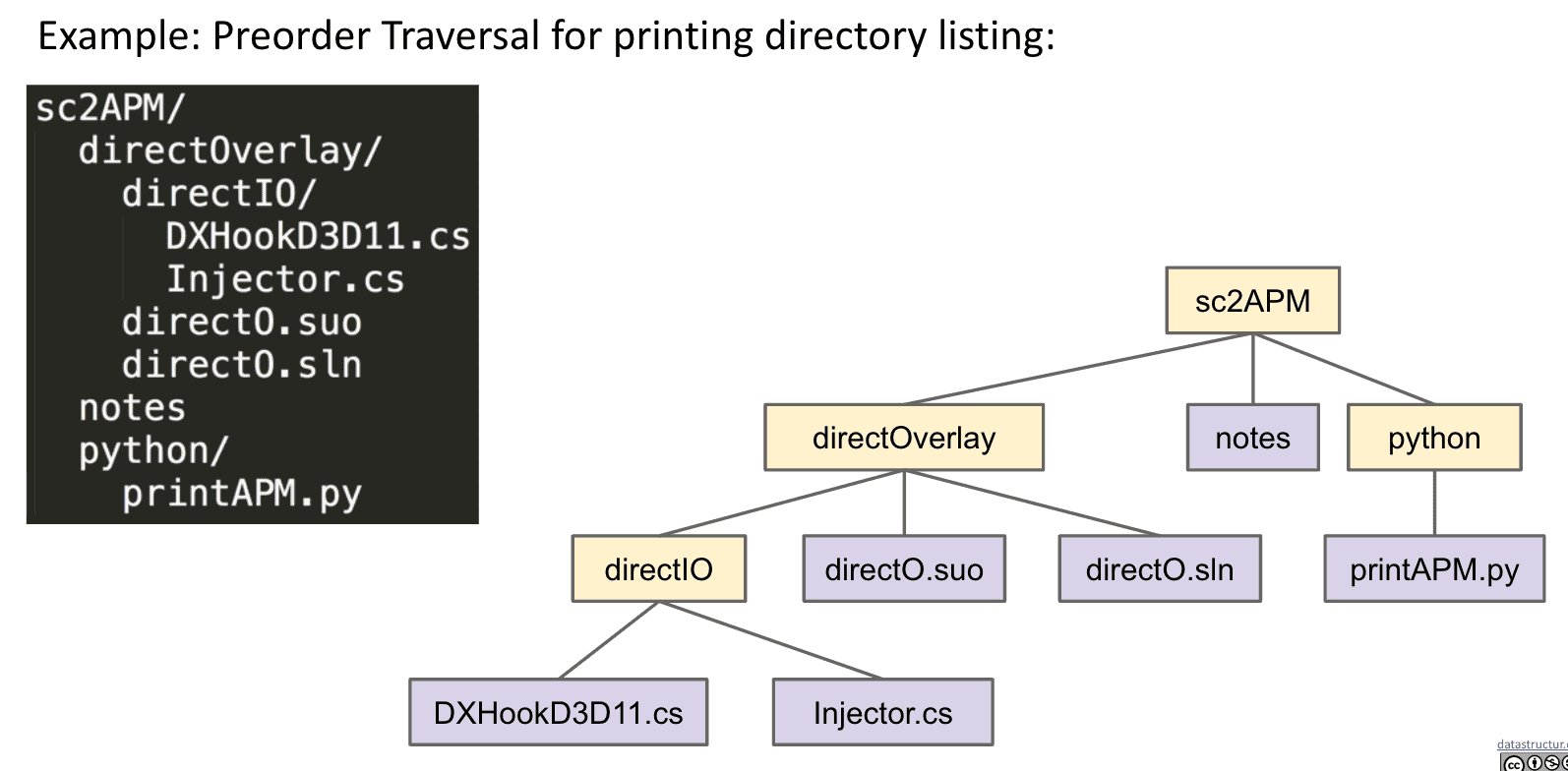
通过缩进来表示子节点
-
中序遍历 Inorder

顺序:ABCDEFG
和真正的顺序一样,先左子节点再中节点再右子节点
-
后序遍历 Postorder

顺序:ACBEGFD
基本上就是从下往上遍历
Postorder适合用于计算文件夹大小,下方的文件大小一步步向上汇总
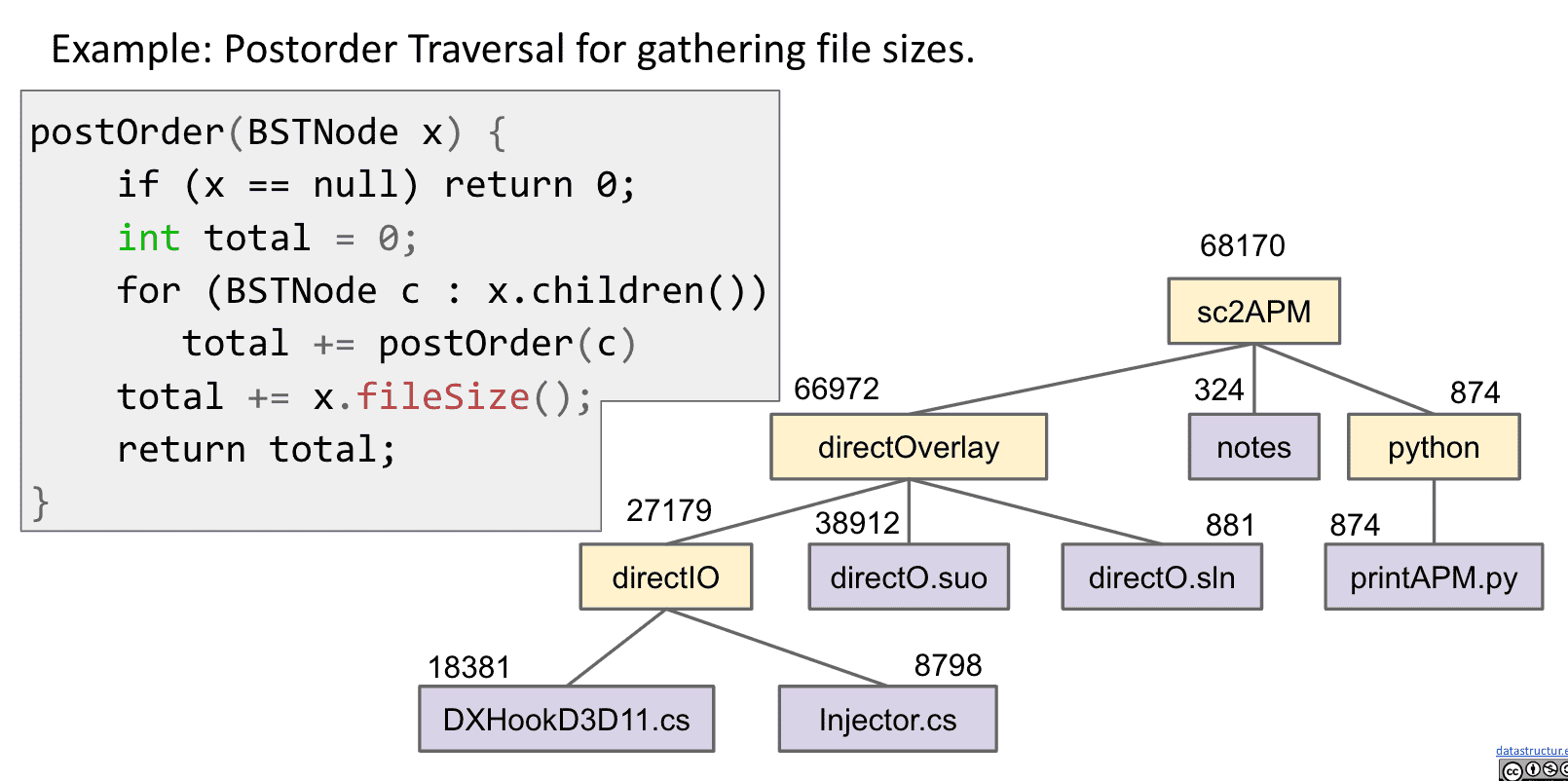
图 Graphs
一堆节点,并且节点之间有0或更多edges连接着节点们,但edges不能连接节点自己到自己,也没有多条edges连接着同样的两个节点
树很适合表示层次关系,但还有不是层次的关系,比如地铁的线路 从一个站点到另一个站点可能有很多种不同的方式
tree就是一种没有Cycles和每个vertex(node)相连的Graphs
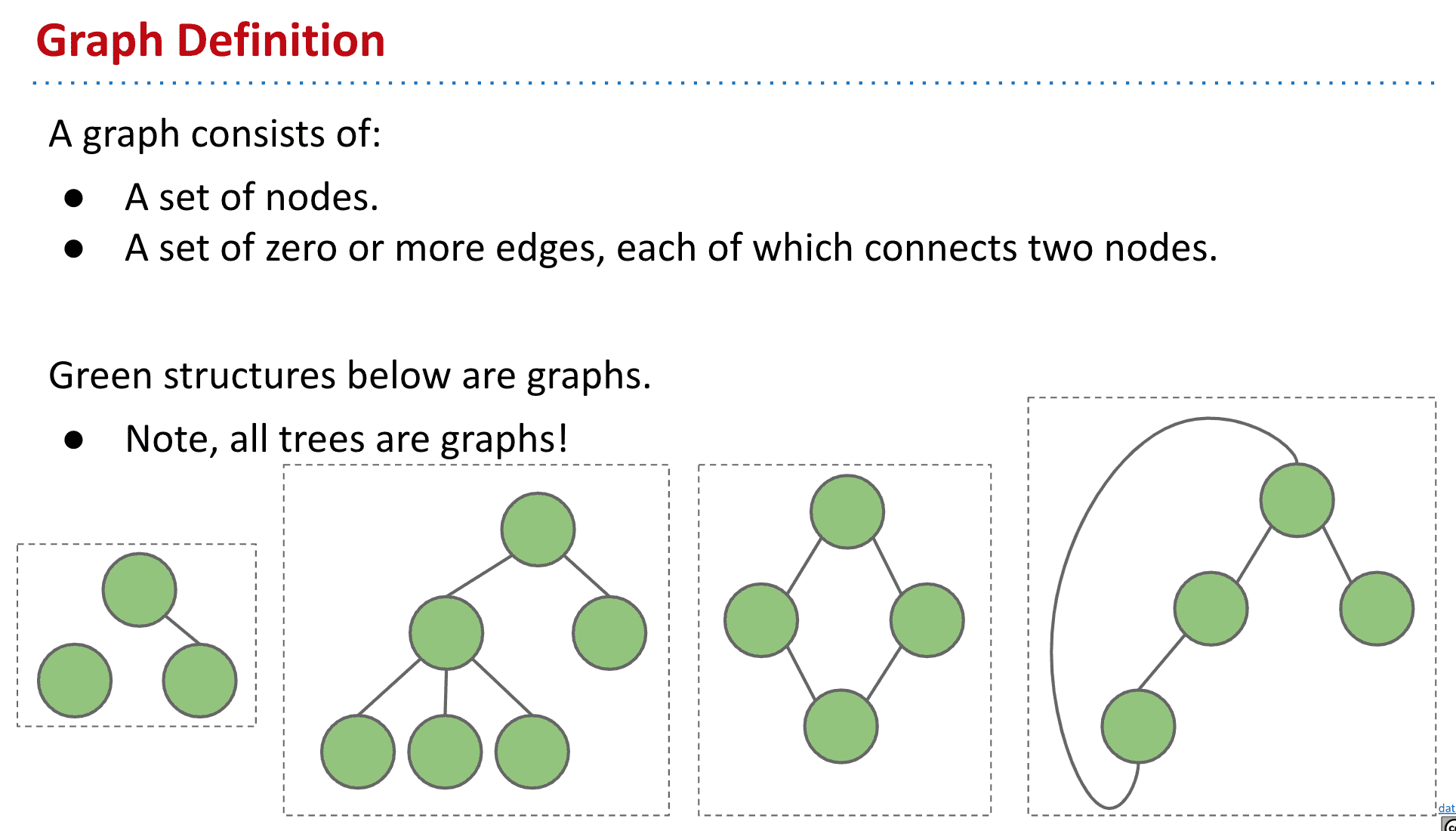
图2是树,并且所以树都属于图
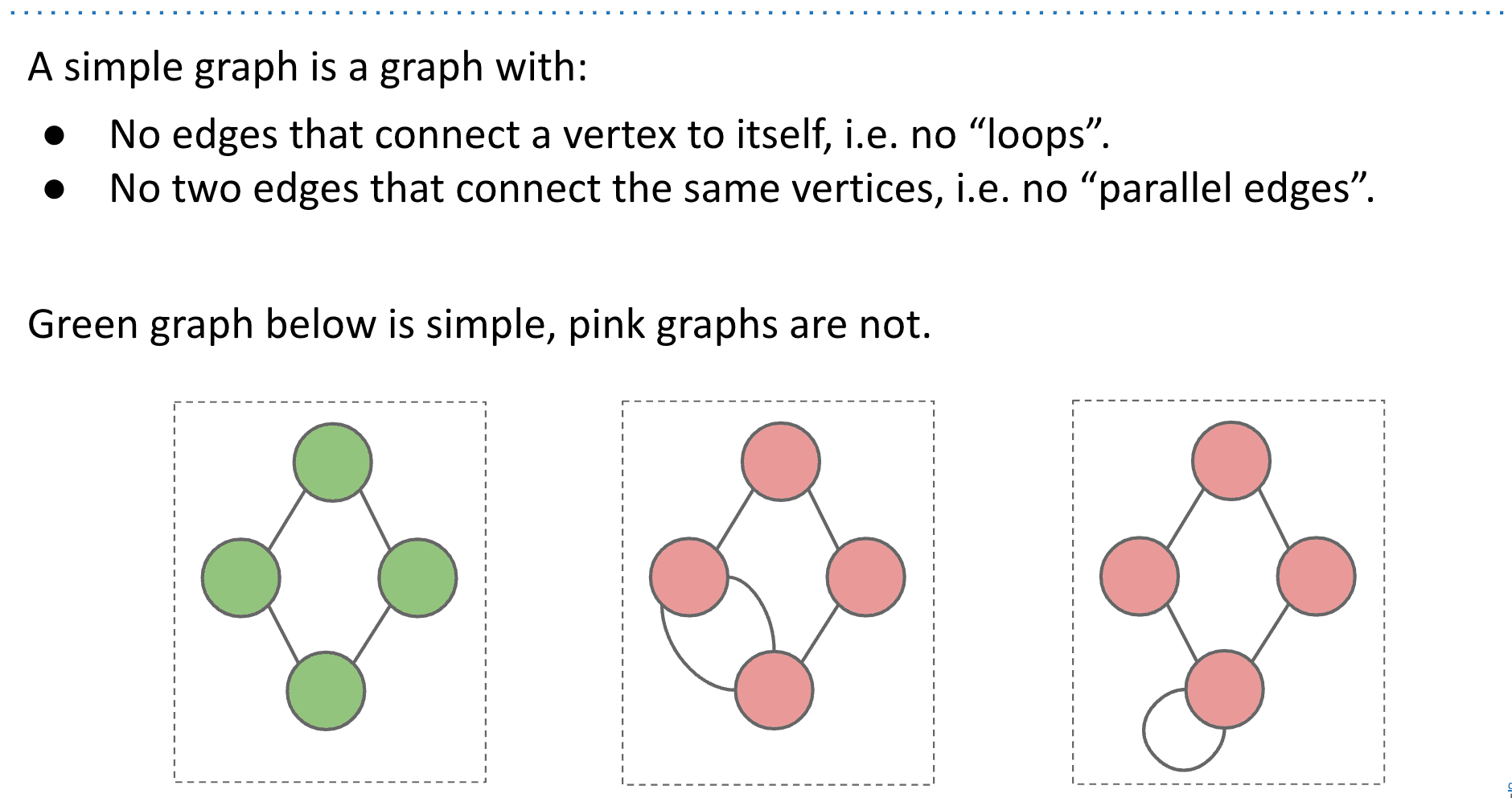
绿色的也称为简单图simple graph,本课里的graph都是simple graph
Graph的类型
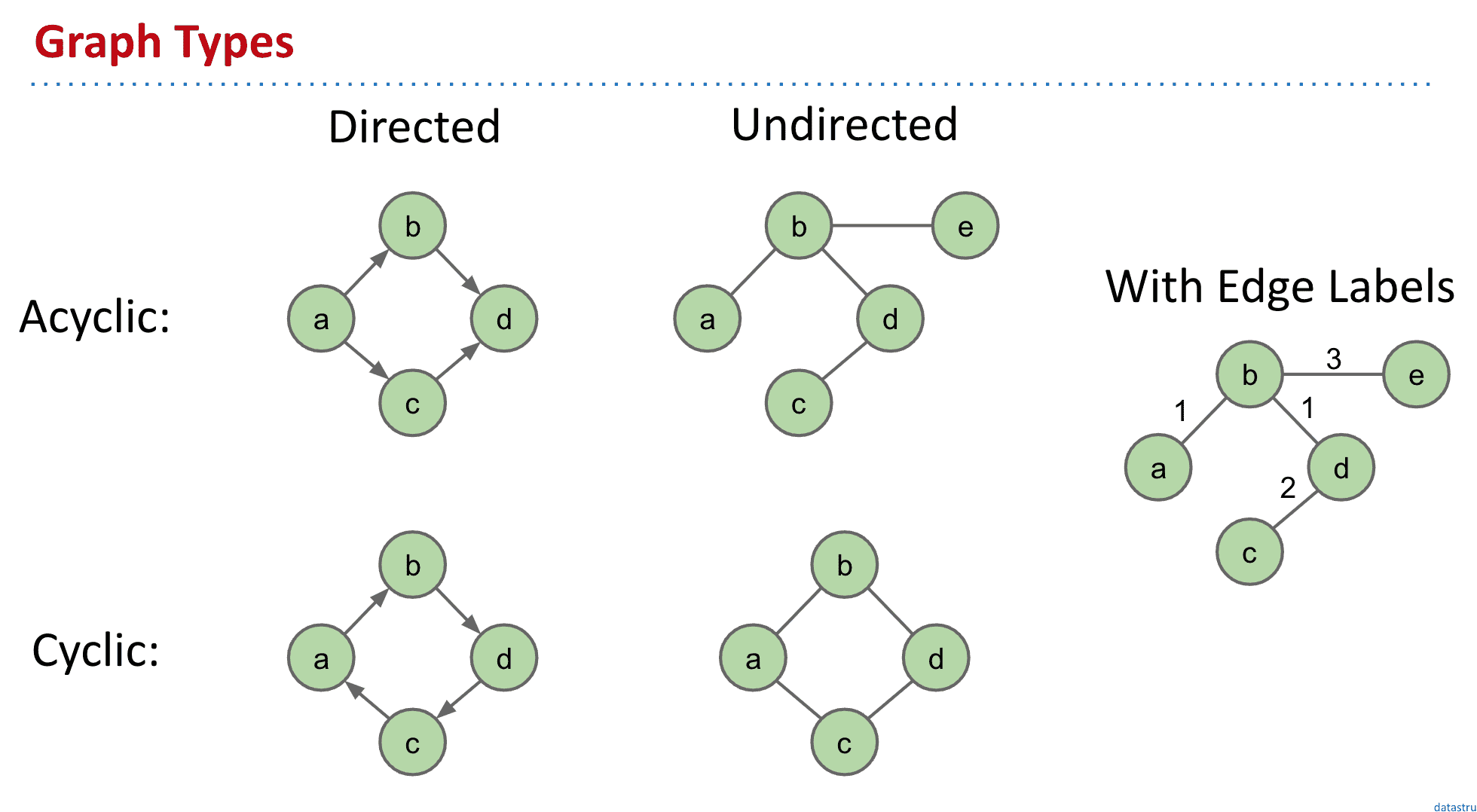
Acyclic非循环、Cyclic:循环、Directed:有指向
Graph的术语
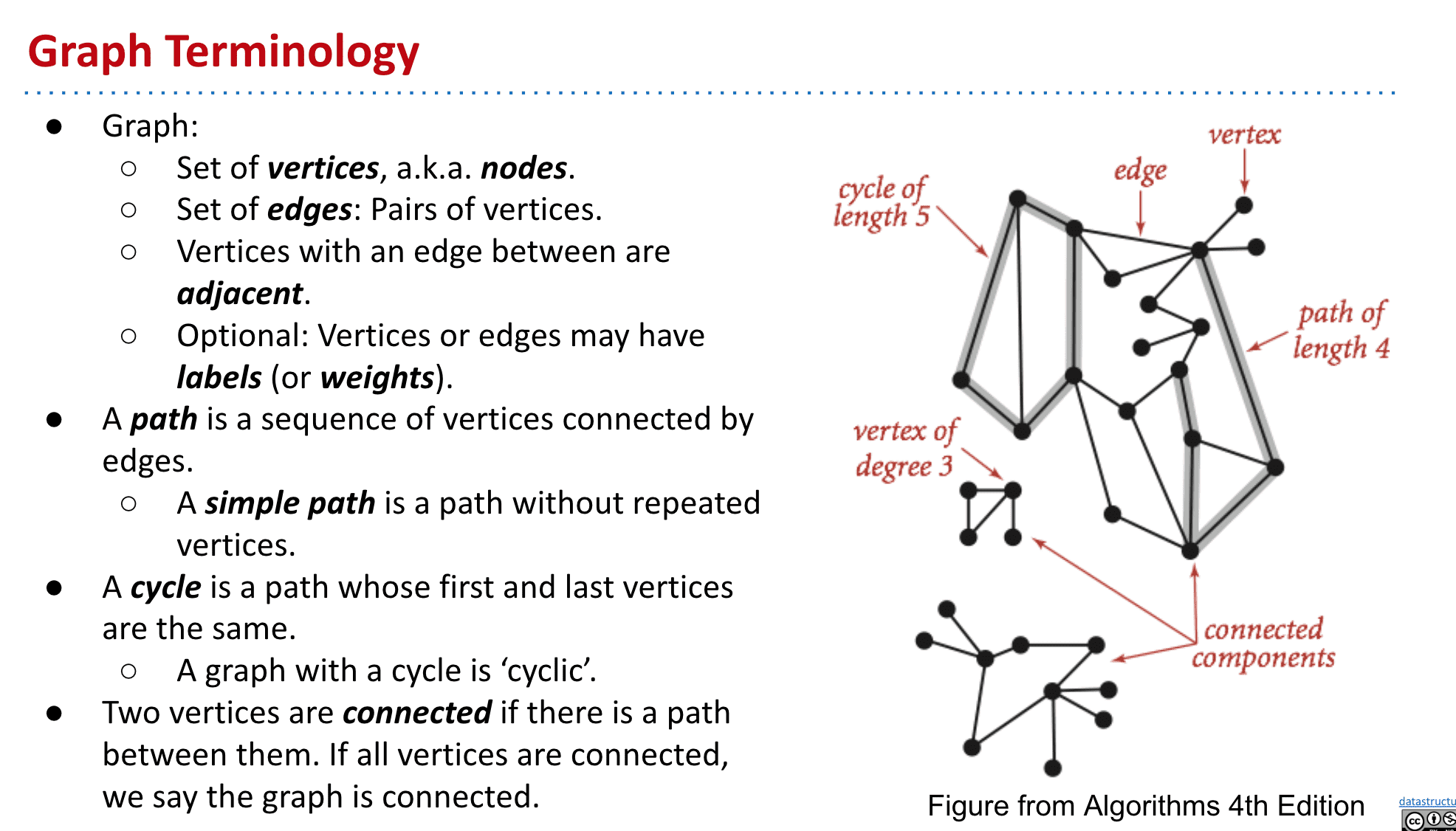
Graph相关的问题
只作为展示Graph本身的深度用


深度优先遍历 (Depth-first traversal)
解决s-t Connectivity问题
通过遍历把s相邻的节点都判断是否等于t,这样遍历下去如果有一个相等(也就是s-t相连了)就返回ture,另外会给当过s的节点做上标记以防止无限循环比如0的邻居是1,1的又是0这样来来回回
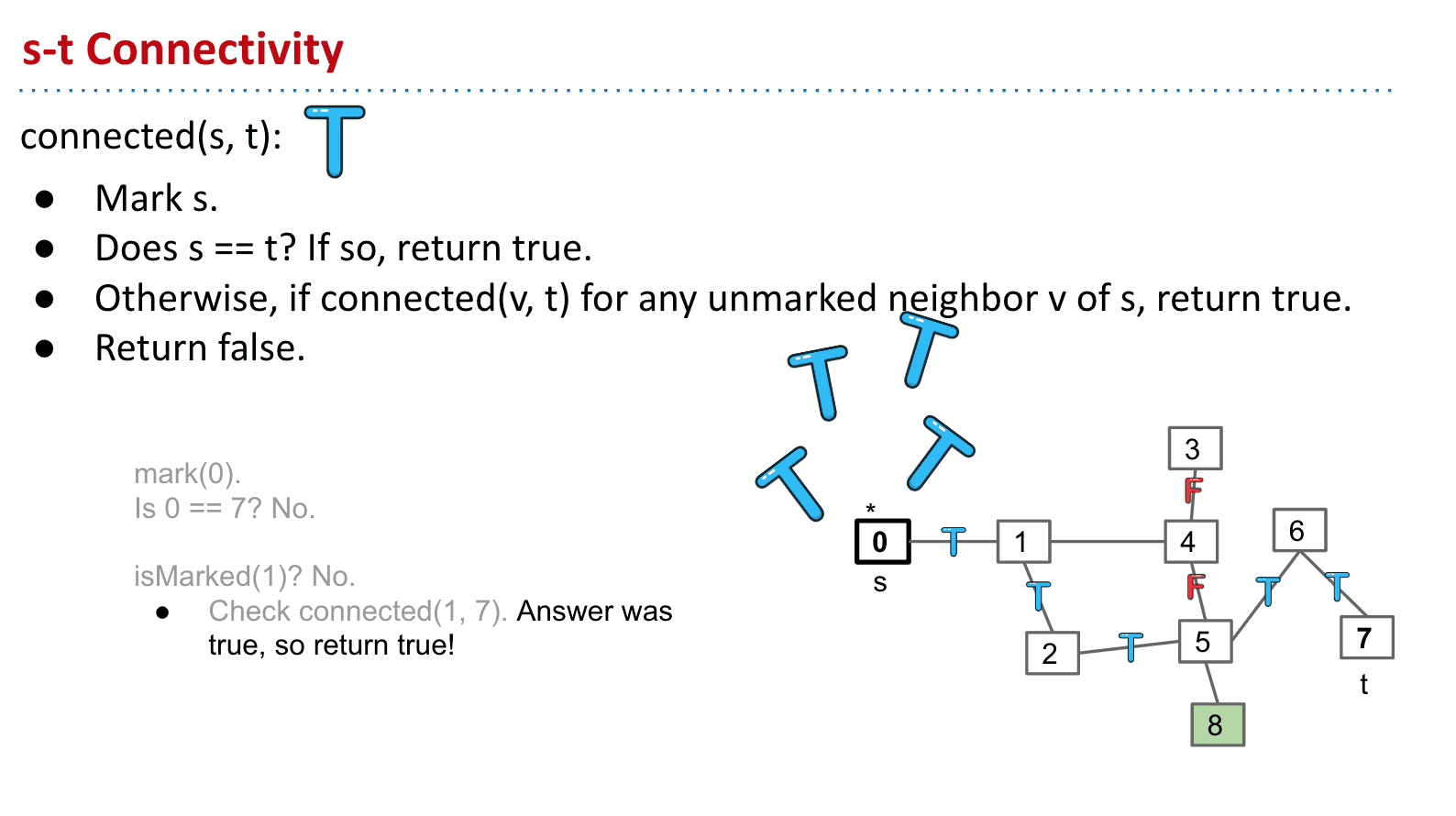
这样的算法其实就是深度优先遍历的一个子集
深度优先就是先尽可能的深入一个子节点再探索另一个子节点
- 使用DFS找到S到其他节点的路径 Demo演示
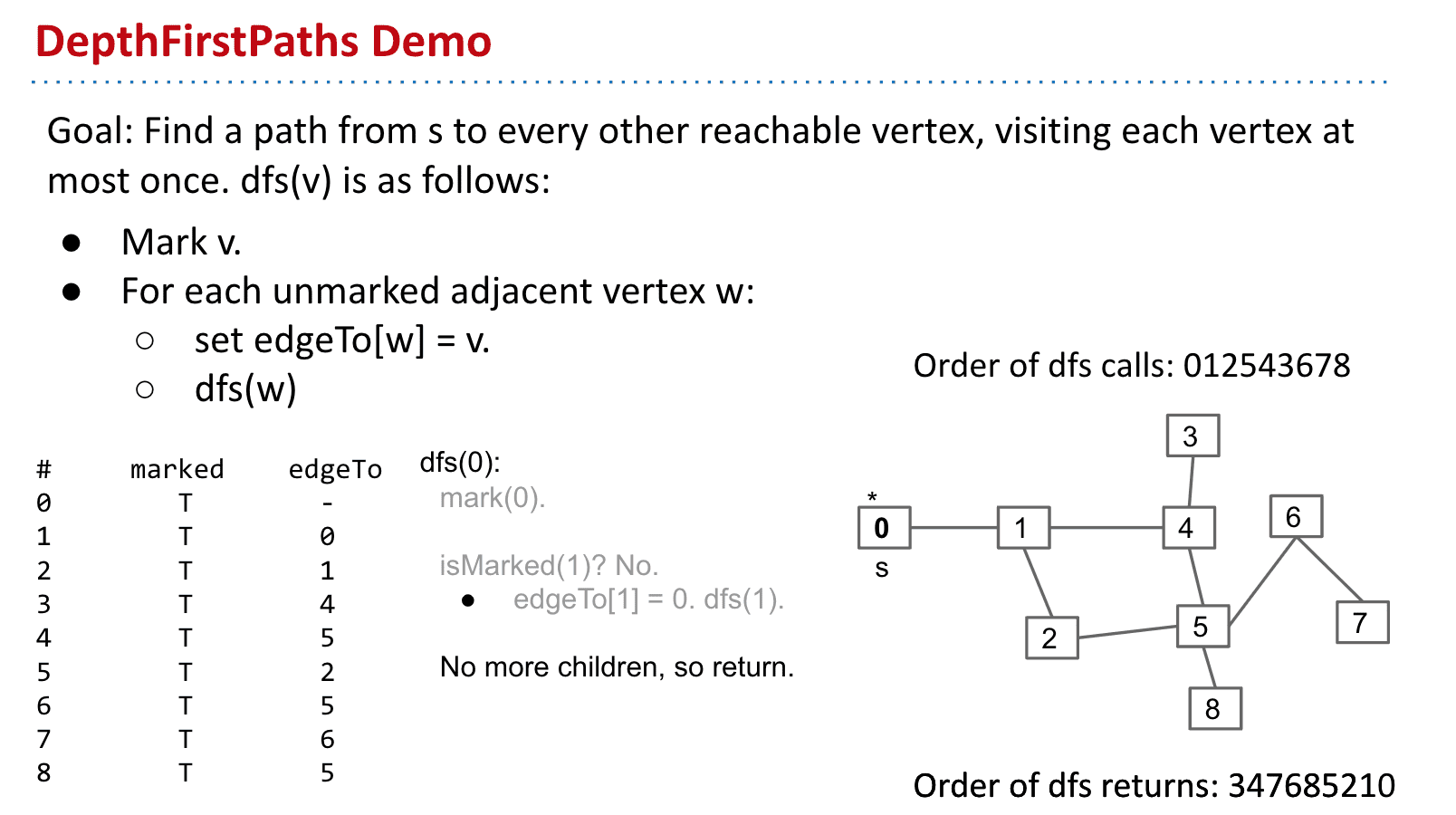
也被称为DFS Preorder
建立这个表需要从s点开始并选择一个点不断深入
访问的节点需要记录下是否被访问过,和访问它的那个节点
图的遍历
traversal可以解决大部分图的问题,通过在图(或树)的遍历过程中执行actions / setting实例变量,你可以解决像s-t Connectivity或path finding这样的问题。
-
DFS Preorder
上面的DepthFirstPaths就是DFS Preorder,操作先于DFS

dfs call:012543678
-
DFS Postorder
操作后于DFS

dfs call: 347685210
-
BFS (广度优先搜索)
根据到s的距离来操作(会在下一节课讲到,也就是广度优先)

0 1 24 53 68 7
使用BFS找到顶点到每个节点的最短路径
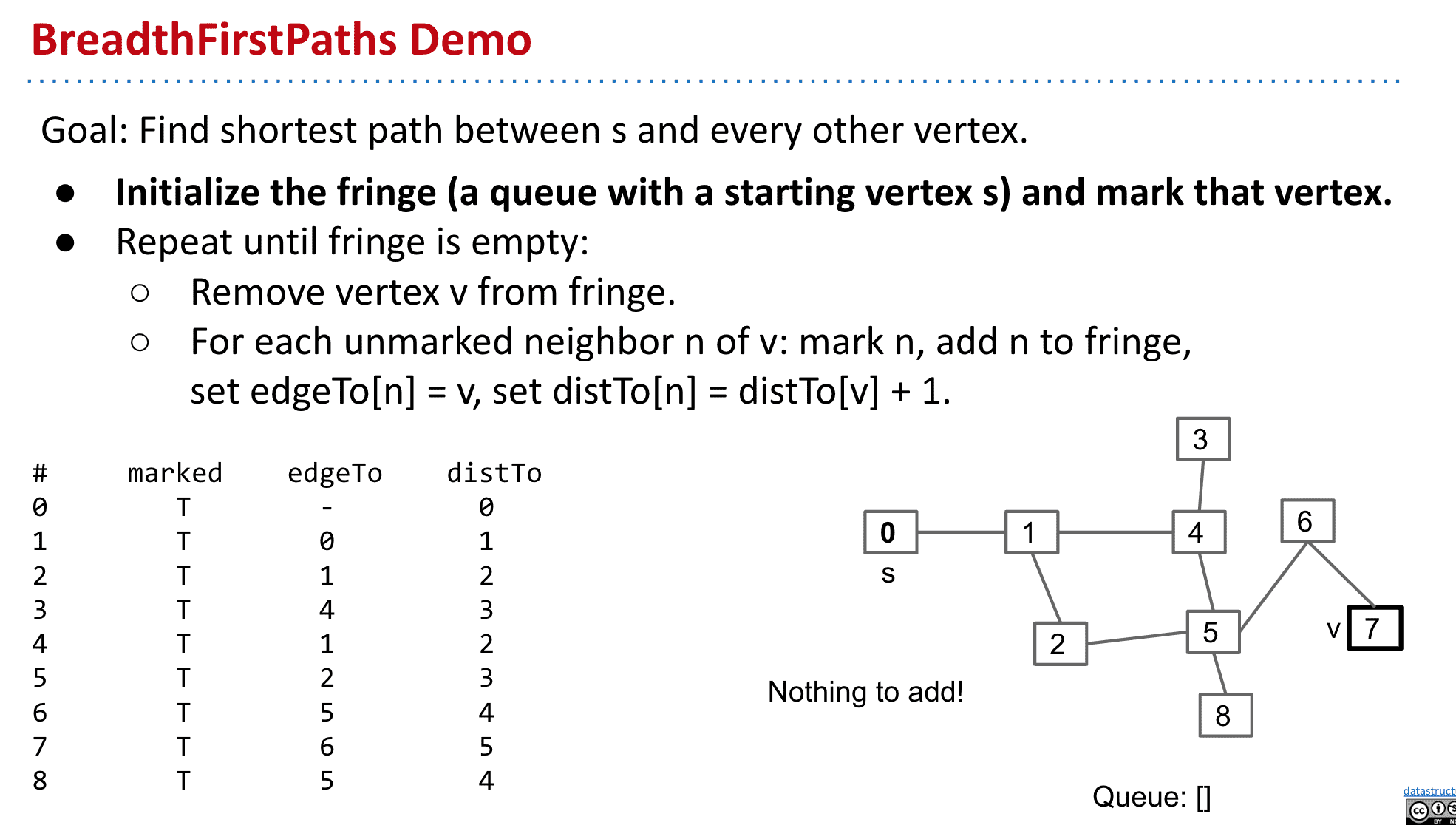
distTo是节点到s的距离,每一层+1
v不像dfs,bfs的顶点可以到处跳动
由于先进先出的属性,总是把一层探索完后再进入下一层
探索完成后就可以依靠distTo马上知道一个节点到s的距离了
BFS还可以应用在如寻找两个演员之间的最短电影关联的网站数据结构
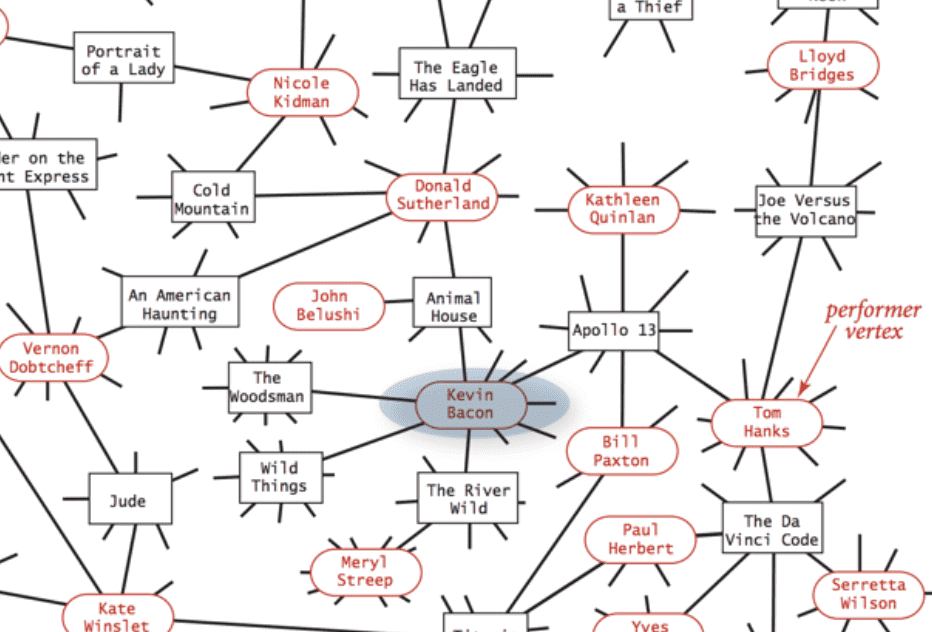
图遍历和树遍历的一个大区别就是图遍历的顺序可能不是唯一的,比如上图1之后可以去4也可以去2
Graph API

实现用BFS/DFS实现图需要的东西
一般情况会给节点加上label而不是实际的值,可以通过map来对应
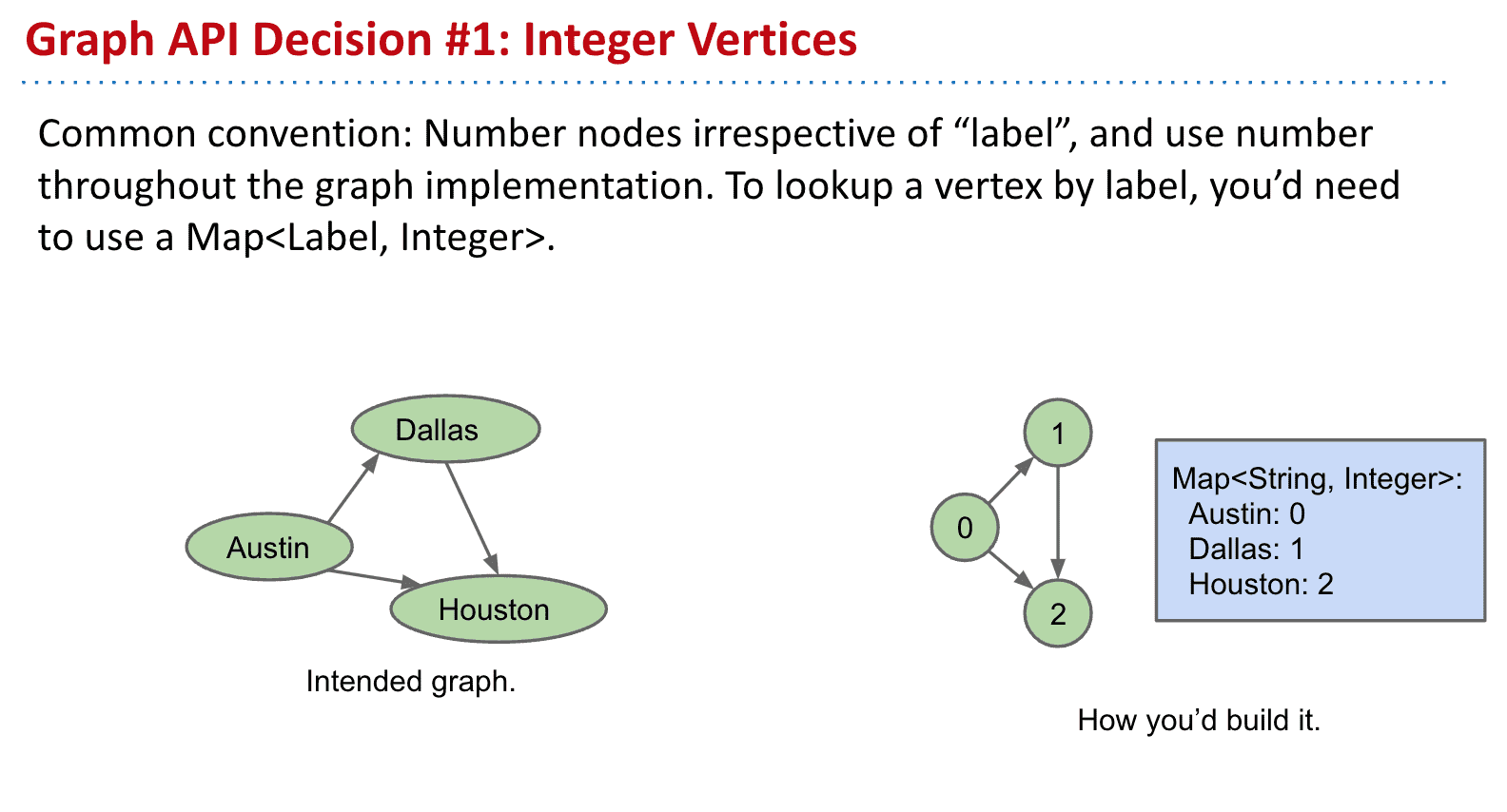

普林斯顿教材的图API
注意degree就是edges的意思也就是连接线

打印整个图的code
使用哪种数据结构实现图(图的存储)
树:
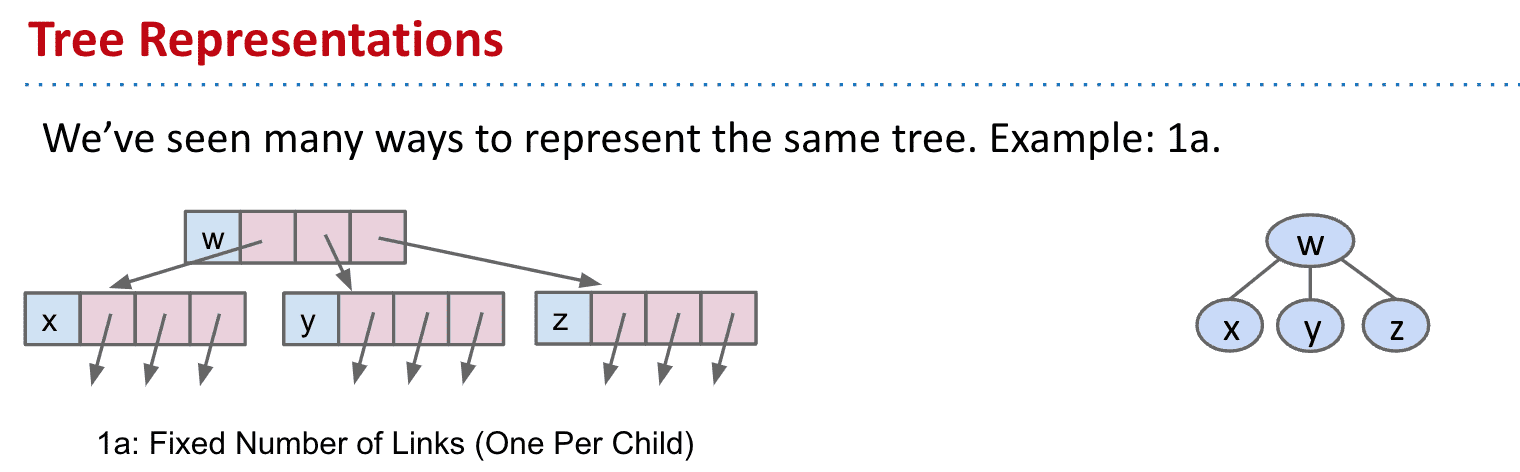
1.和一些树结构类似

2.和只存储key的结构类似⬇️,优点是使用较少的存储和快速,但只能用在完整的tree上
3.由于这个树很标准,可以只存储key不存储父节点
矩阵:
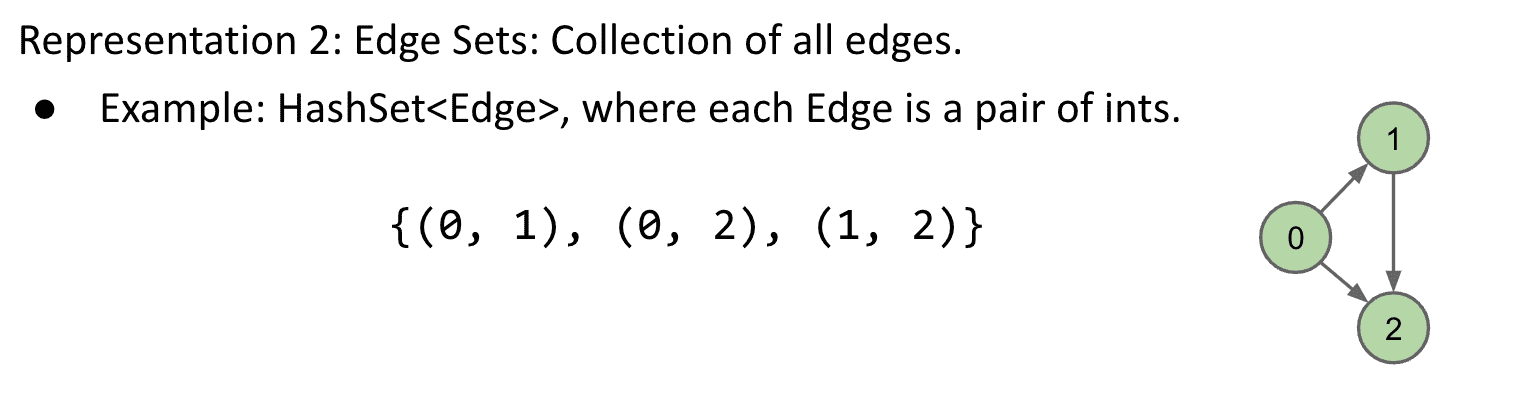
4.存储连接的集合

之前学过两种找到路径的方法,DFS不适用于瘦长的图,而BFS不适合饱满的图
但BFS有个好处就是可以找到S点到任意点的最短路径
但是在现实中,比如地图APP如果使用这种策略的话就会出问题,因为不是每个点之间的路径都是相同长的
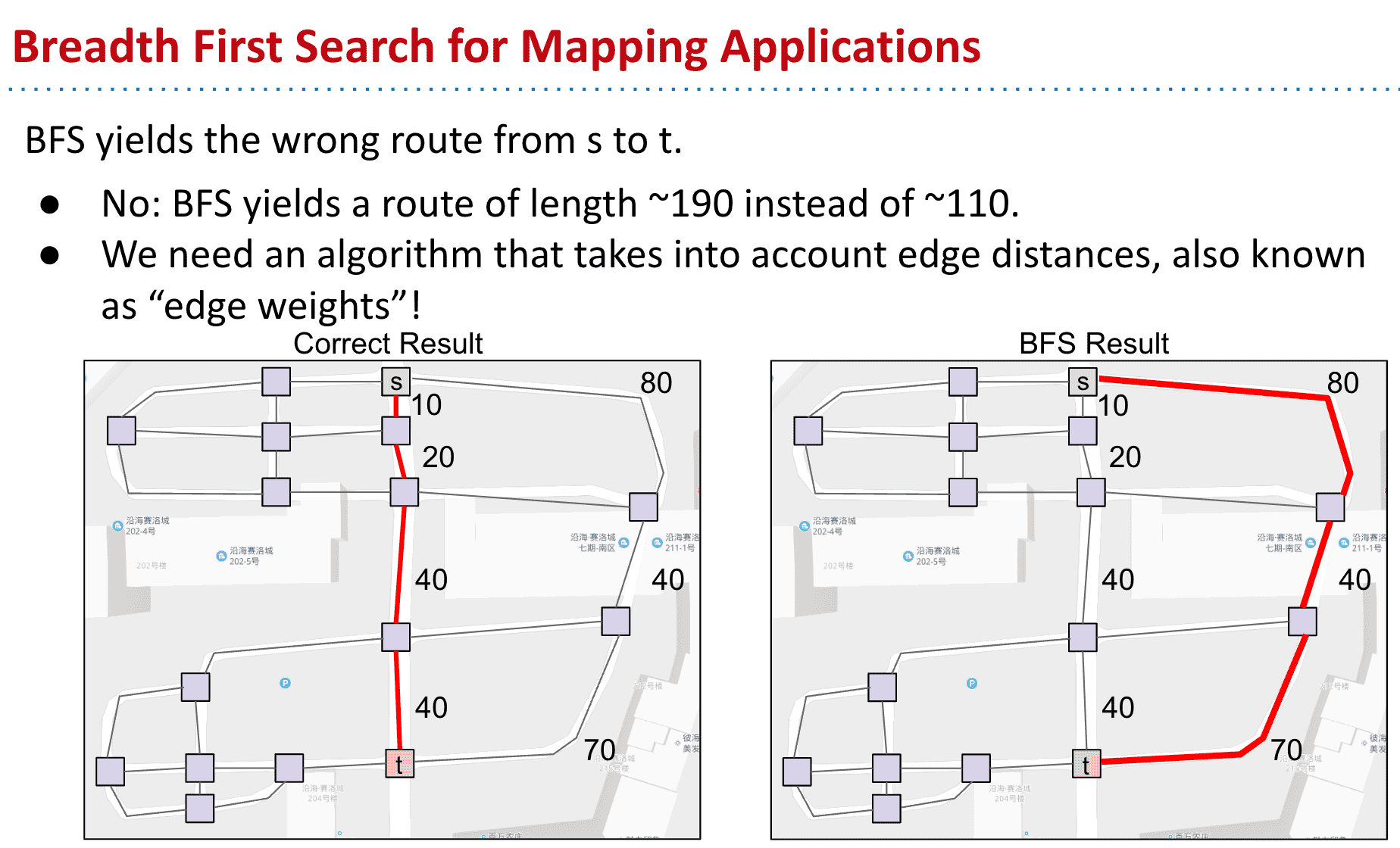
最短的路径却有更多edge所以使用BFS会选择edge更少的更长的路径
戴克斯特拉算法 (Dijkstra's algorithm)
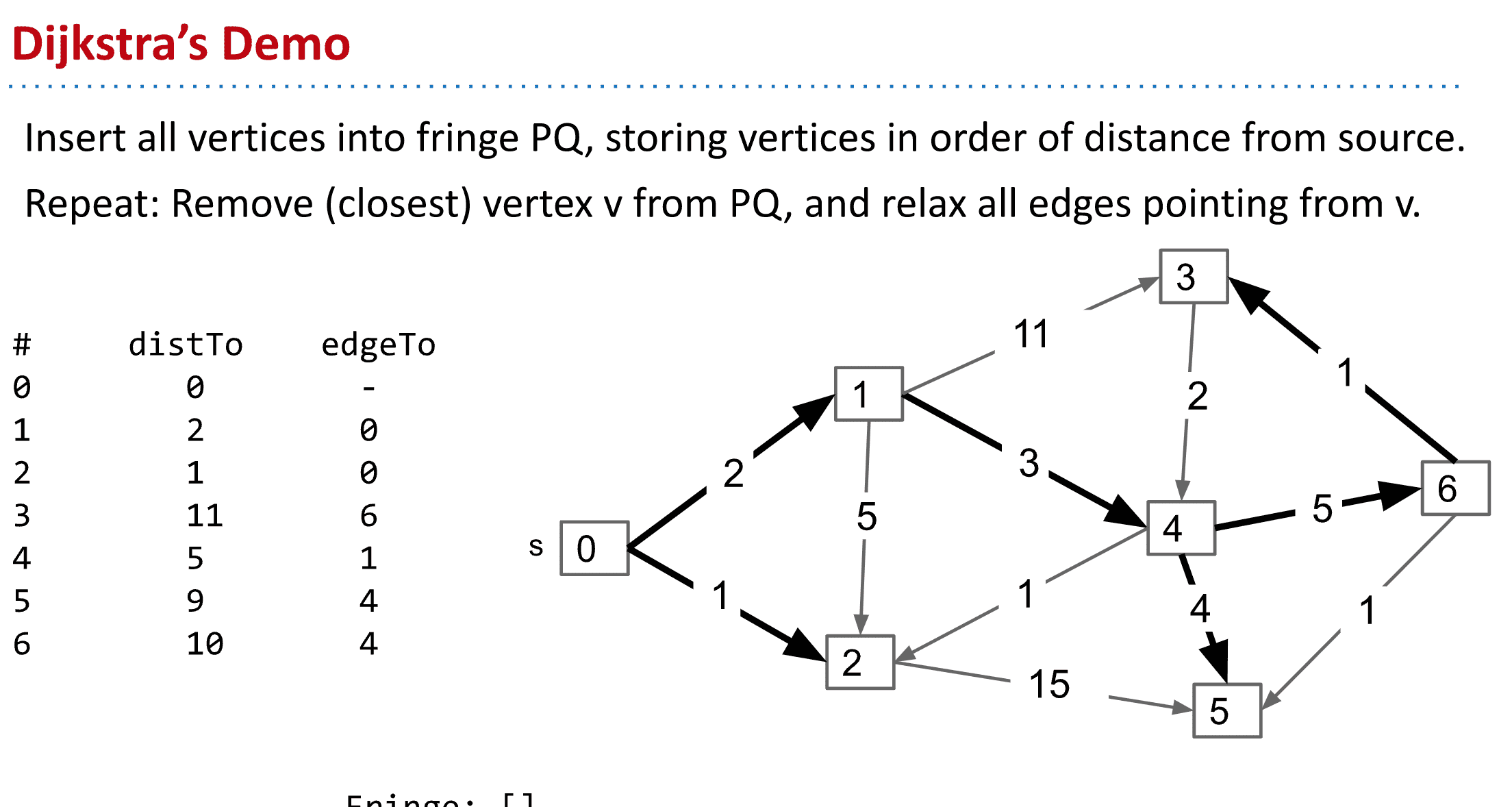
要点:不断更新S到顶点的最小距离,选择路径更短(priority queue可以帮助)的顶点为下一个探索的顶点,最终形成一个最短路径的tree
从S到各点的最短路径最终就像是tree一样
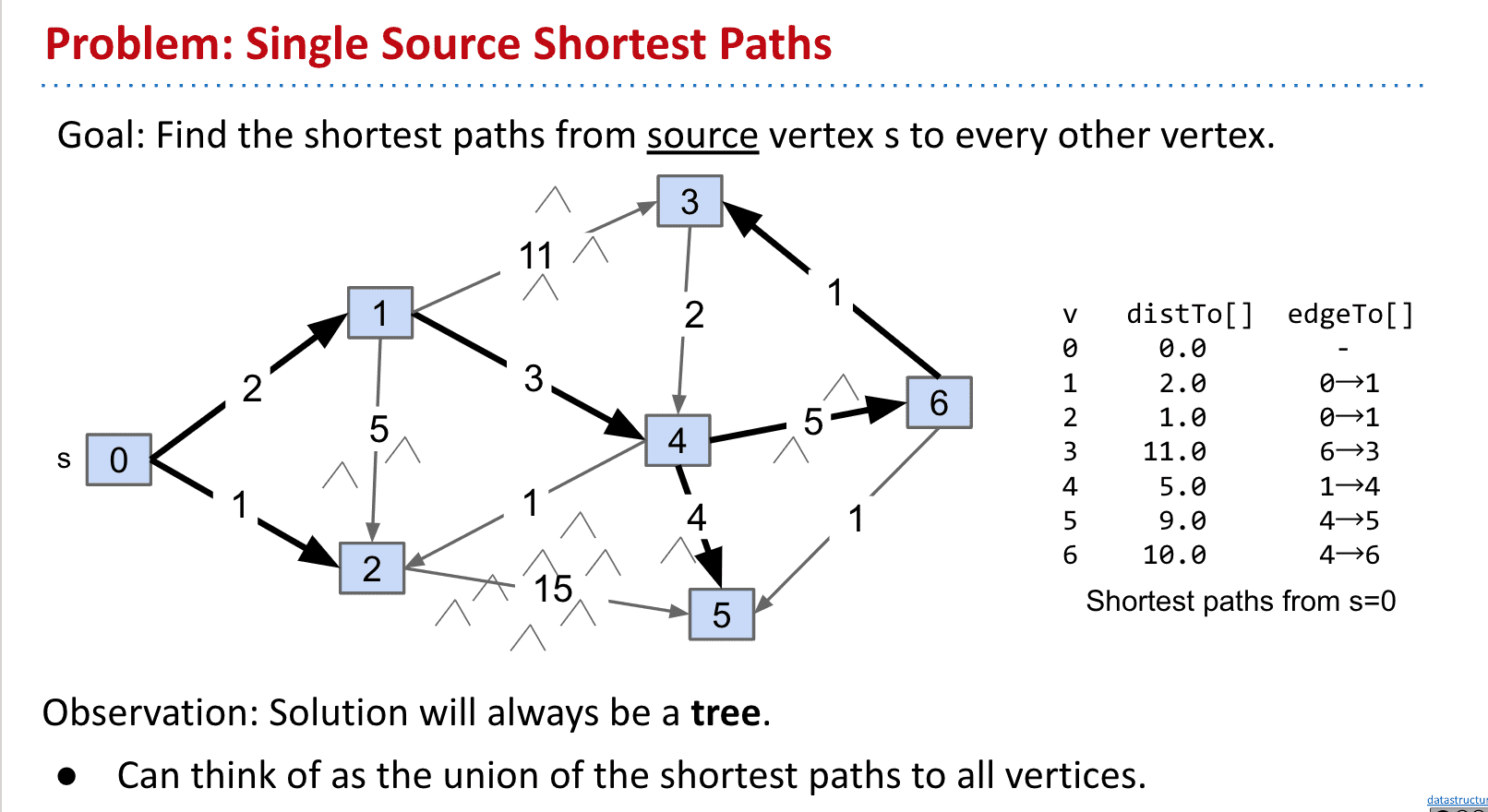
而我们可以靠给S到节点标记距离来找到最短路径,最开始默认所有的S到节点的距离为♾️
到实际访问时再标上真实的距离,如果有更短的距离就进行覆盖这样就得到了Dijkstra's algorithm
Dijkstra’s Algorithm Demo Link
另外访问下一个顶点(节点)时总是选择最小的路径来继续
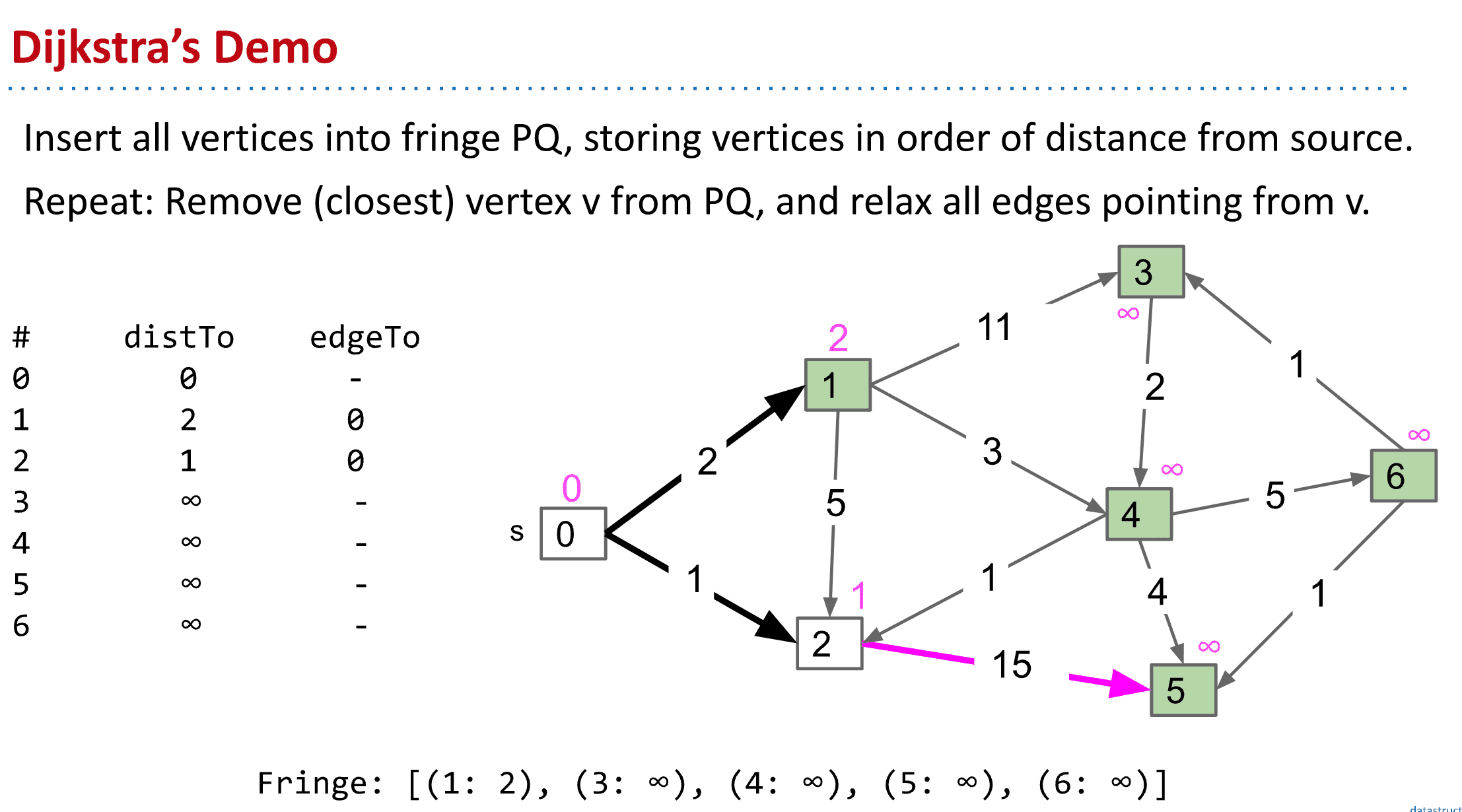
通常使用PQ来保证路径
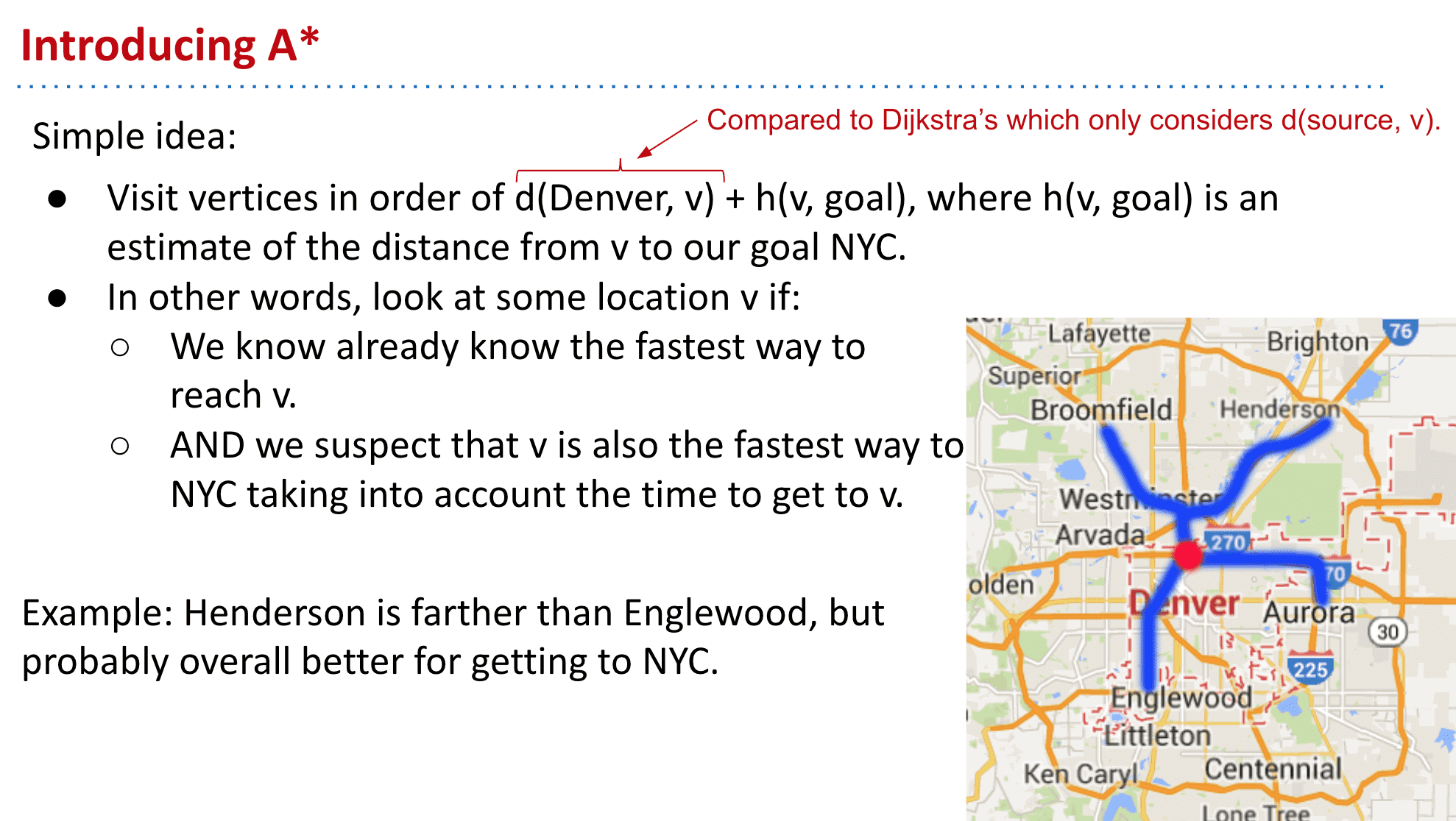
A*
Dijkstra有个缺点就是会探索所有顶点,但我们从A地到B地并不需要探索完A周围的所有顶点,于是就引入了一个估计值,也就是说我们会尽量探索靠近B点方向的节点(也就是说Dijkstra探索下一个顶点的依据是最短距离,而A*探索的下一个顶点是我们估计与目标顶点距离更近的顶点)
A*算法根据f值f=g+h来构建优先级队列(D只有g),其中g是起始点与顶点的距离,h是顶点到结束点的距离。D算法是根据g值来构建
给定一个无向图,确定它是否包含任何循环
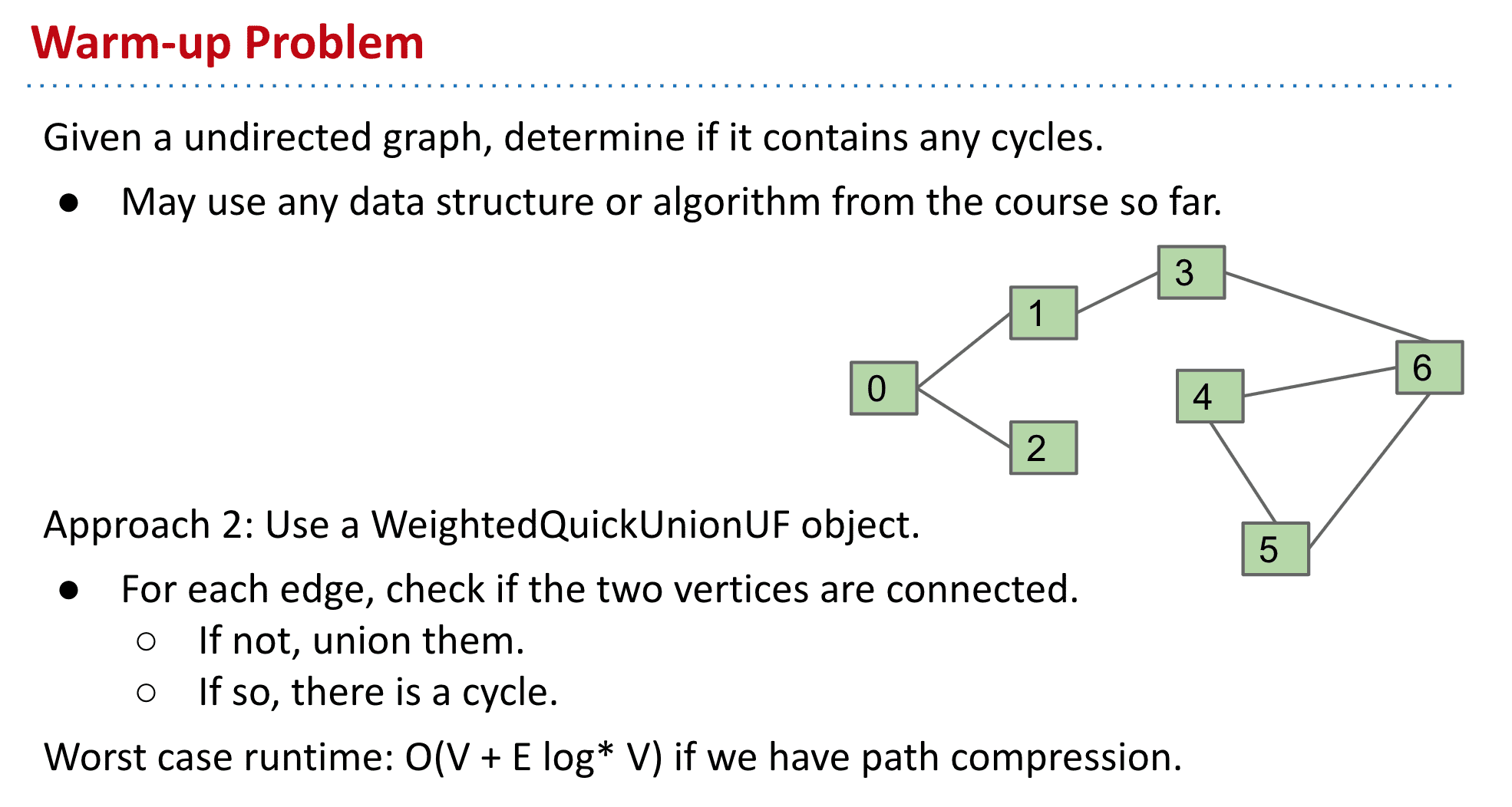
解决方法
1:使用DFS只要再次遇到已经标记过的顶点就说明有循环♻️(注意要除去到这个顶点的顶点)
2:使用WeightedQuickUnionUF,大概就是没连接的点union,有连接的点之间比如4,5 4,6 5,6都union了说明是循环(这个我也不太懂)
生成树 Spanning Trees
是无向图的一个子图,无向图 G 的生成树是具有G 的全部顶点,但边数最少的连通子图
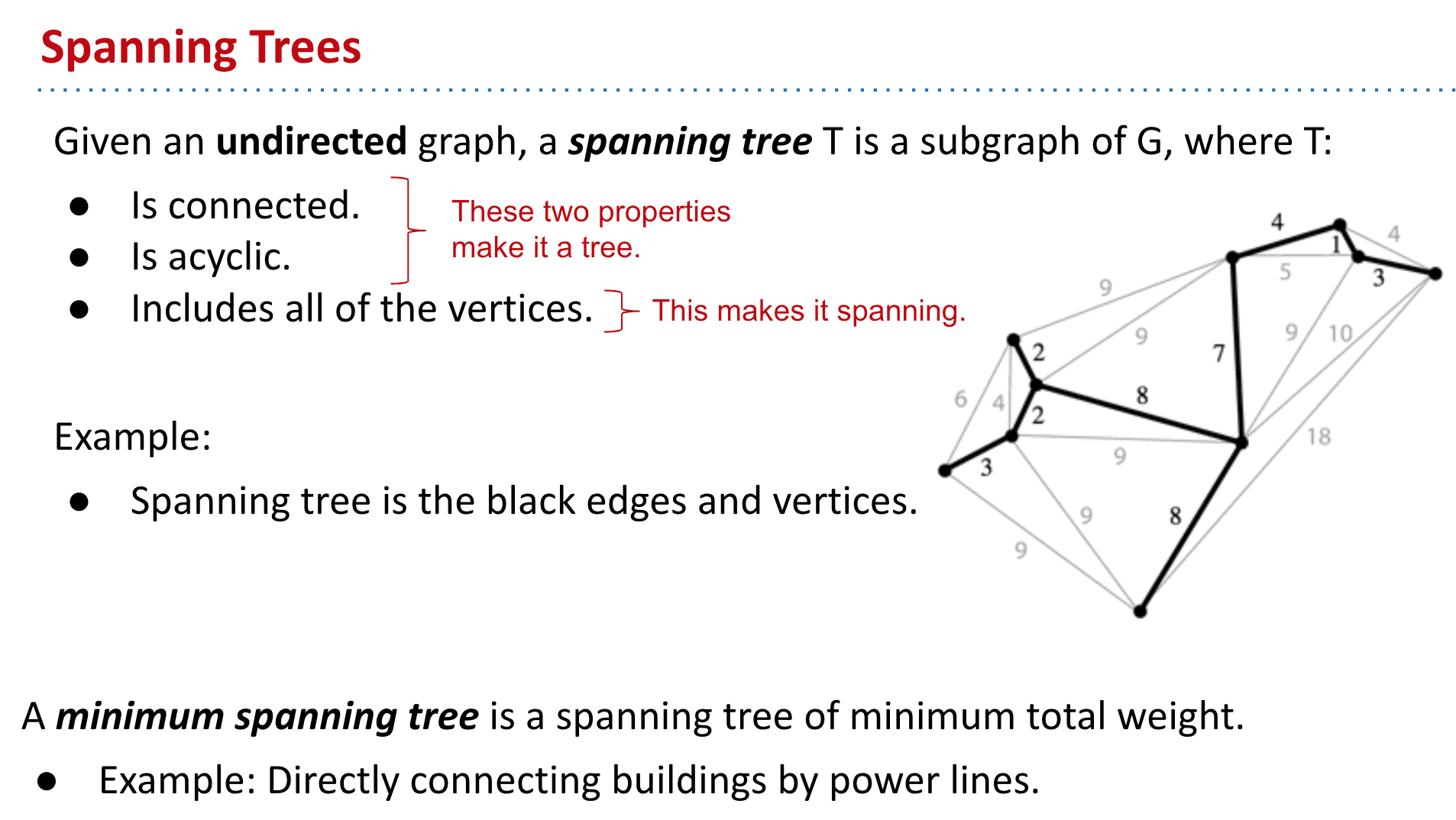
连接、不循环→tree、包含所有顶点→spanning
MST 最小生成树 (Minimum spanning tree)
就是无向图的生成树里面权值最小的生成树
MST的现实应用:比如不同城镇间建立线路最短的电网
MST vs. SPT
MST是没有S(source)的,它的目标是连接所有顶点并且路径最短,而SPT的目标是找到S到所有节点最短的路径
在某些情况下他们可能长得一样
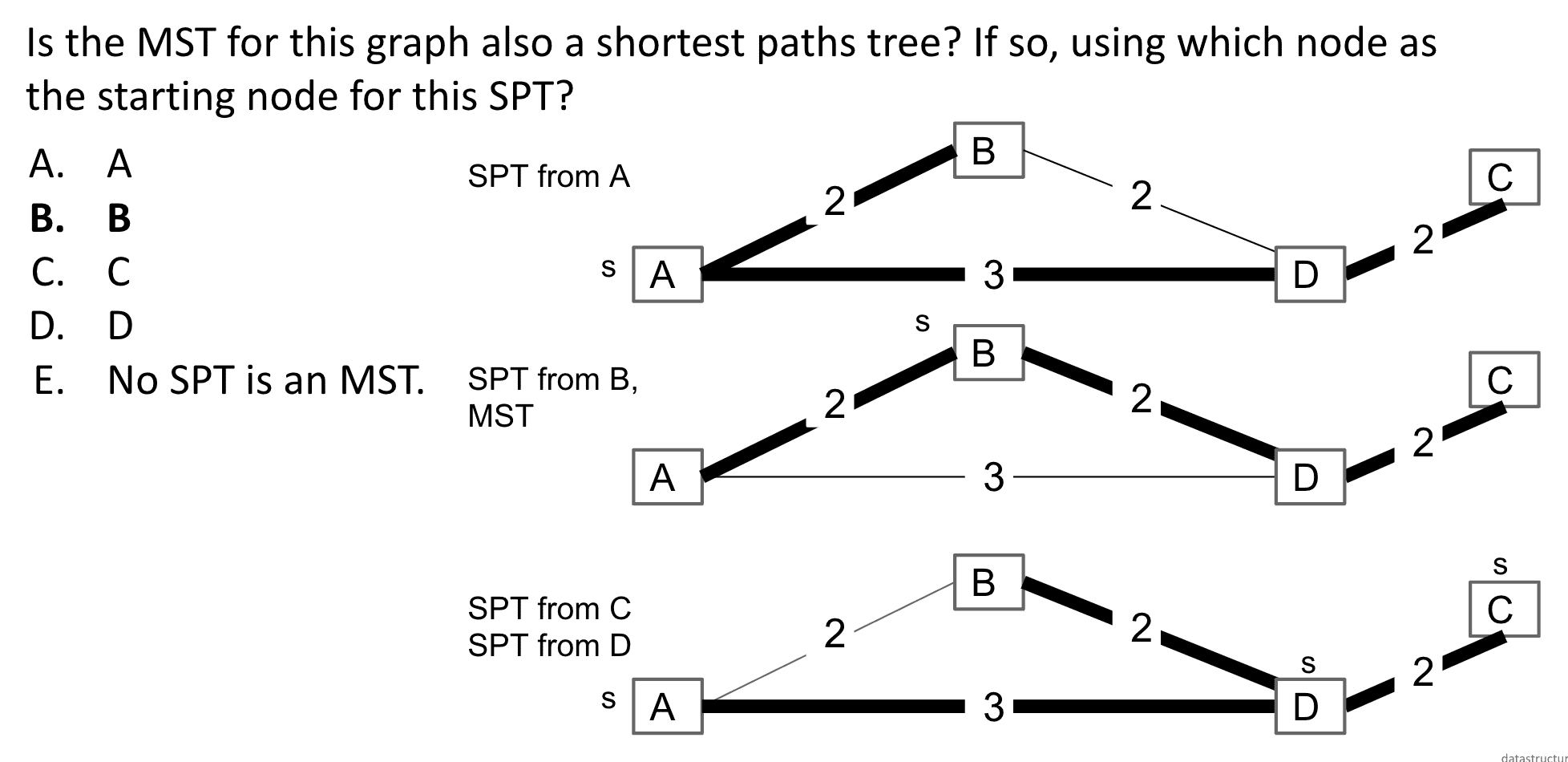
B点为S的SPT与MST一样
如图红线就是横切边
证明:如图我们找到了最短的横切边
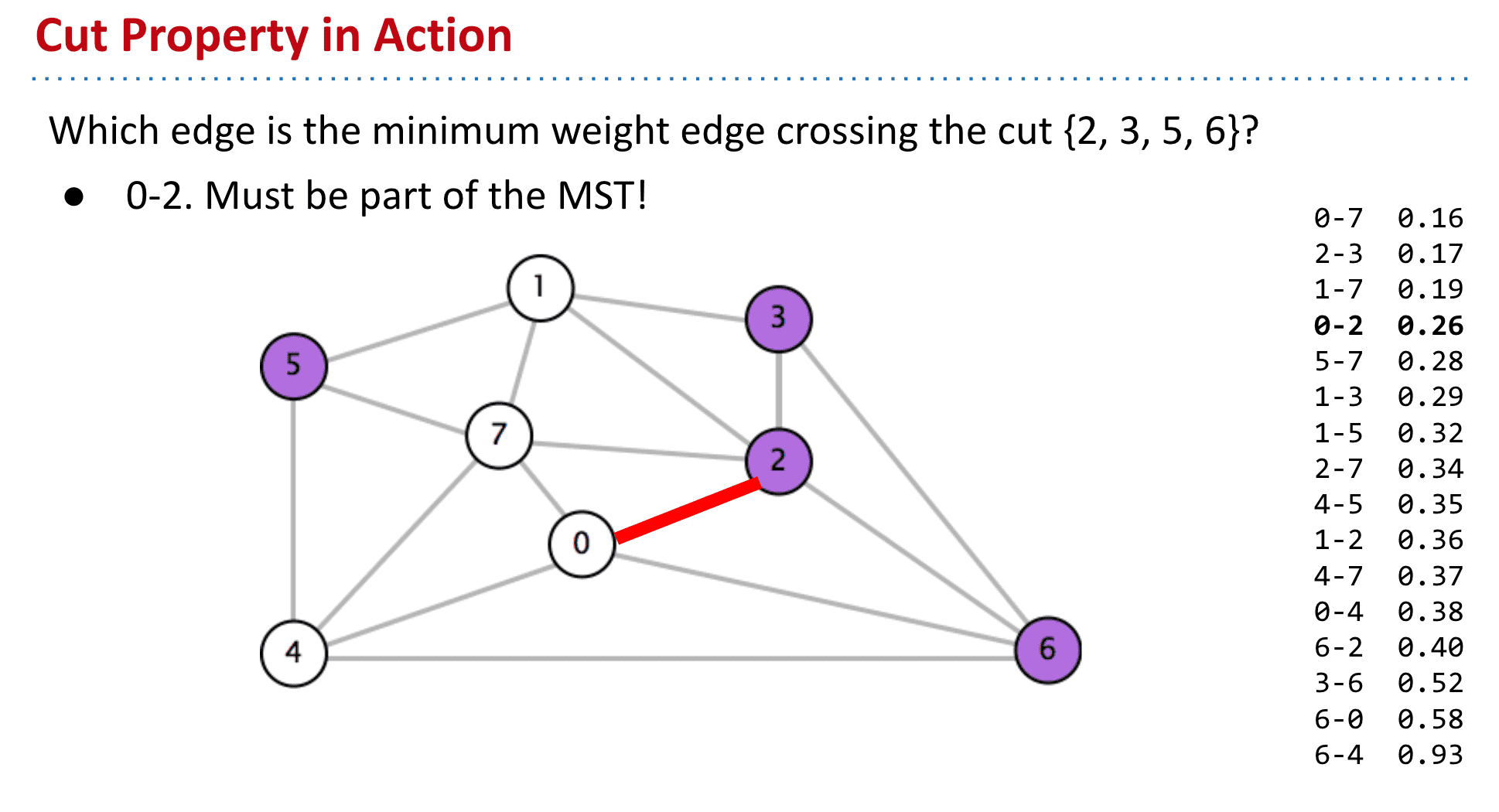
如果e不是MST的一部分,把它加入MST就会形成循环
这时候减去f得到的MST,必定是路径更短的MST
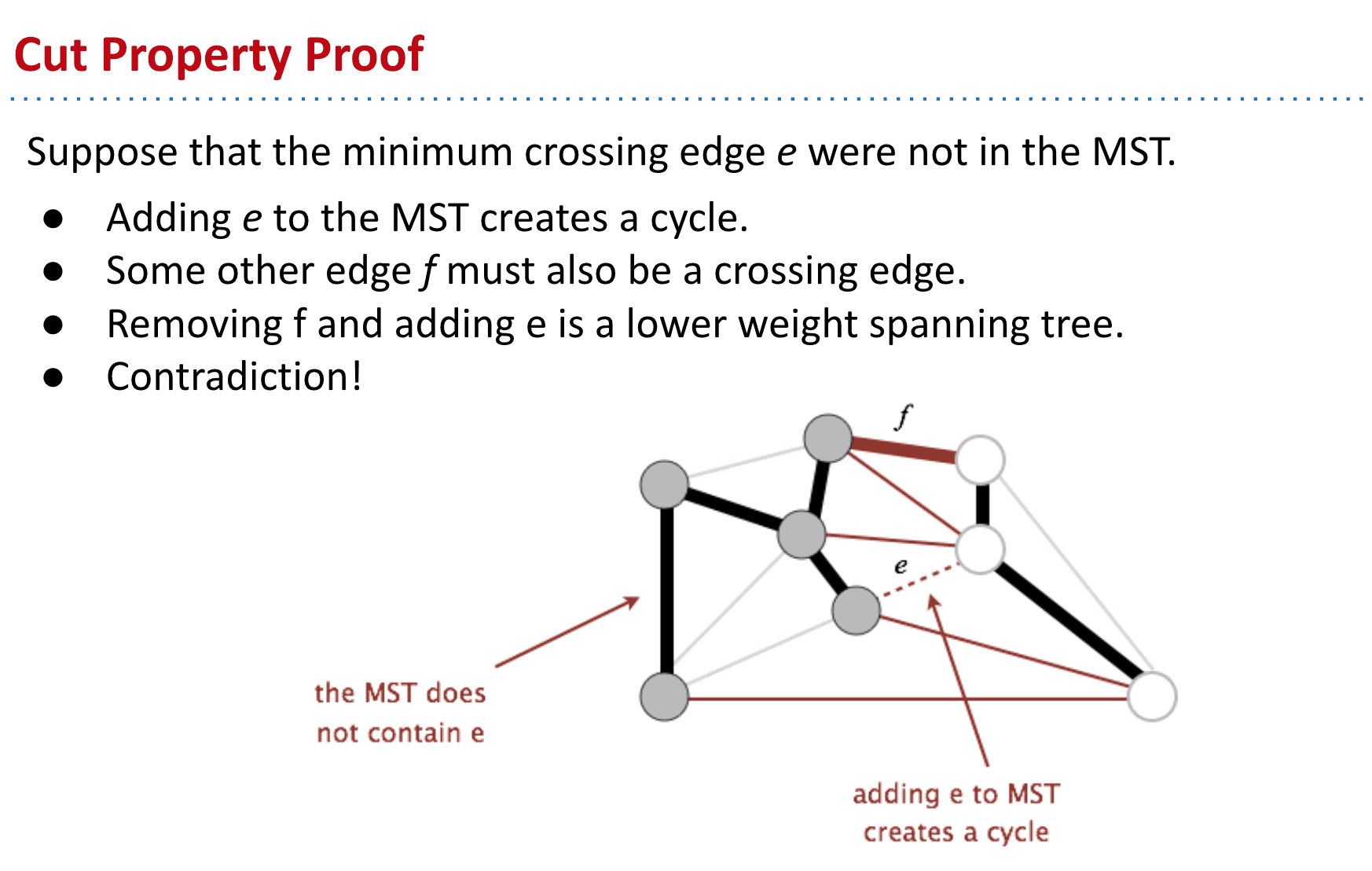
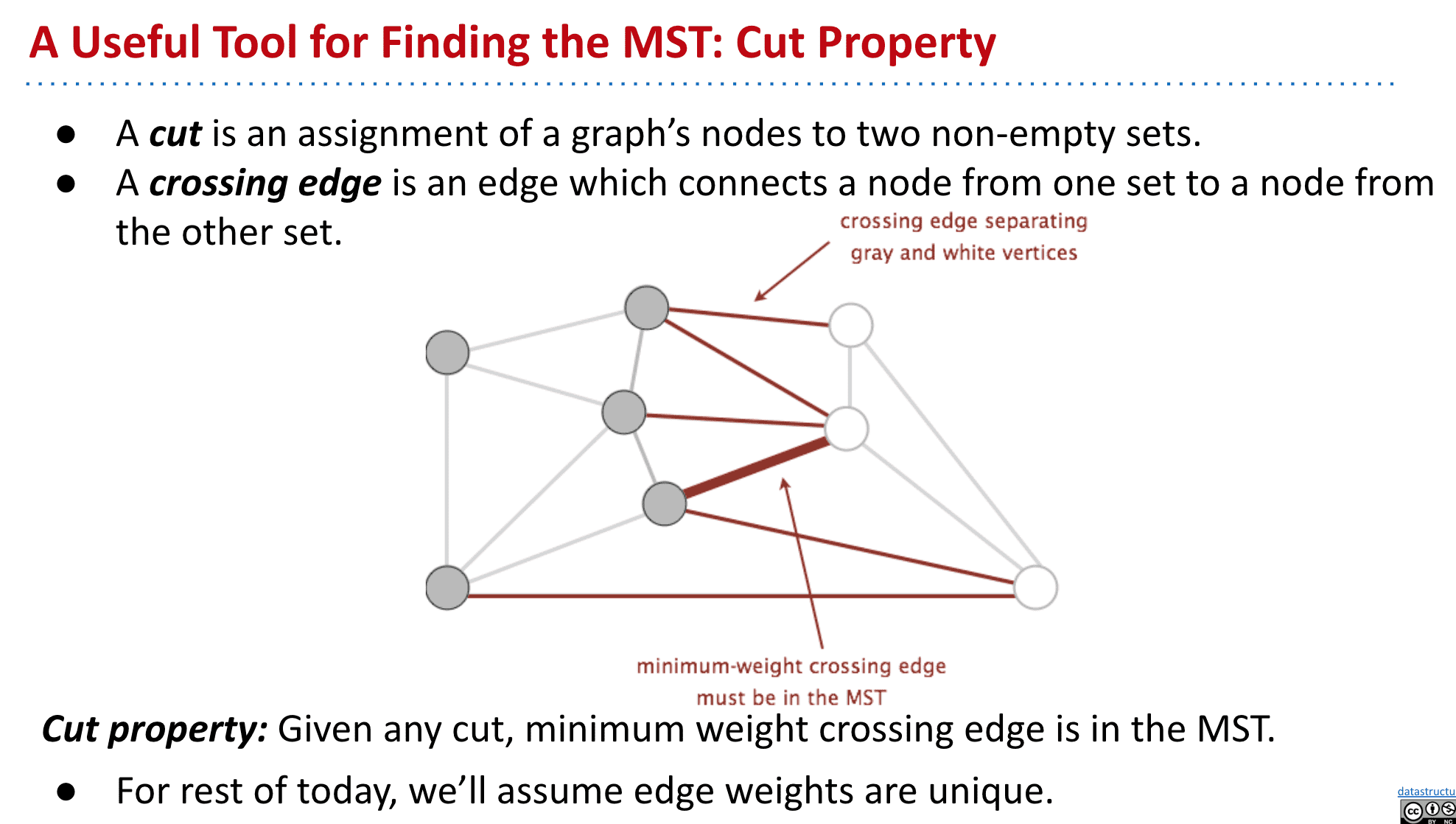
使用切分定理来找到MST
我们可以一直生成不同的set(把顶点们随机分为两部分),然后其中最小的edge就加入MST,最终就能得到完整MST了

但是又有一个新问题:“Random isn’t a very good idea.”也就是依靠随机分set并不是很可靠也就引入了使用切分定理的下一个算法
普里姆算法 Prim's algorithm
随便选择一个顶点开始,然后每次都选择最小的边加入MST,直到加入了V-1条边,就得到了MST
其实就是切分定理的一个应用,相当于把已经选择过的顶点和余下部分分为了两个set,再找到最短的横切边加入MST
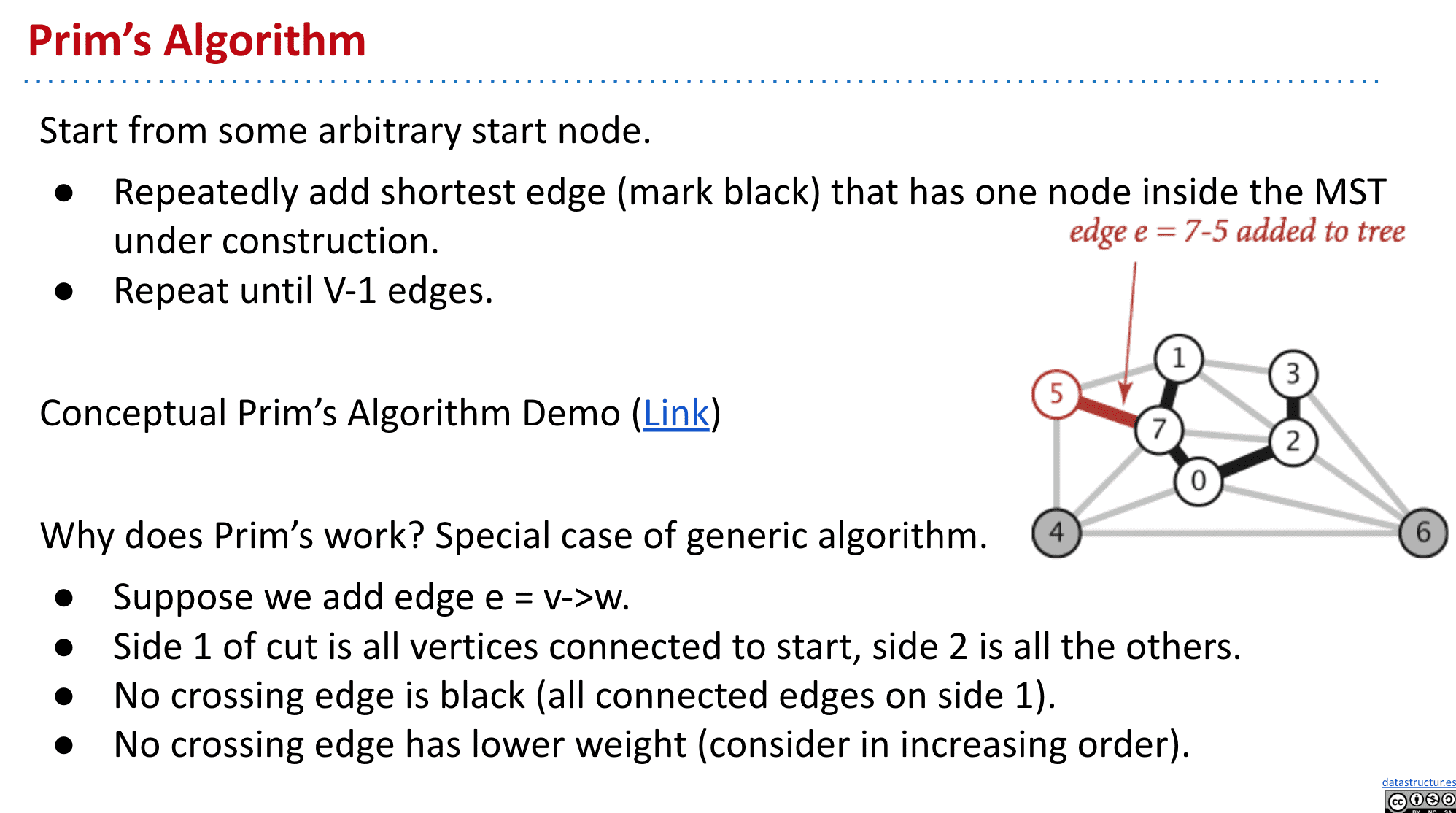
不过这种Prim's algorithm有个缺点就是可能最后有太多需要考虑的边了,效率不高
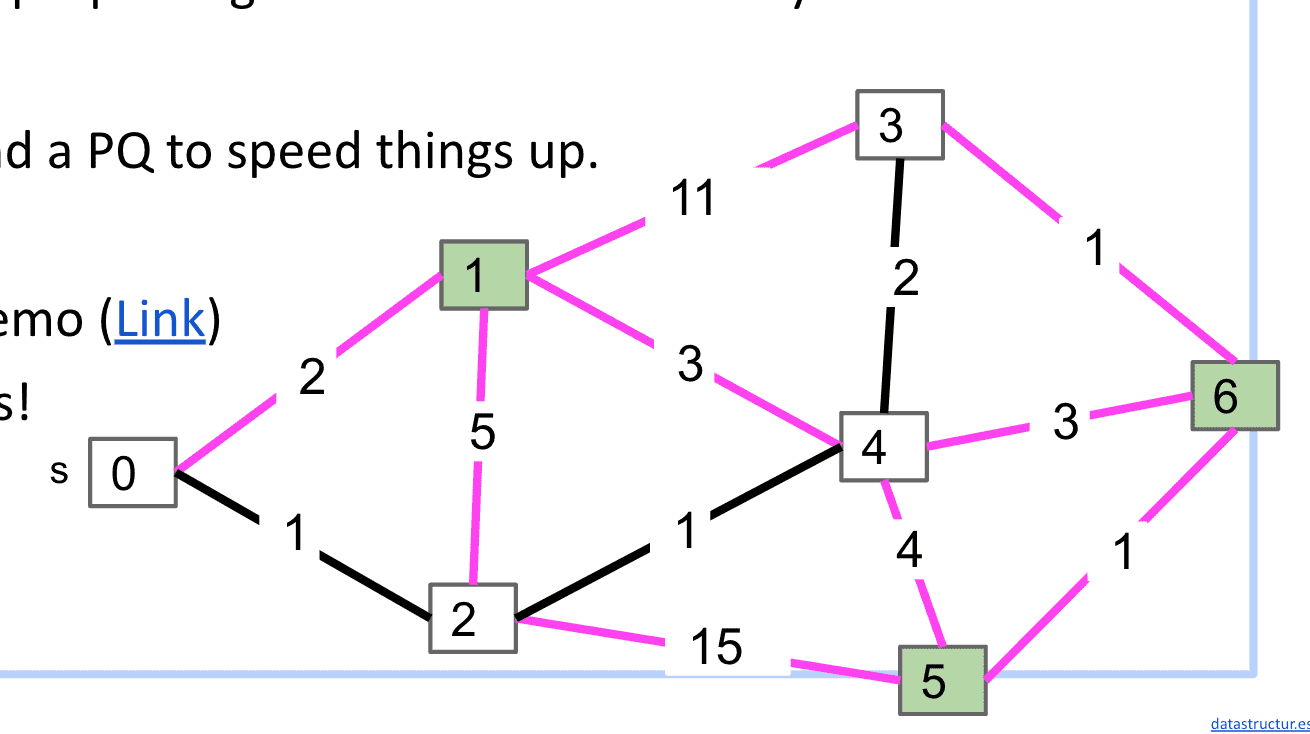
所以我们可以学习Dijkstra的想法,把顶点们以到S距离放入PQ,并且不断移除确认了最短边的节点,这样就不用考虑所有紫线了(不是很懂,建议看演示理解)
Prim’s vs. Dijkstra’s
这两种算法基本相同,只是关注的东西不一样一个在乎相邻未加入顶点edge的PQ里的最短,一个在乎S到顶点的距离最短(也就是他们选择下一个顶点的逻辑不一样)
总的来说Prim关注集合(Set)和集合,而Dijkstra关注一个顶点到其他所有顶点,除此之外思想是差不多的

但是Prim的实现还是比较复杂的,所以有了更简单而且也不用随机选择相同权值的新算法——克鲁斯克尔算法 (Kruskal's algorithm)
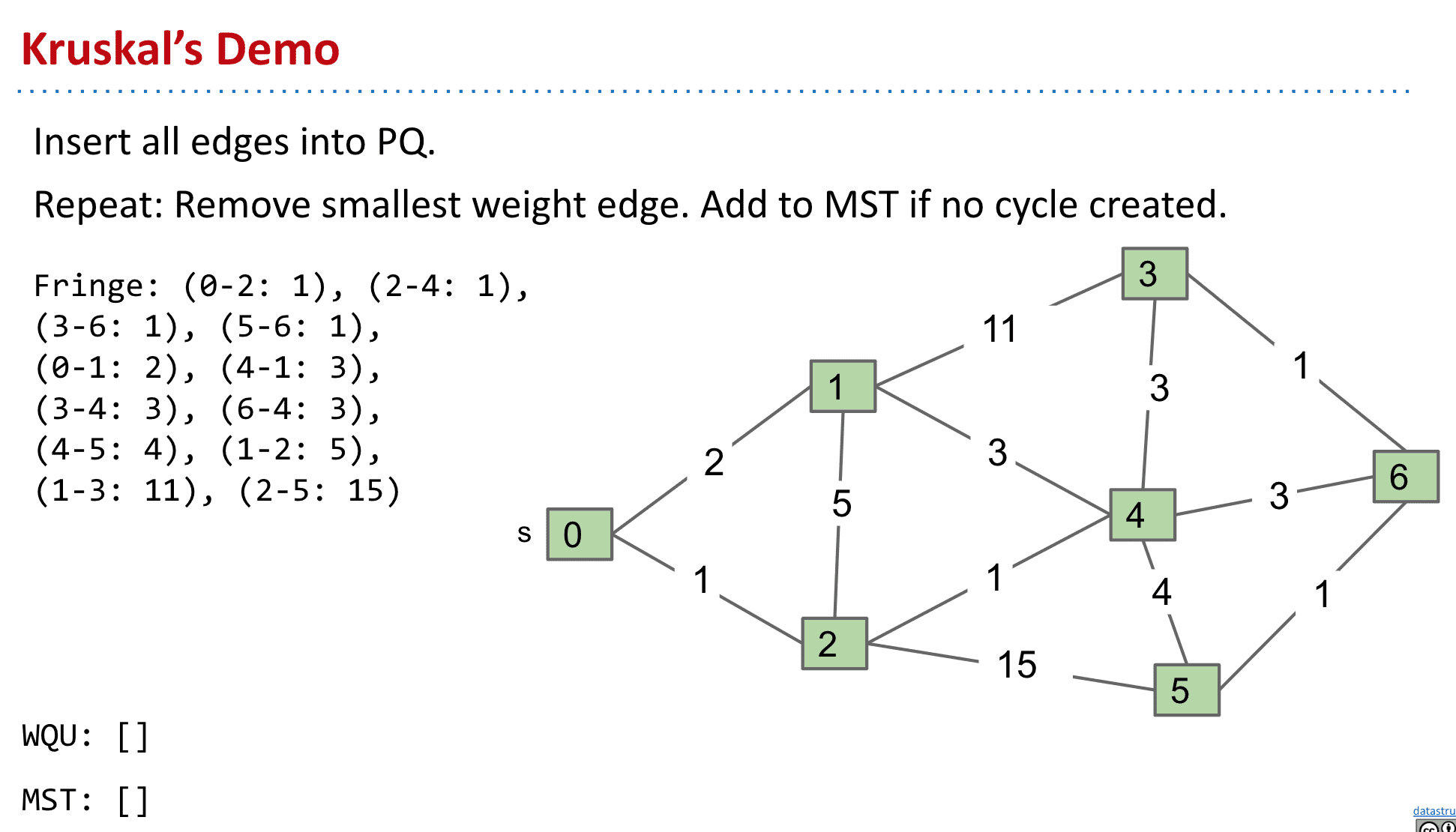
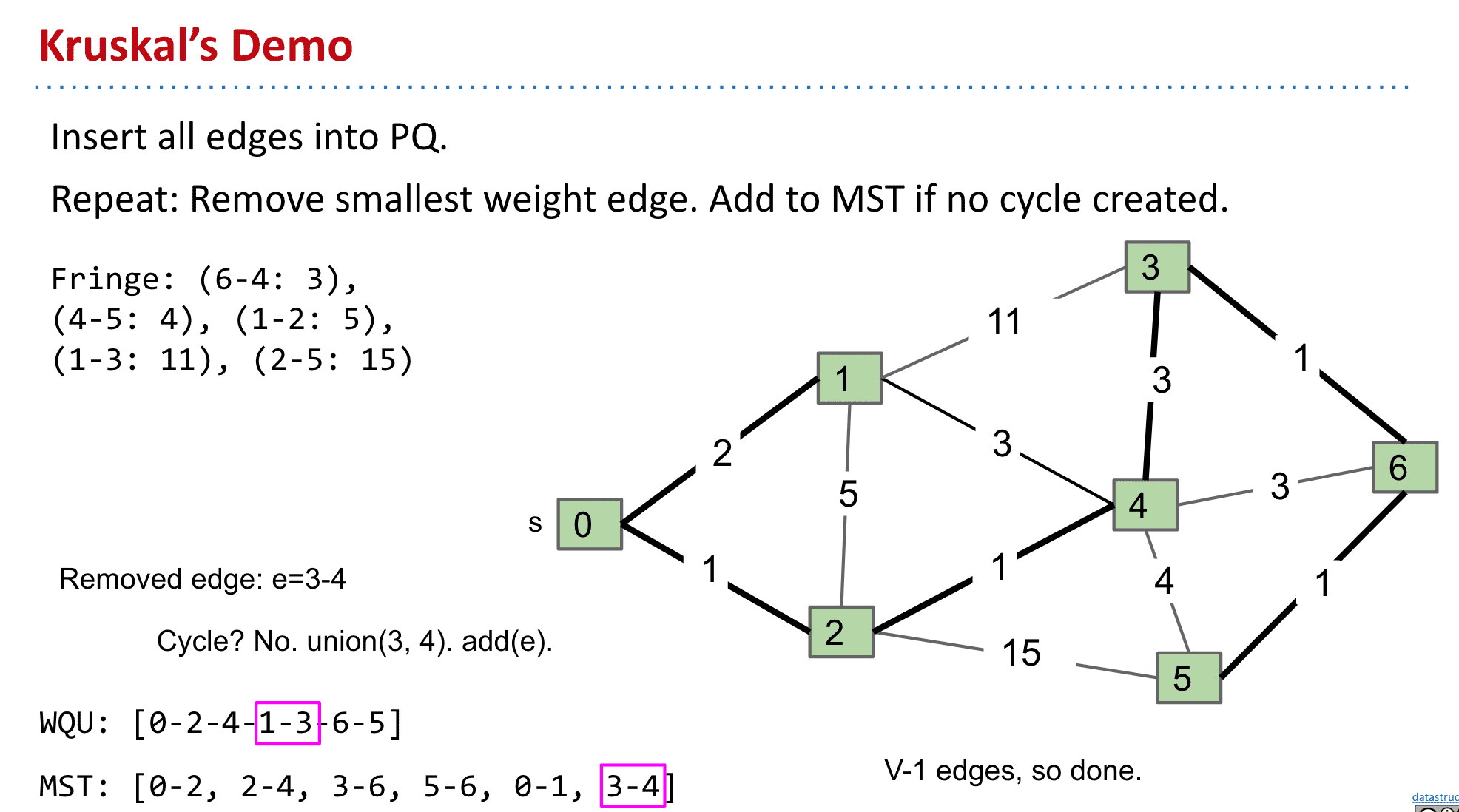
克鲁斯克尔算法 Kruskal's algorithm
将edge按权值由小到大排列,然后只要新加入MST的edge不构成循环就加入.最终V-1是就完成了MST了(和Prim不一样,构建时的MST不一定都相连)
同样也贯彻了Cut Property,可以把已经加入MST的点和未加入的想象为2个set,总之既然MST包含全部顶点,那么不构成循环的权值低的edge势必会被考虑

最短路径和各种MST算法总结,实际情况E和V的差别没多大,所以想用哪个算法都可以只是Dijkstra不适用于负的权值
tree的结构可以支持各种操作(一维)
假定有set:{1, 4, 5, 6, 9, 11, 14, 17, 20}
-
select(int i): 返回按从小到达排列的第i个最小的值
select(0): 1、select(3): 6 -
rank(T x): 返回 set中第几个的“rank” (与select相反).
rank(1): 0、 rank(6): 3 -
subSet(T from, T to):返回from到to之间的items(类似于子集)
subSet(4, 9): Returns {4, 5, 6, 9}、subSet(3, 12): Returns {4, 5, 6, 9, 11}、subSet(12, 13): Returns {} -
nearest(T x): 返回最接近x的值
nearest(6): Returns 6、nearest(8): Returns 9、nearest(10): Returns 9 or 11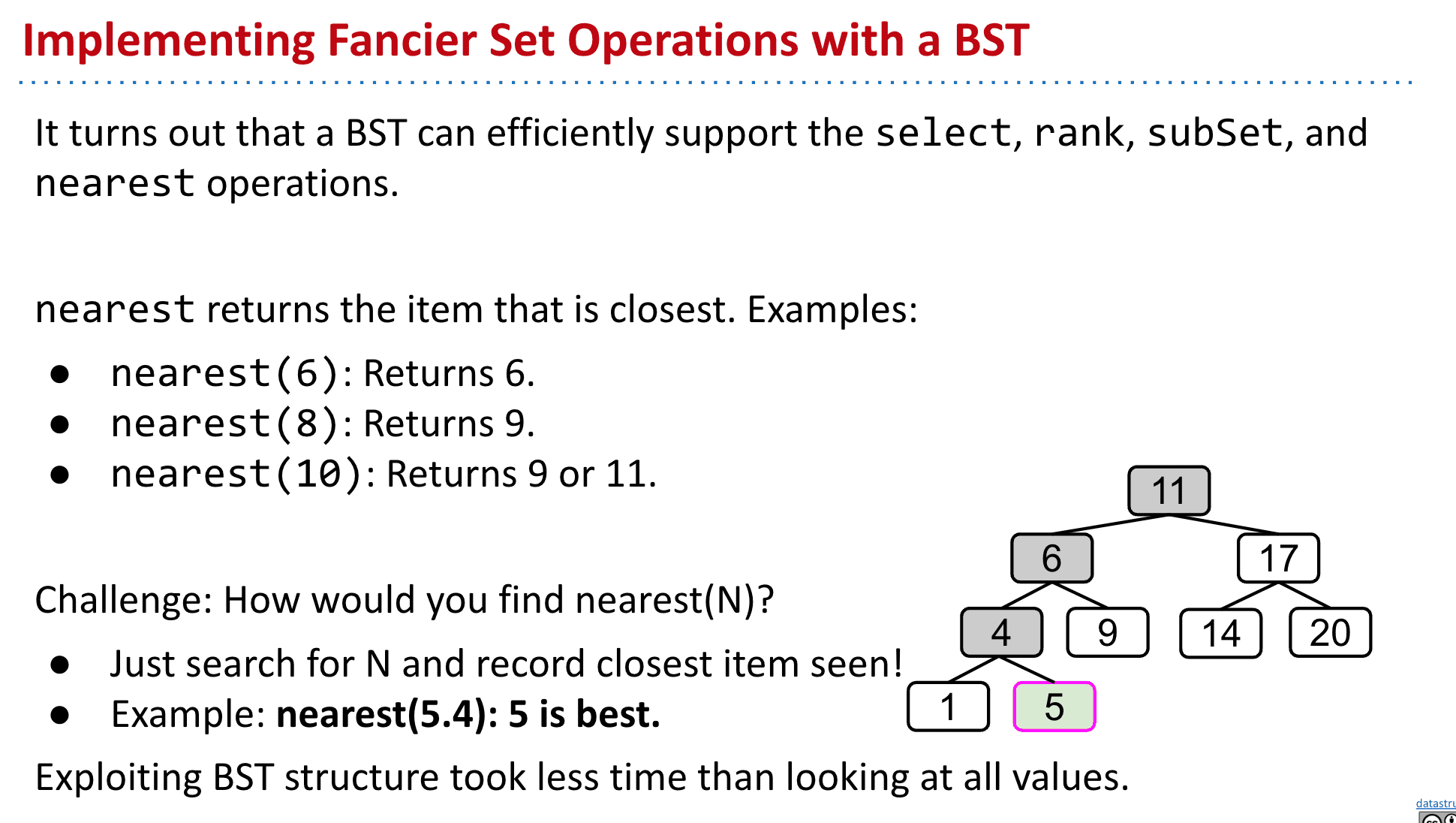
实现这个功能只需要search这个值并且不断更新并记录一个最靠近它的值就行了,其他功能的实现也与它很类似
以上这些都说了tree这个结构对各种操作都很有效率
但是我们这些都是一维的数据,而多维的tree和各种功能怎么设计就需要更进一步讨论了

多维数据不能使用BST
比如我们有一个有x,y信息的数据,只通过X或者Y得到的BST很可能不一样,想要在以Y生成的tree里找到X小于某个值的顶点的话必须遍历全部顶点
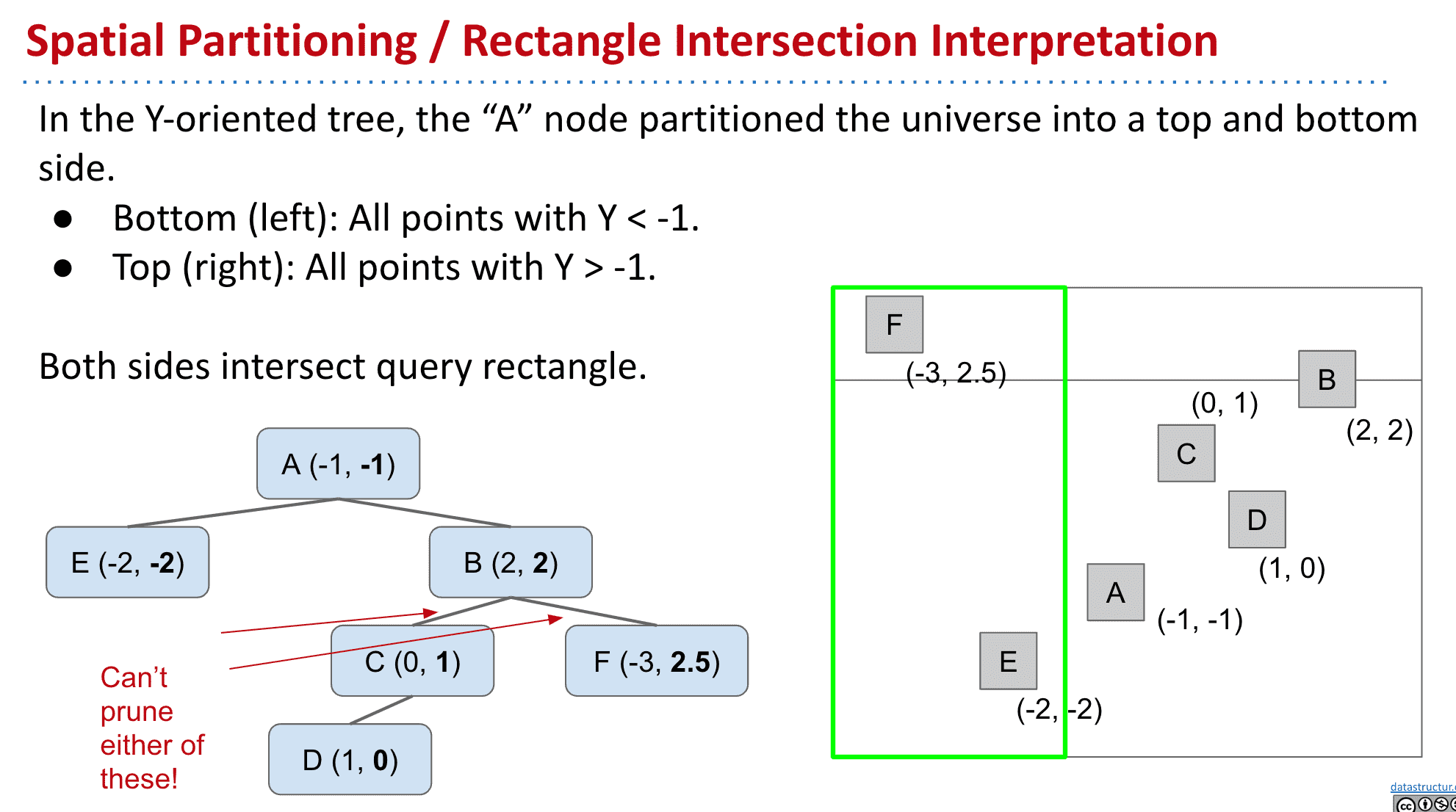
四叉树 Quadtree
四叉树的基本想法就是把一个顶点从拥有两个子节点变成四个,这样就可以容纳二维的数据了
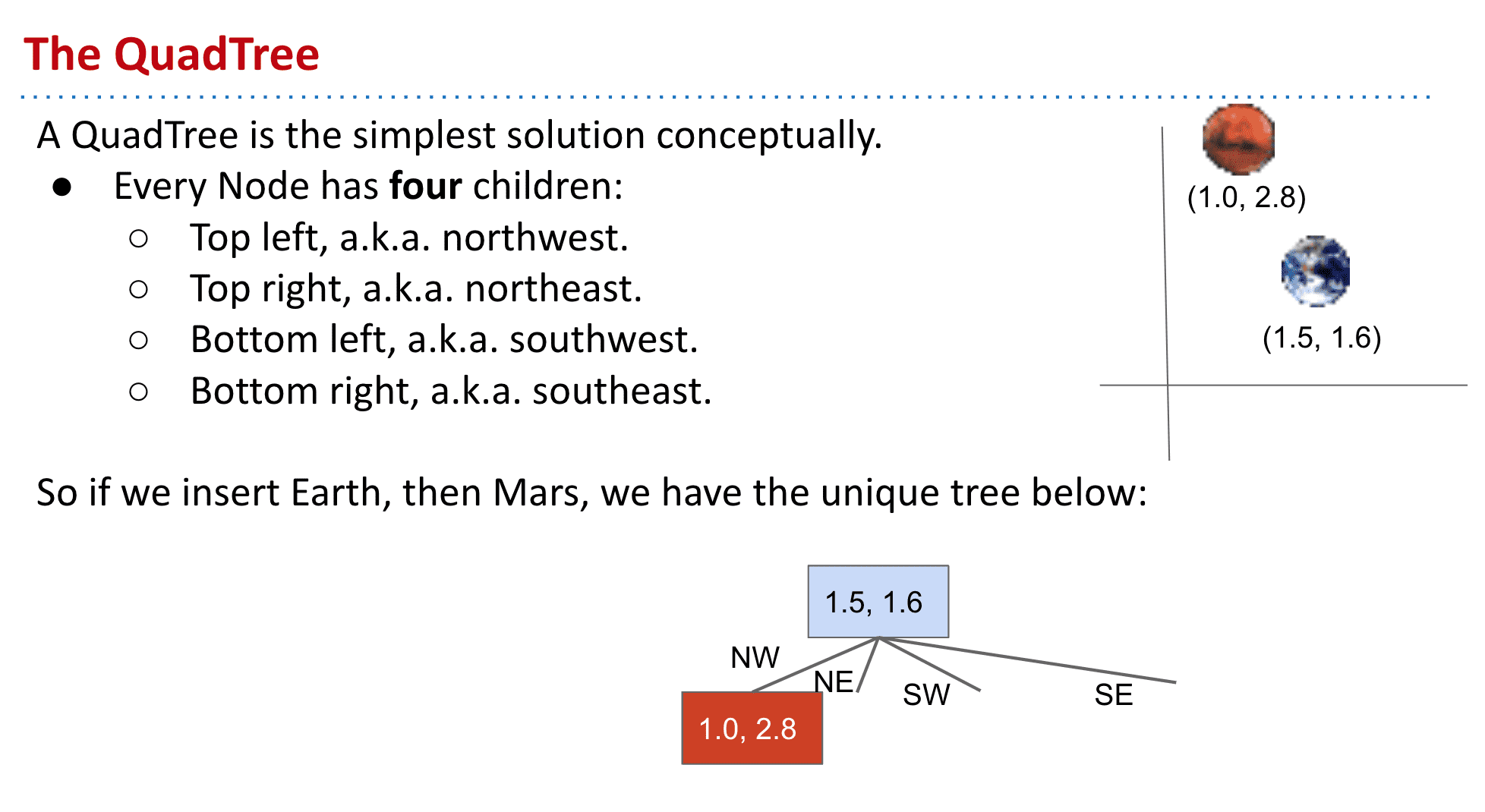
所以我们就可以按照x和y这样的二维数据来决定新的数据放到它的NW、NE、SE还是SW了,X决定东西,Y决定南北
其实回忆一下二叉树就像一个只有x的轴,而四叉树就像平面直角坐标系
另外这样之后我们就可以进行**空间分割 (Space partitioning)**了按照NW、NE、SE、SW把一个顶点的空间划为4个,这样就可以进行剪枝(pruning)从而像二叉树支持一维数据的各种操作一样,支持二维数据的各种操作了
Range Search
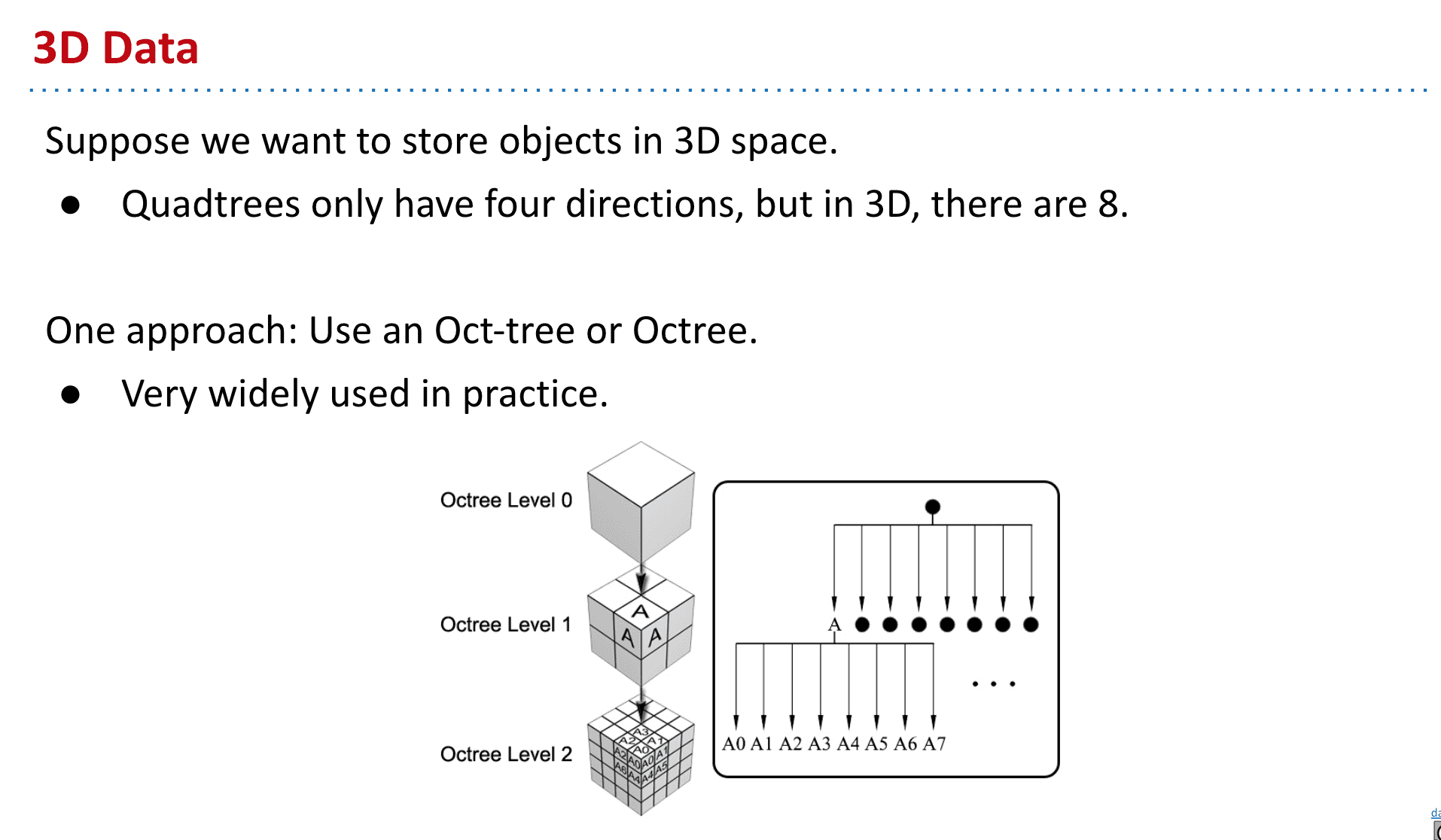
超过3维怎么办呢,就有了一个通用的结构k-d tree

k-d tree
(一下例子为二维数据时)
也就是k-dimensional tree的意思,可以支持任意高的维度
基本思想就是根据深度交替把空间分为左右或者上下然后插入新的值(更多维度就根据深度来切换X,Y,Z……)
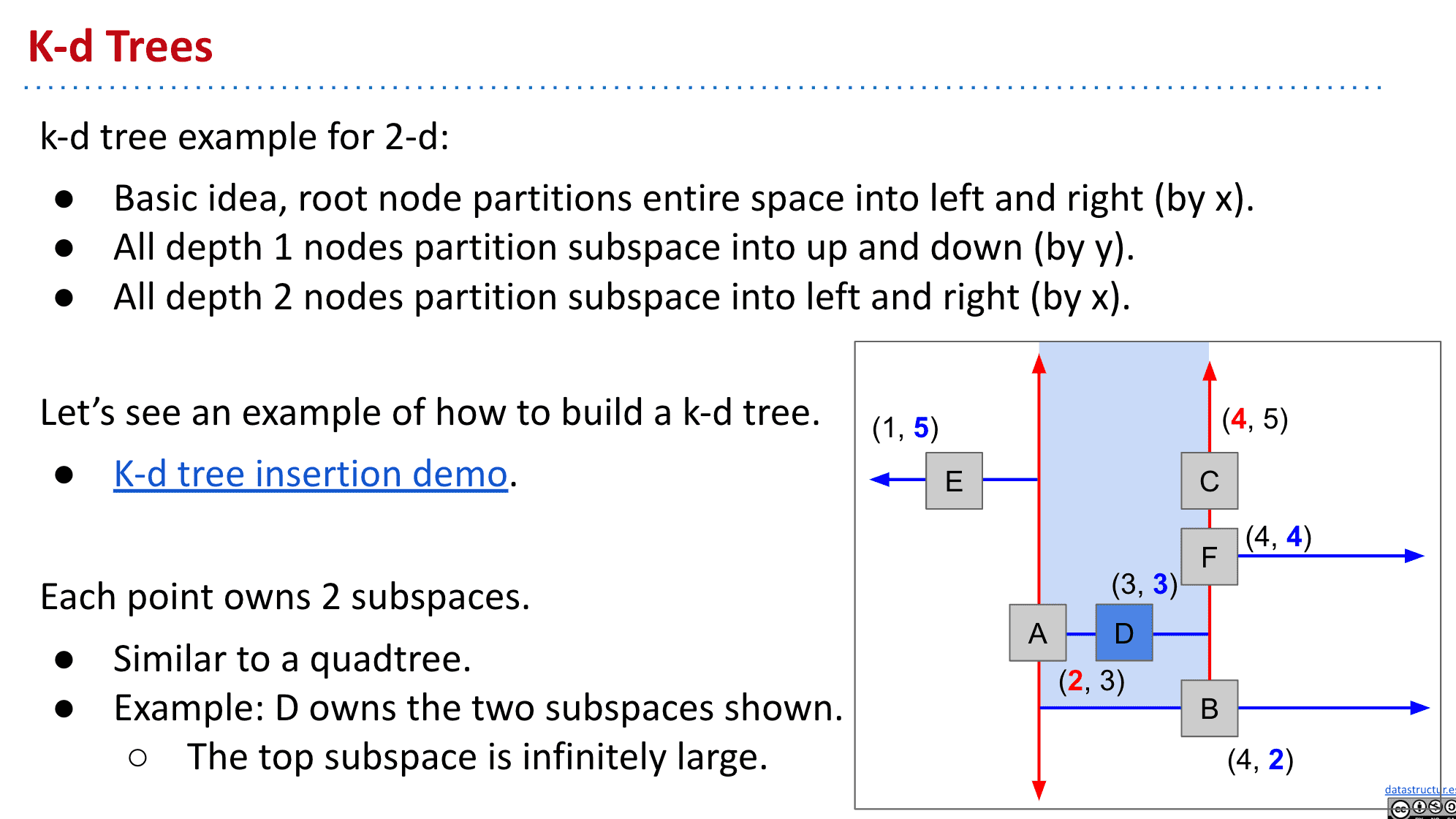
与四叉树类似,只是k-d tree的每一个顶点都分出了两个子空间
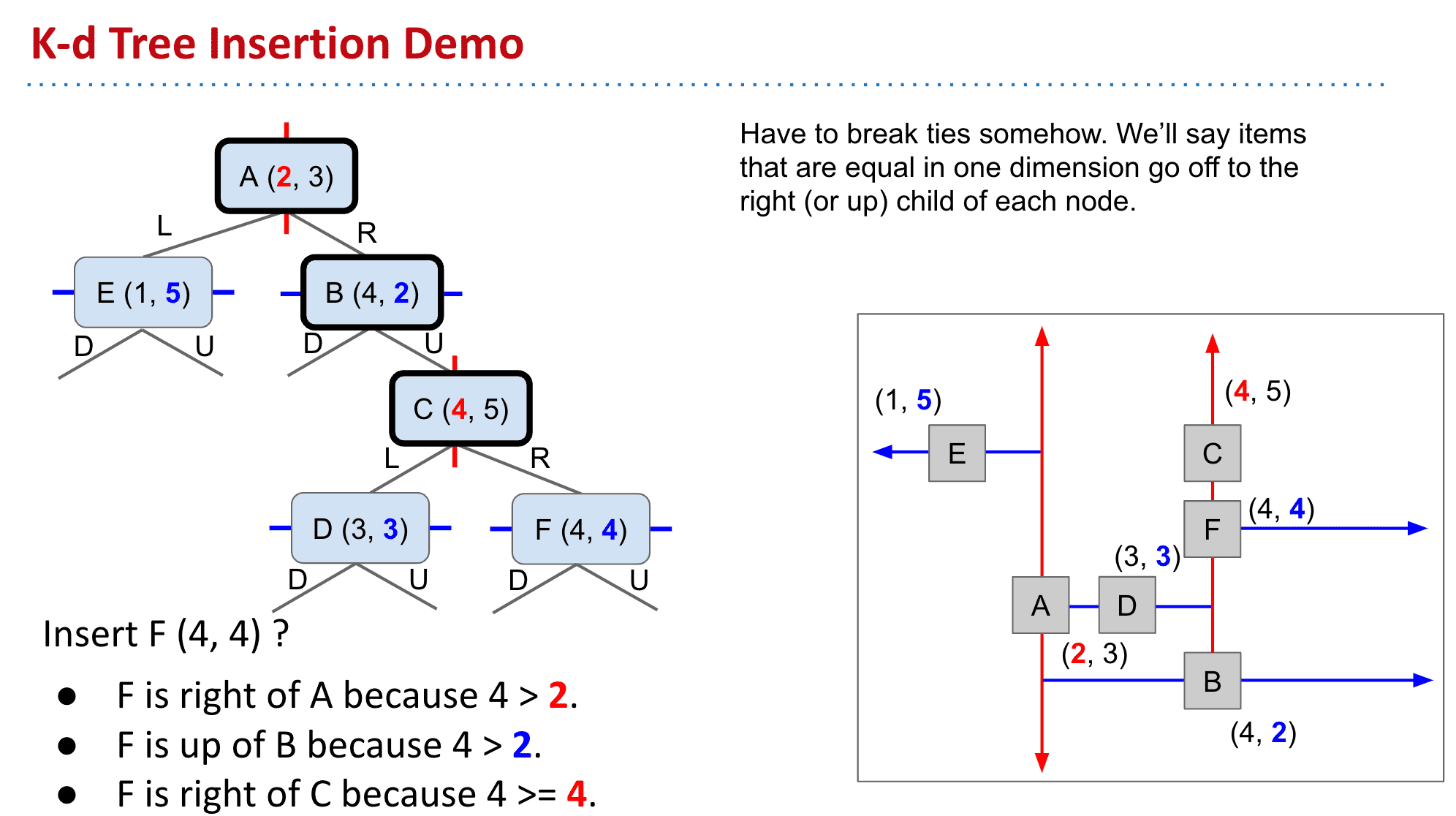
注意新加入的节点比较的时候,是哪一层就按照哪一层的重点值来比较,如果决定放入再比较另一个值
注意节点F虽然到C时该和C比较x值,但值却一样,按照规定一样的值就当作更大的值对待,所以F就放在C的R了
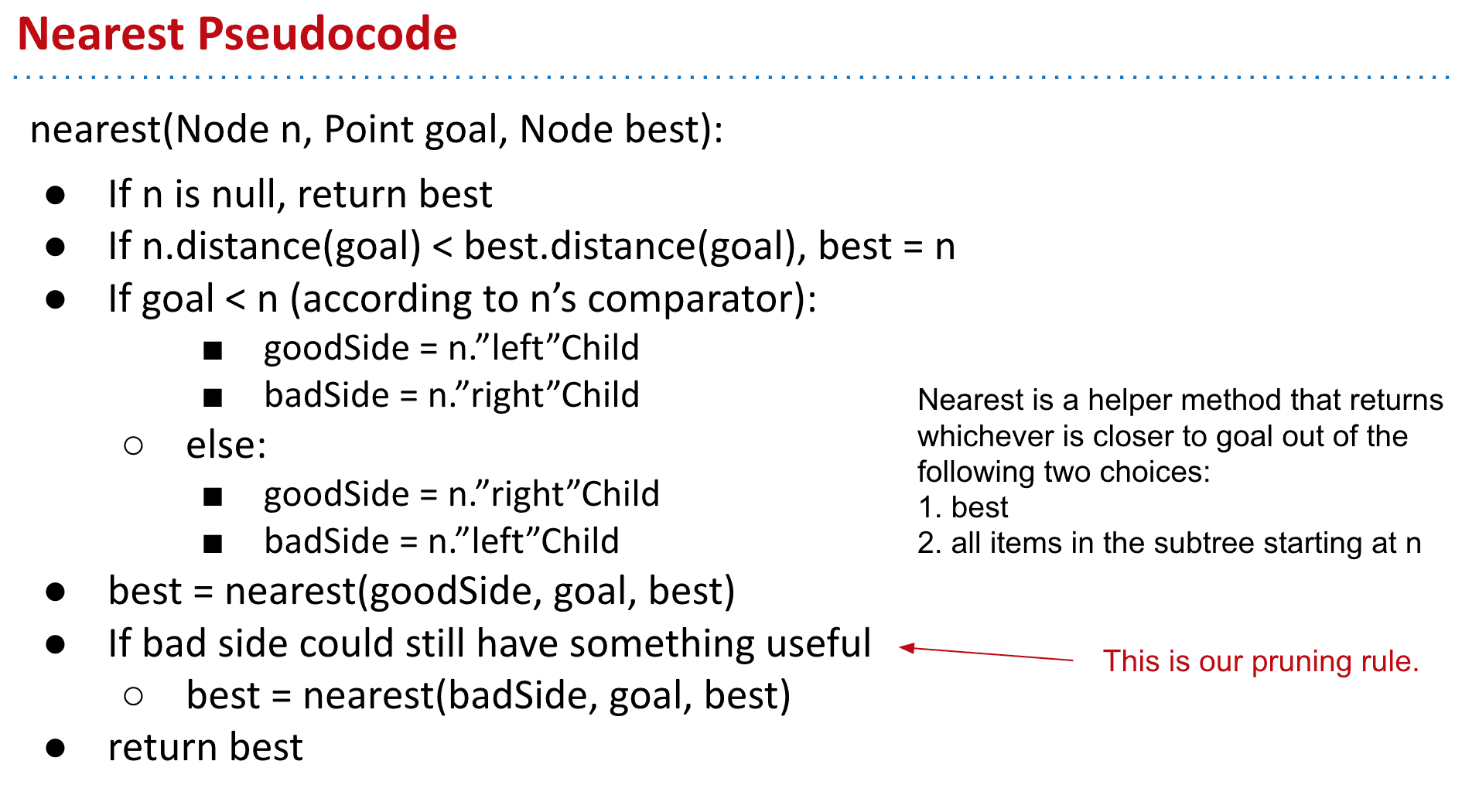
K-d Trees寻找最近点
因为不怎么懂,不做过多说明
总之就是通过一定找Good side而有条件地看Bad side找到理想的最近点
两种实现找最近点的伪代码

Uniform Partitioning
一种不适用tree而是划分区块来存储的结构 (不了解)同样也是spatial partitioning

Week 9
字典树 Trie
全称是Retrieval Tree,发音类似“try”
之前我们有许多方式可以实现Set和Map,而Trie又是另一种可以实现它们的方式
主要想法就是使用key值本身来存储数据,比如“sad”就是root-s-a-d,然后蓝色标号表示是一个结尾(实际可以给节点改变值来实现)这样就不会出现到底存没存“sa”的疑惑了
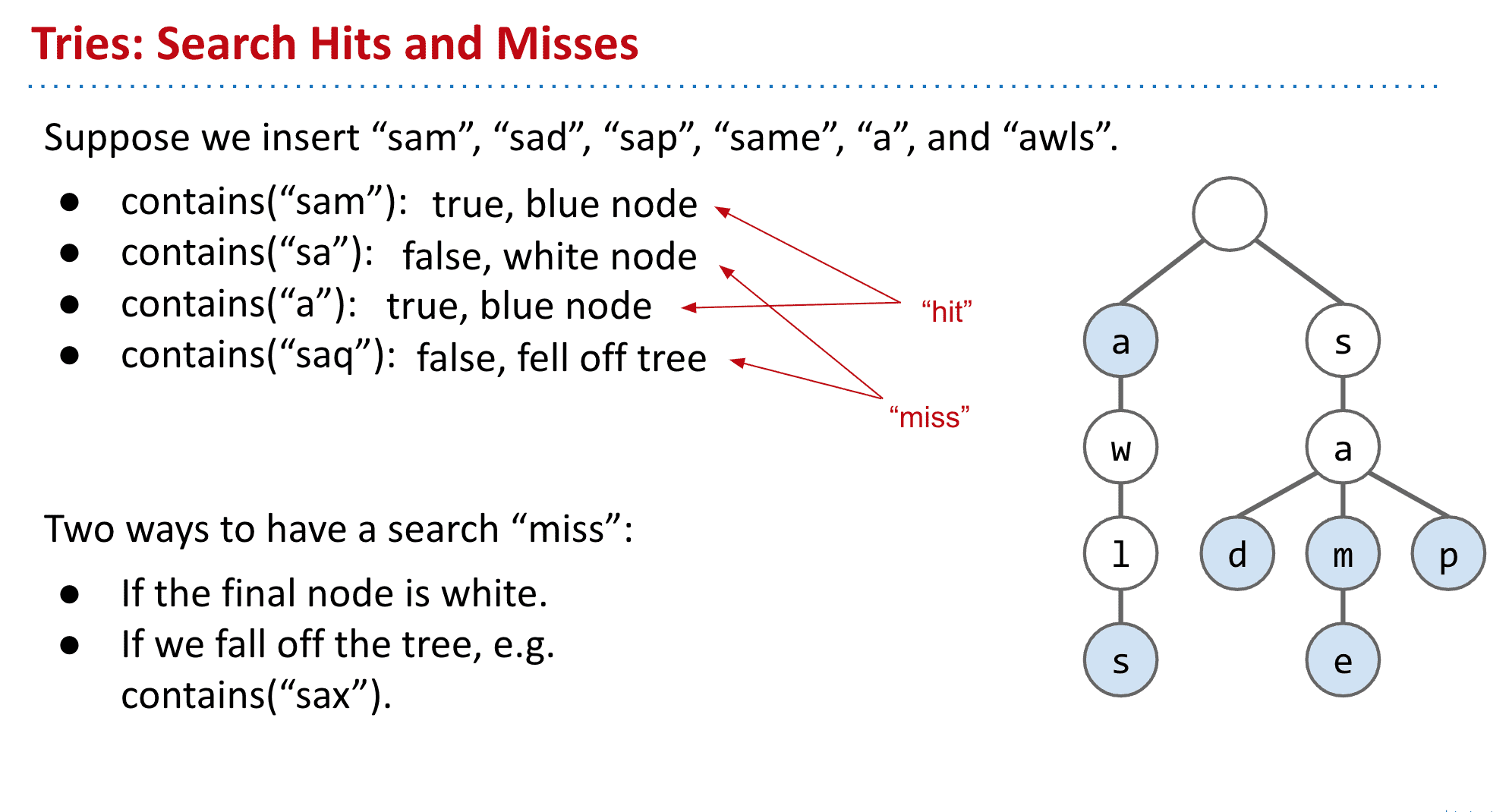
包含 “sam”, “sad”, “sap”, “same”, “a”, and “awls”, 不包含“aw”, “awl”, “sa”, 等
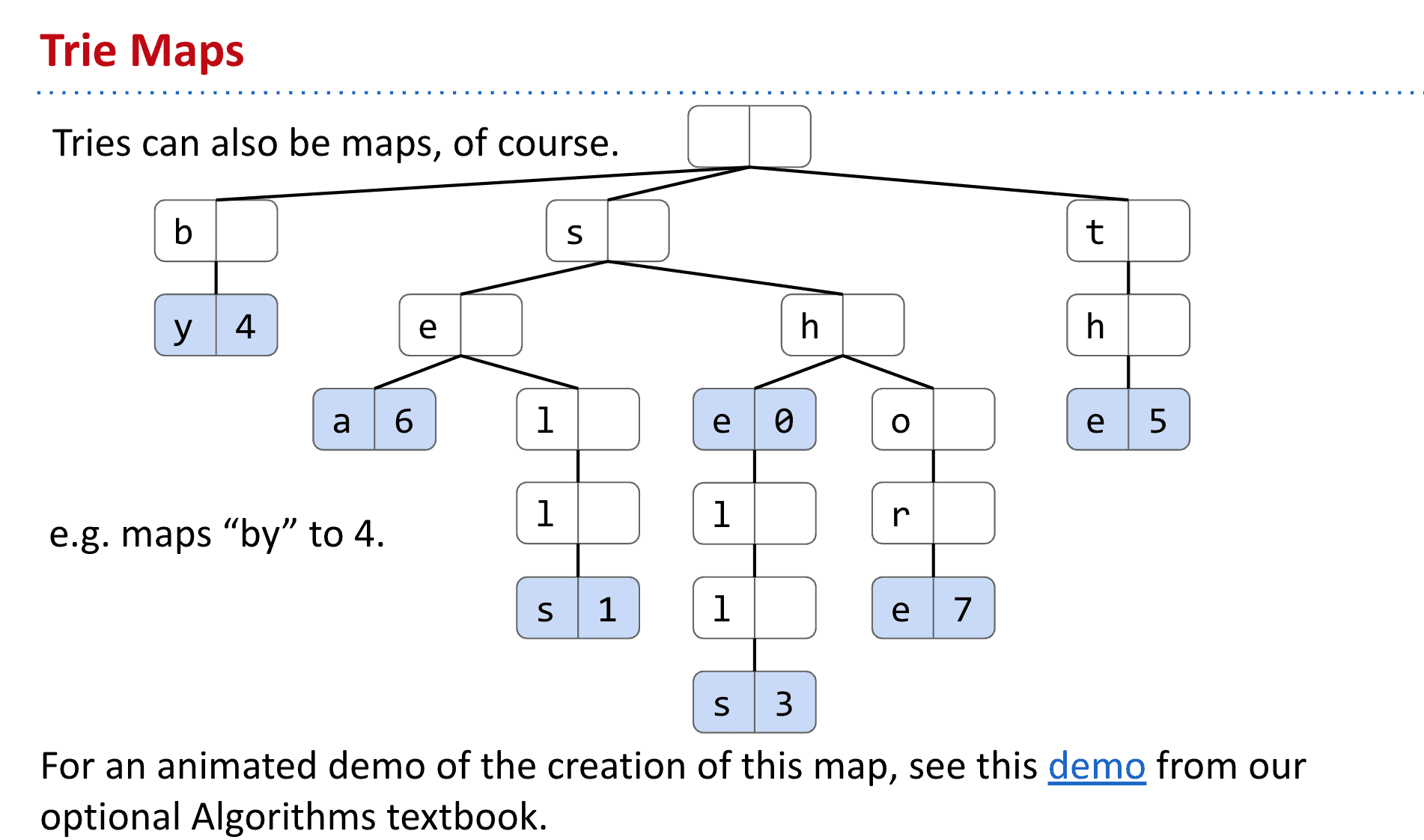
用trie实现Map也很简单,只需要加上存储值的位置就行了比如“shore”就对应7
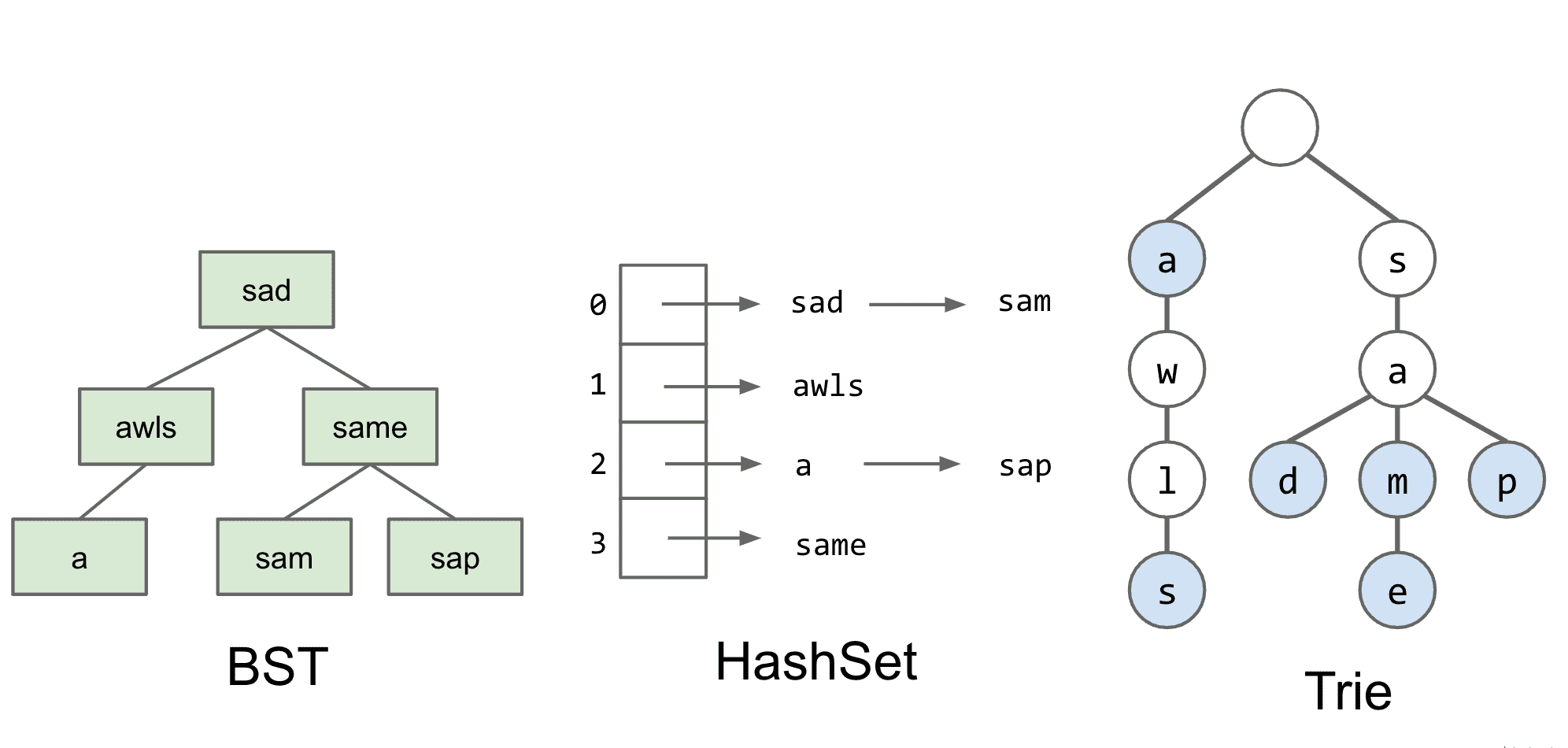
实现Set的几种方法对比
trie的基本实现
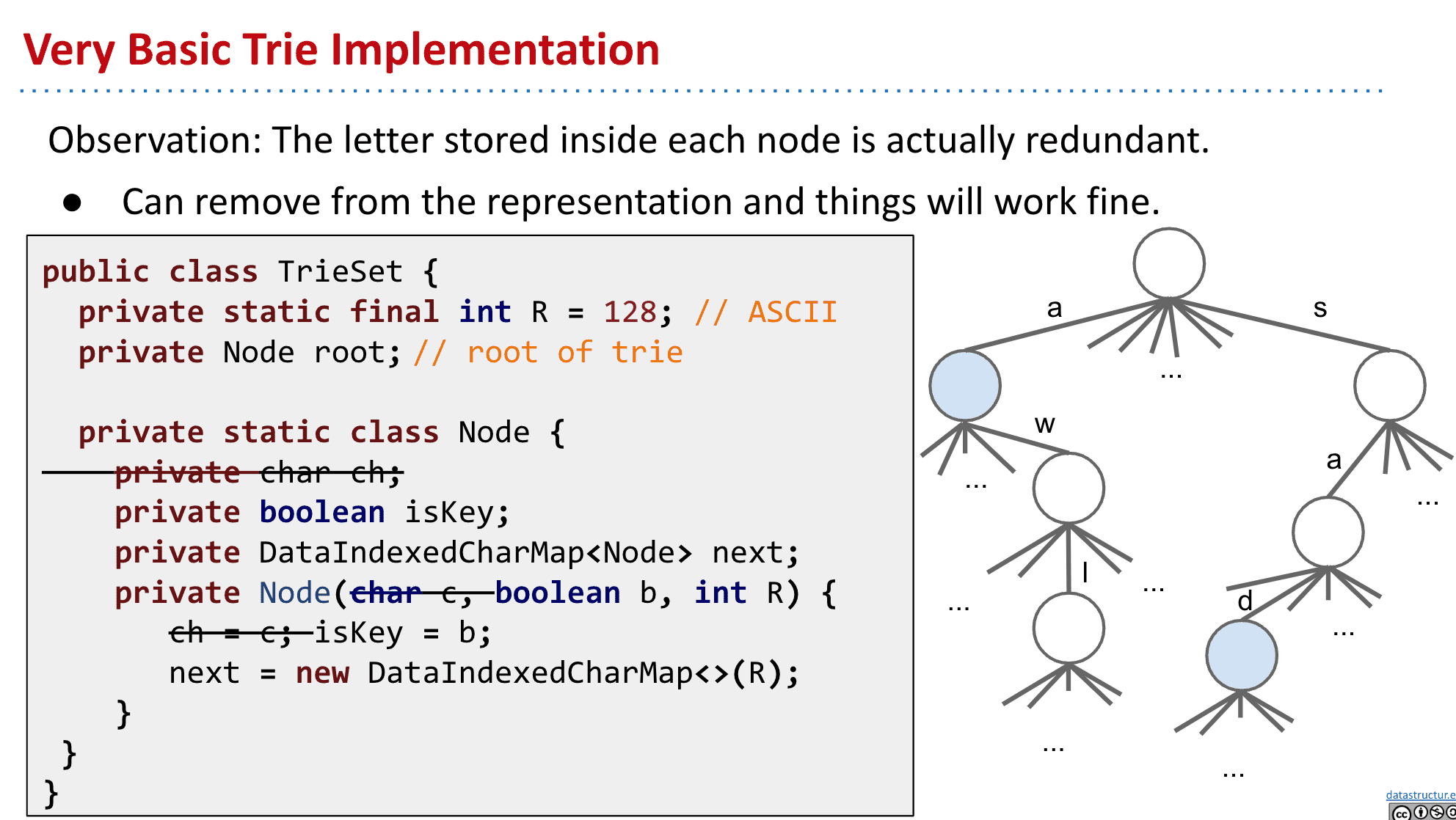
R代表有多少个子节点(更改它可以支持不同的字符集)
ch,也就是节点本身的字母可以删去,因为只有通过相应的链接才能到达该节点 这样可以减少冗余也就是“键不是直接保存在节点中,而是由节点在树中的位置决定”)
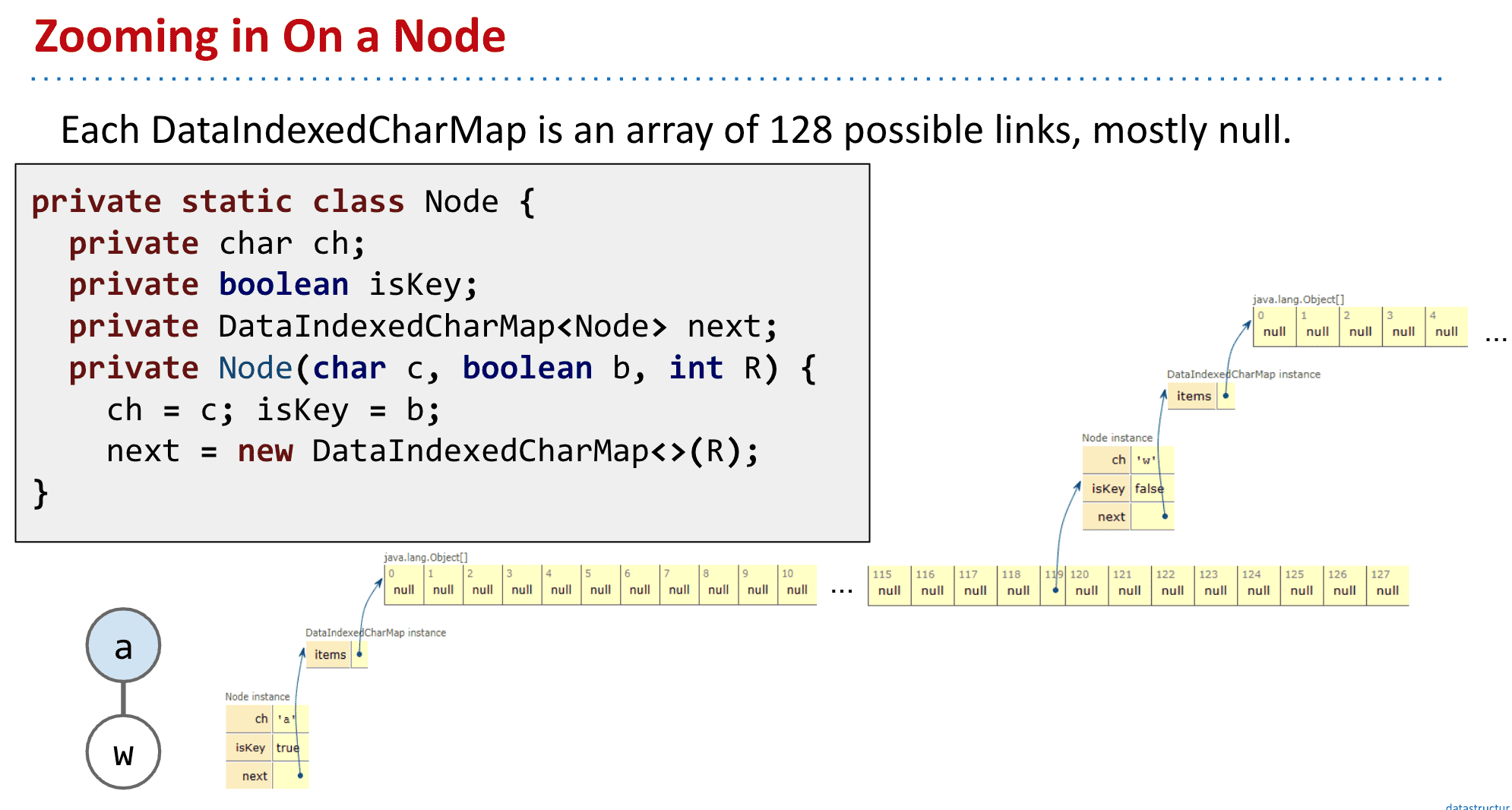
DataIndexedCharMap 代表子节点们
public class DataIndexedCharMap<V> {
private V[] items;
public DataIndexedCharMap(int R) {
items = (V[]) new Object[R];
}
...
}
isKey表示该节点是否是一个结尾(也就是标记成蓝色的节点)
能看出来这样需要大量的内存给空的地方
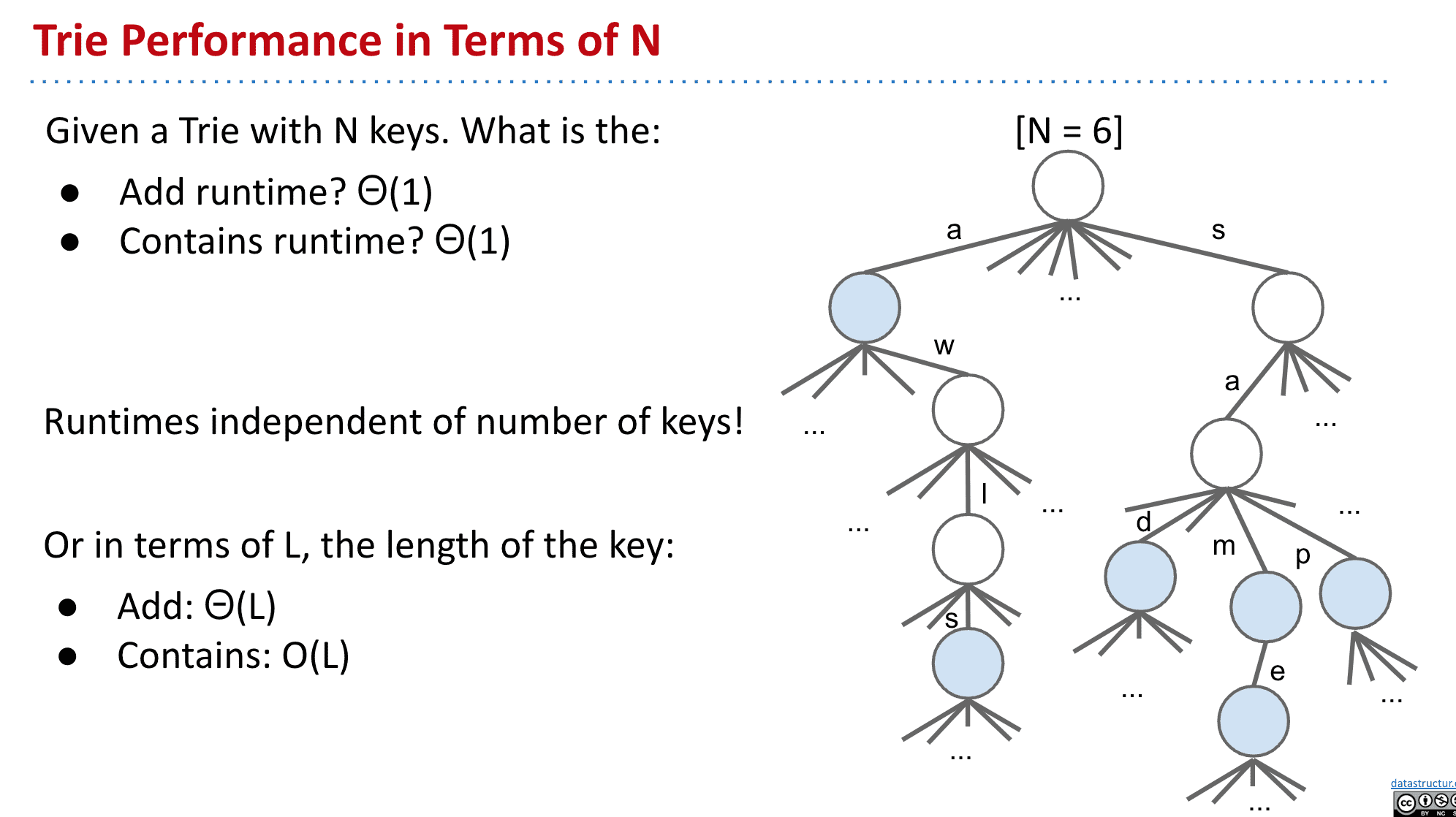
效率和运行时间
由于不需要额外寻找其他节点,所以添加和查询都是固定的时间
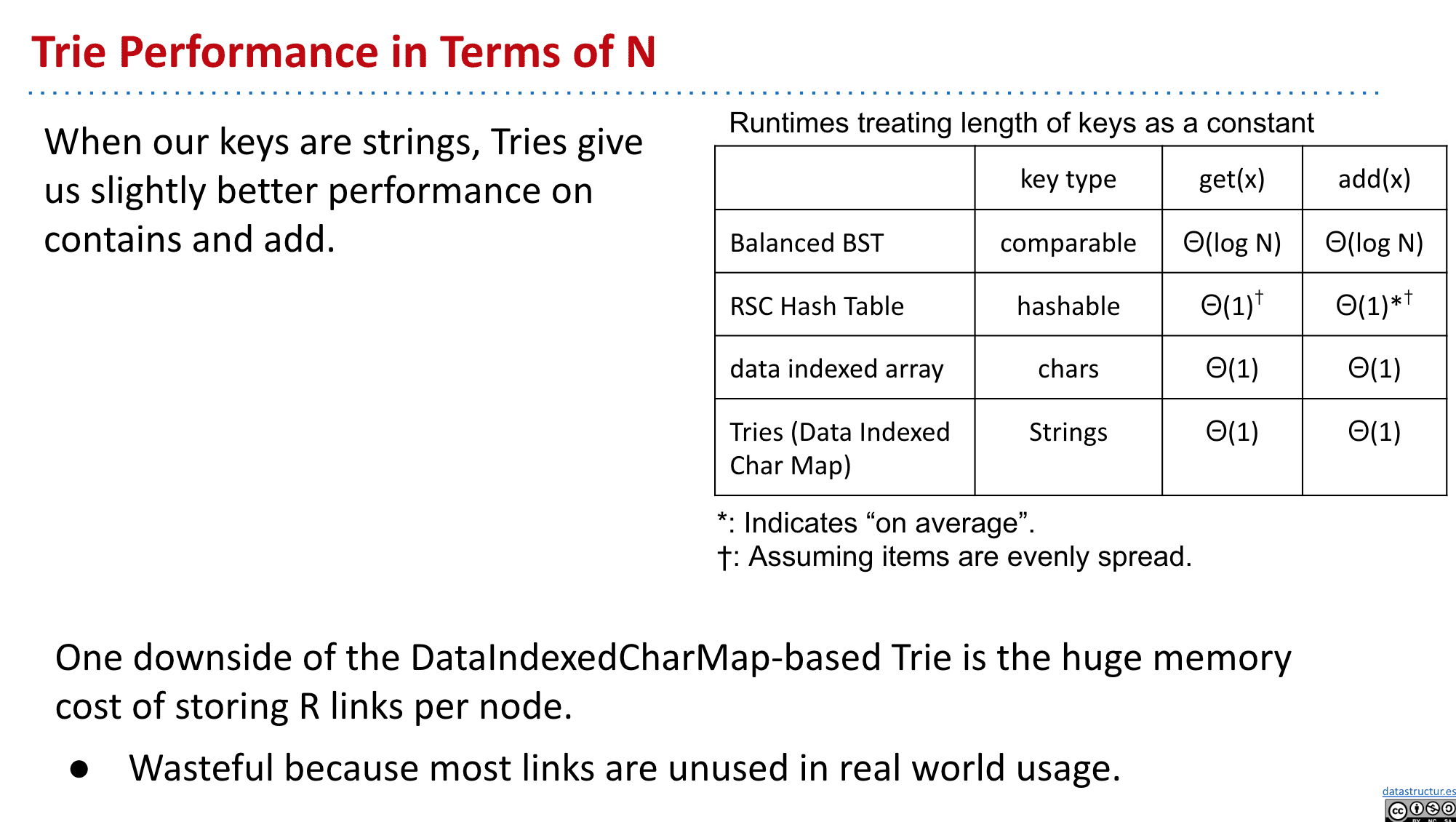
和其他实现对比有速度优势!
速度很快并且恒定,但缺点是会使用大量存储给用不到的节点
改变指向子节点的策略
上面说到这种存下全部子节点的方式,虽然速度很快,但是会浪费大量内存
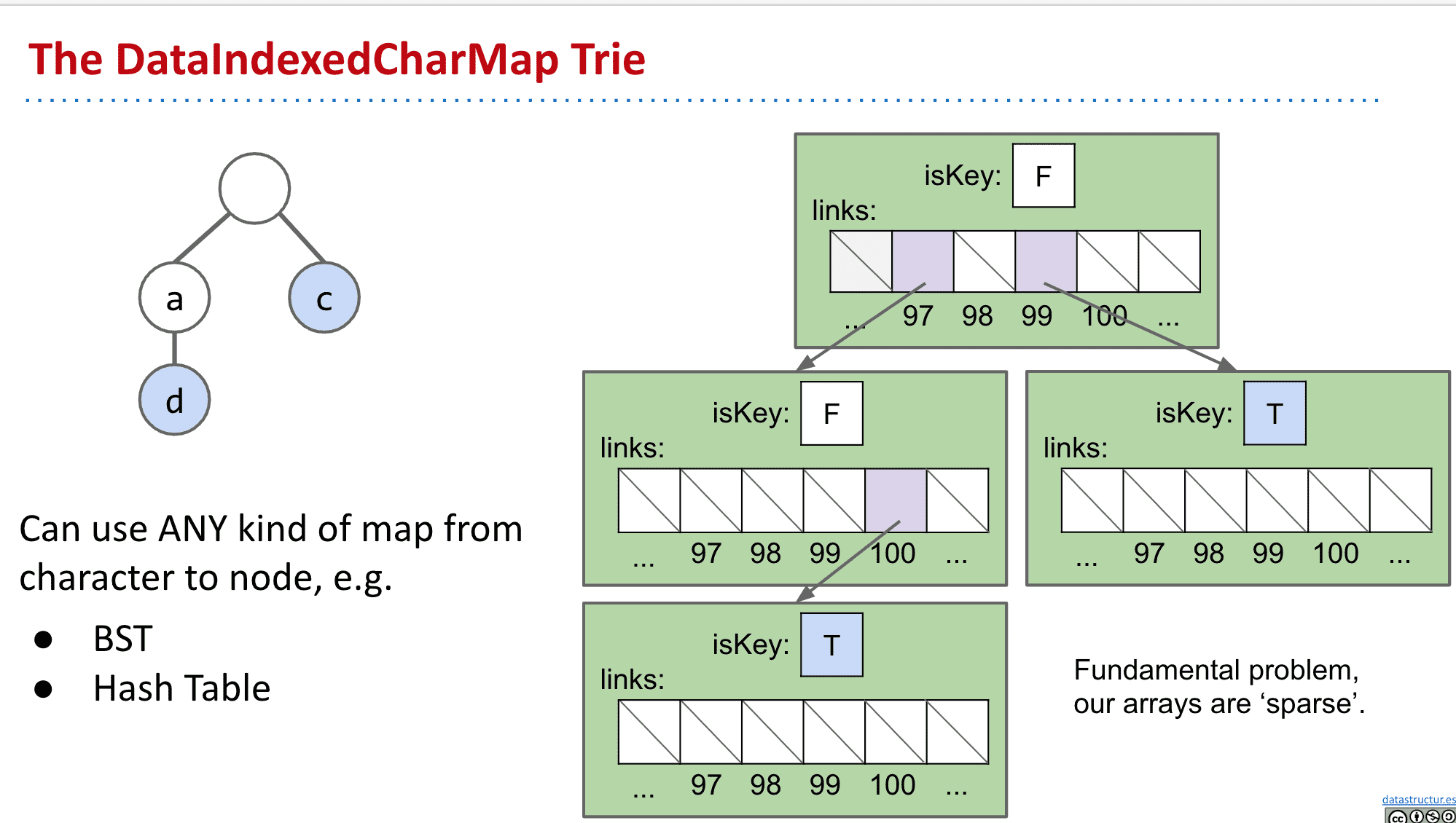
所以可以使用Hash table或者BST来追踪子代
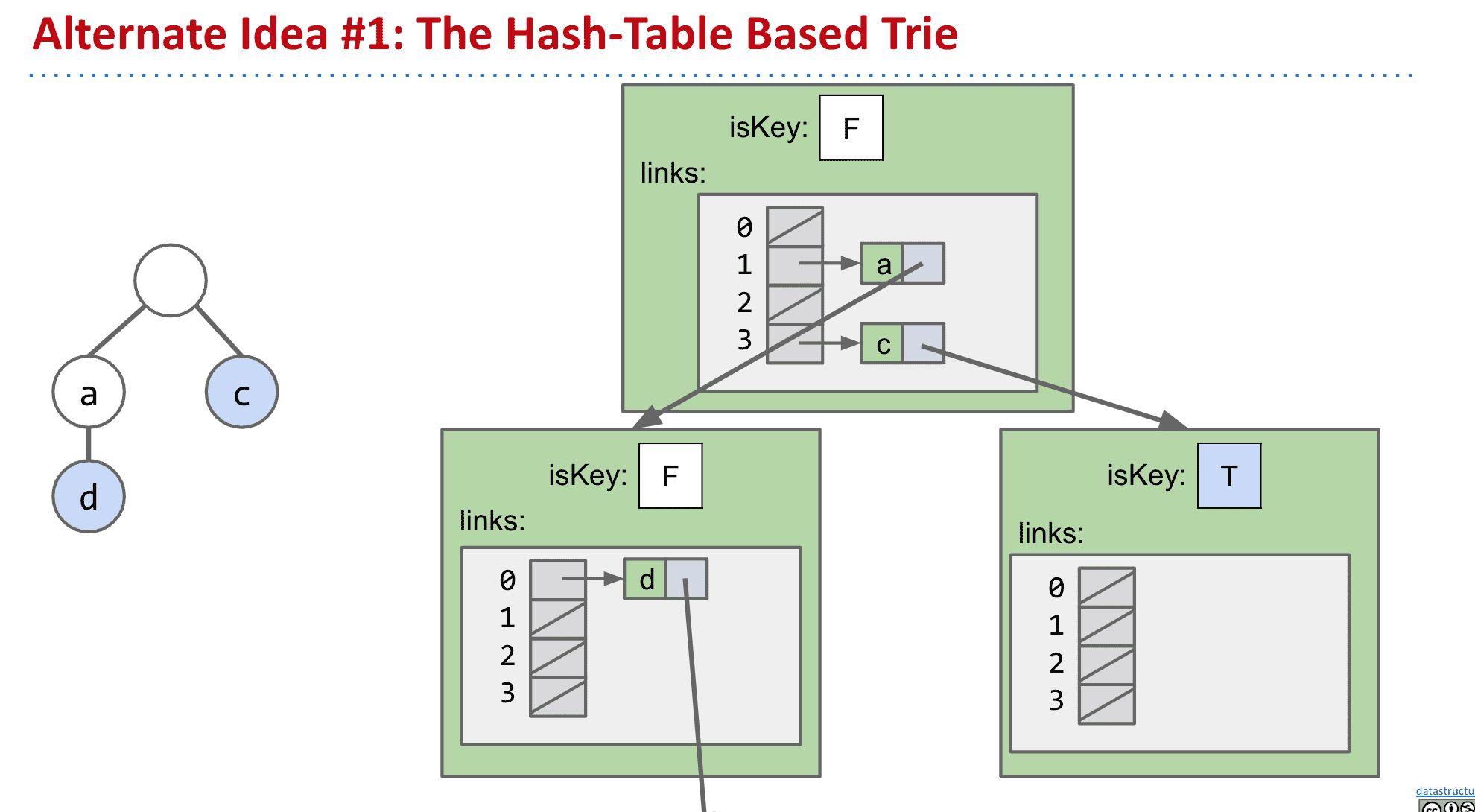
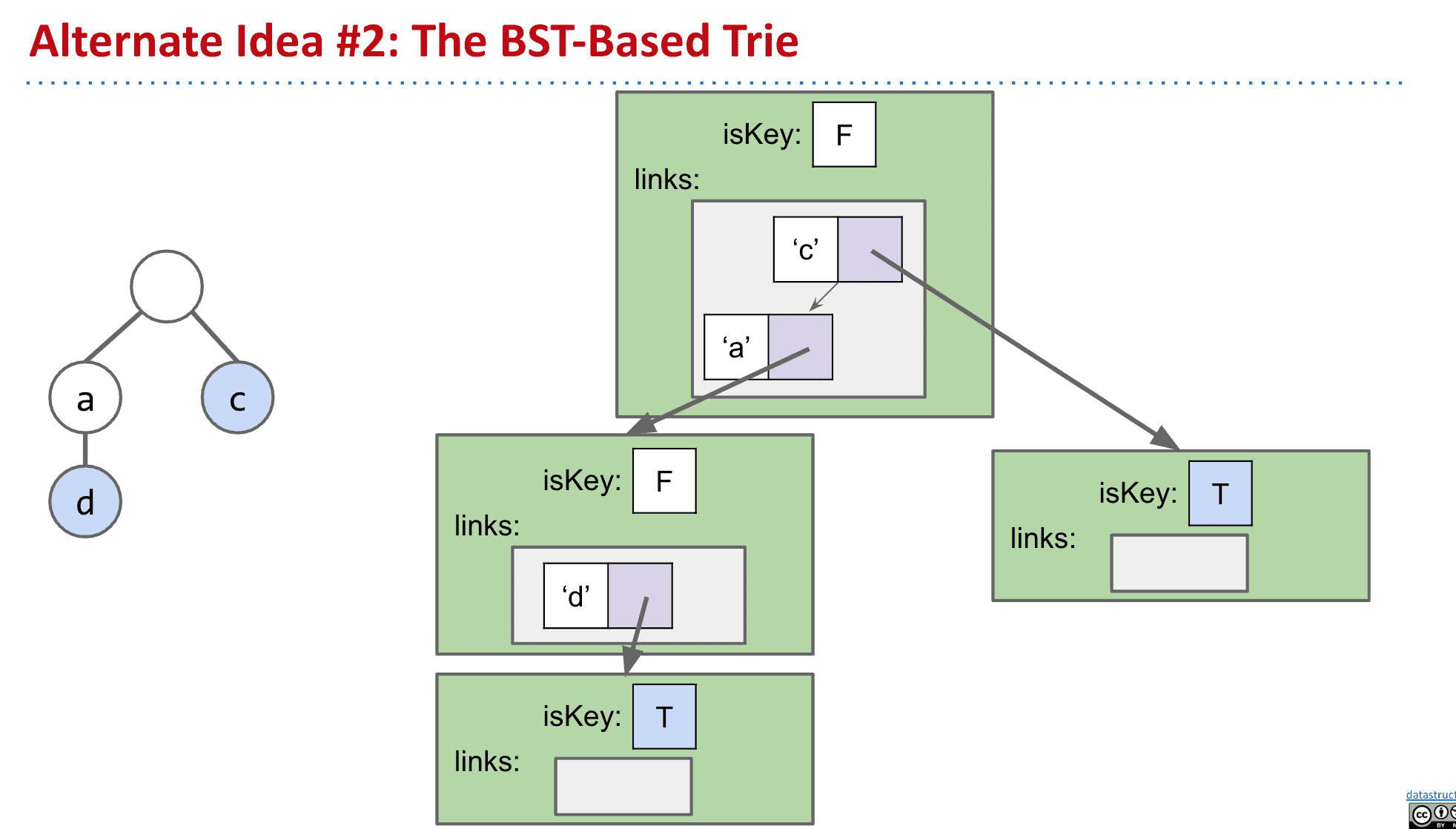
不过这样虽然内存使用小了很多很多,但运行时间会稍微增加
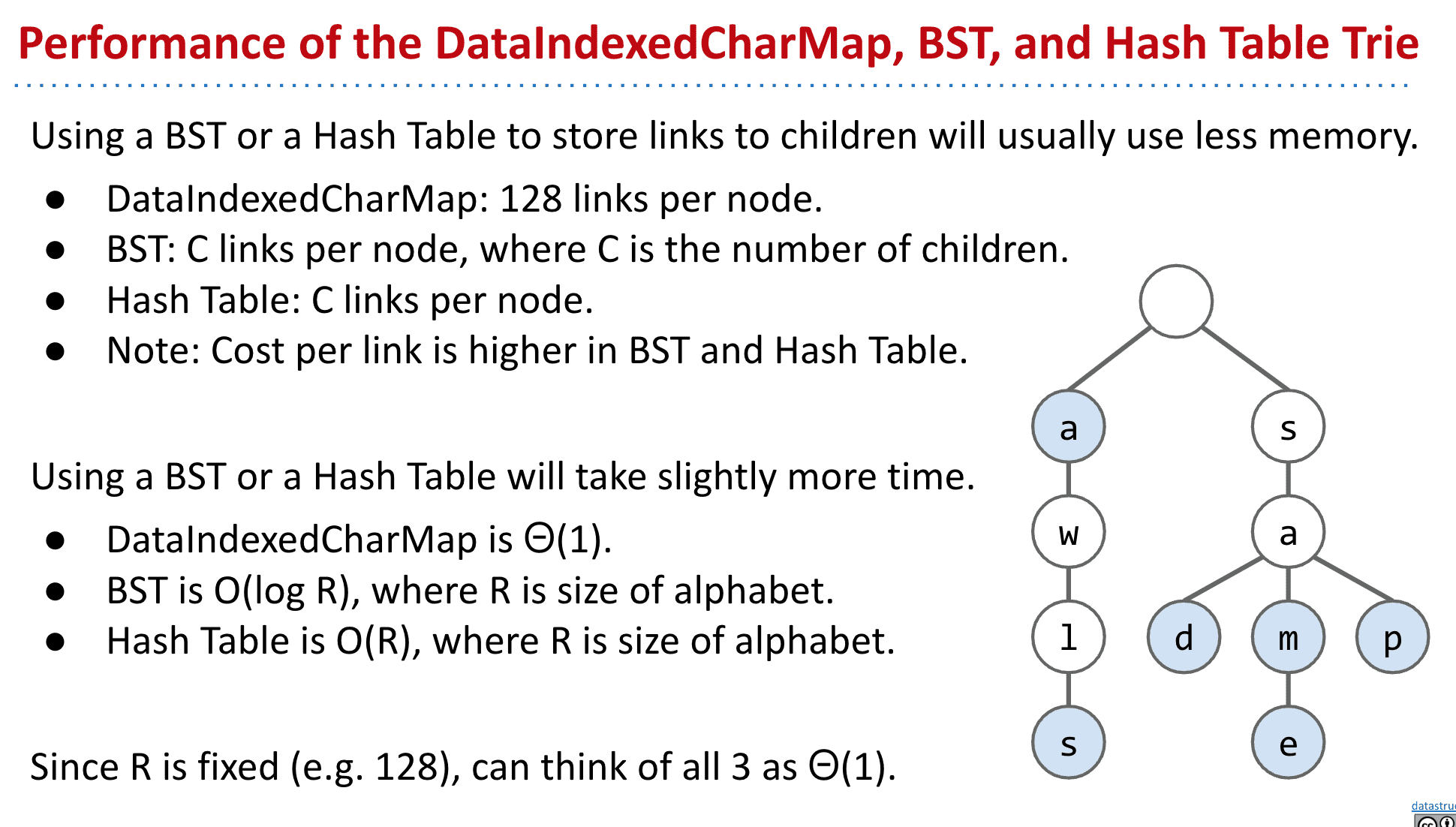
Trie的操作 Trie String Operations
理论上渐进式的速度改进是不错的。但Trie的主要吸引力在于它们能够有效地支持String的特定操作,如前缀匹配(prefix matchng)
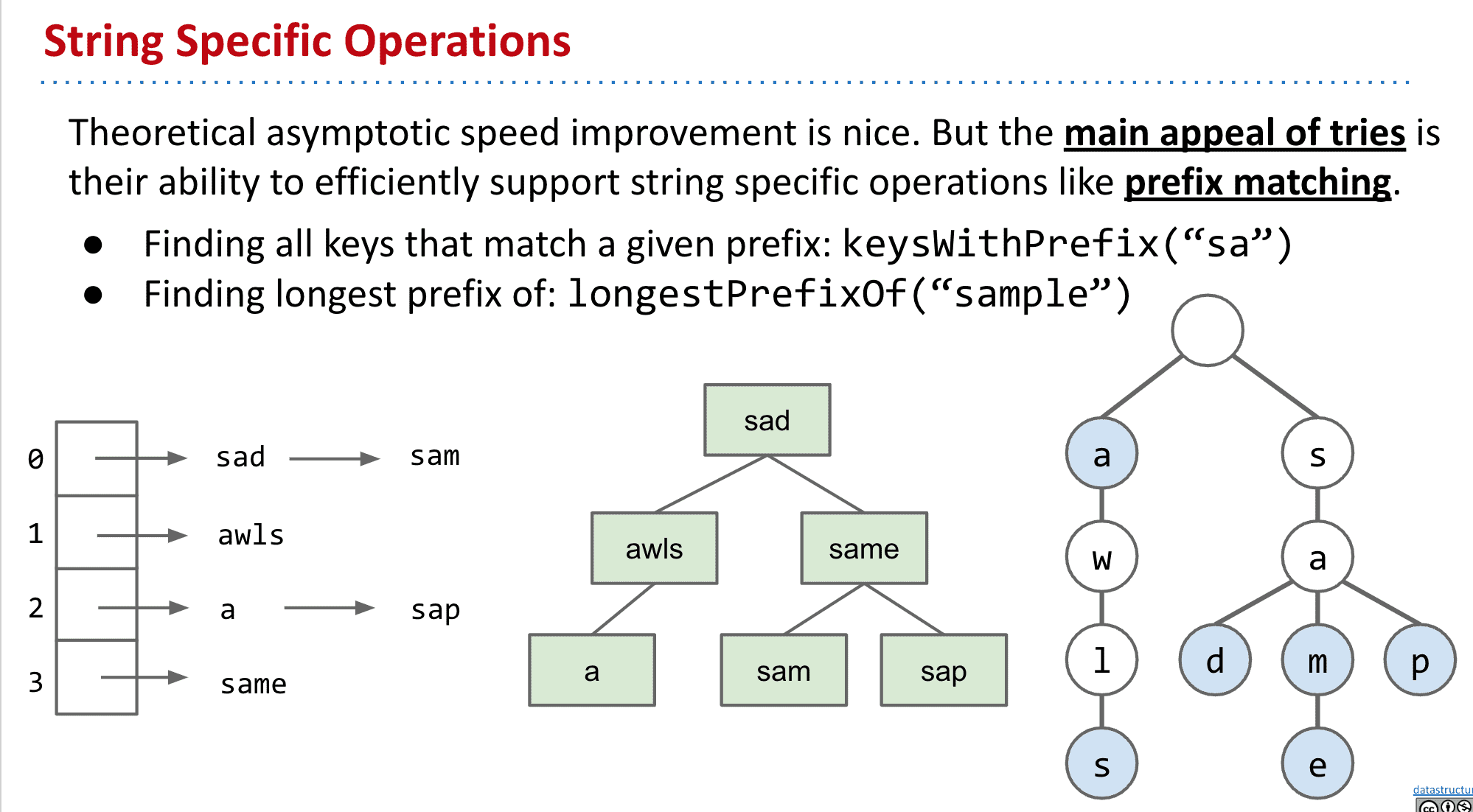
比如找到以“sa”开头的String,或者trie中拥有的最长的“sample”的前缀
伪代码:找到trie中的所有值:

通过递归不断向下运算,并且把符合的词加入list
找到以某个前缀开头的所有值:

与上一个类似,知识把root定在想要找的前缀上
上面这些应用都是Trie相比以前的BST、Map等拥有的优势,可以快速进行字符串相关的操作
自动补全 Autocomplete
像在搜索引擎中常见的输入几个字就提示可能的结果,就是Trie的一种应用
比如一个Trie形式的map拥有权值,按照AI计算出的权值向用户推荐最有可能的补全结果
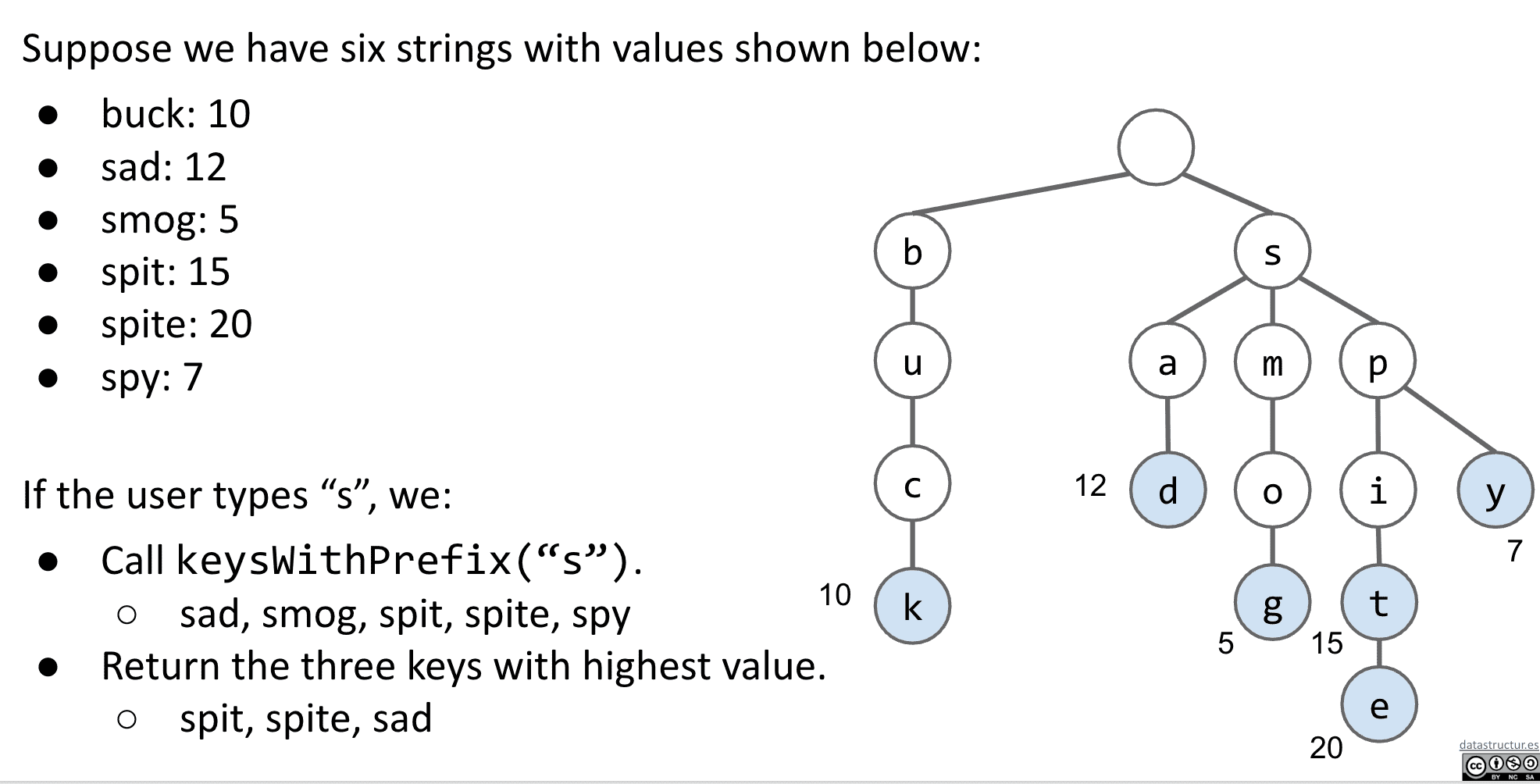
但是我们可能遇到只输入如“b”的话,有数百万乃至更多结果,如果要返回最高的几个的话计算量就太大了

所以我们不止加入权值,还加入子代最高的权值
也就是best值,记录下面最高的权值
这样就可以快速找到最高的几个权值key,并返回给用户了
(可以把他们使用PQ来决定访问顺序,比如s的PQ就是p、a、m)
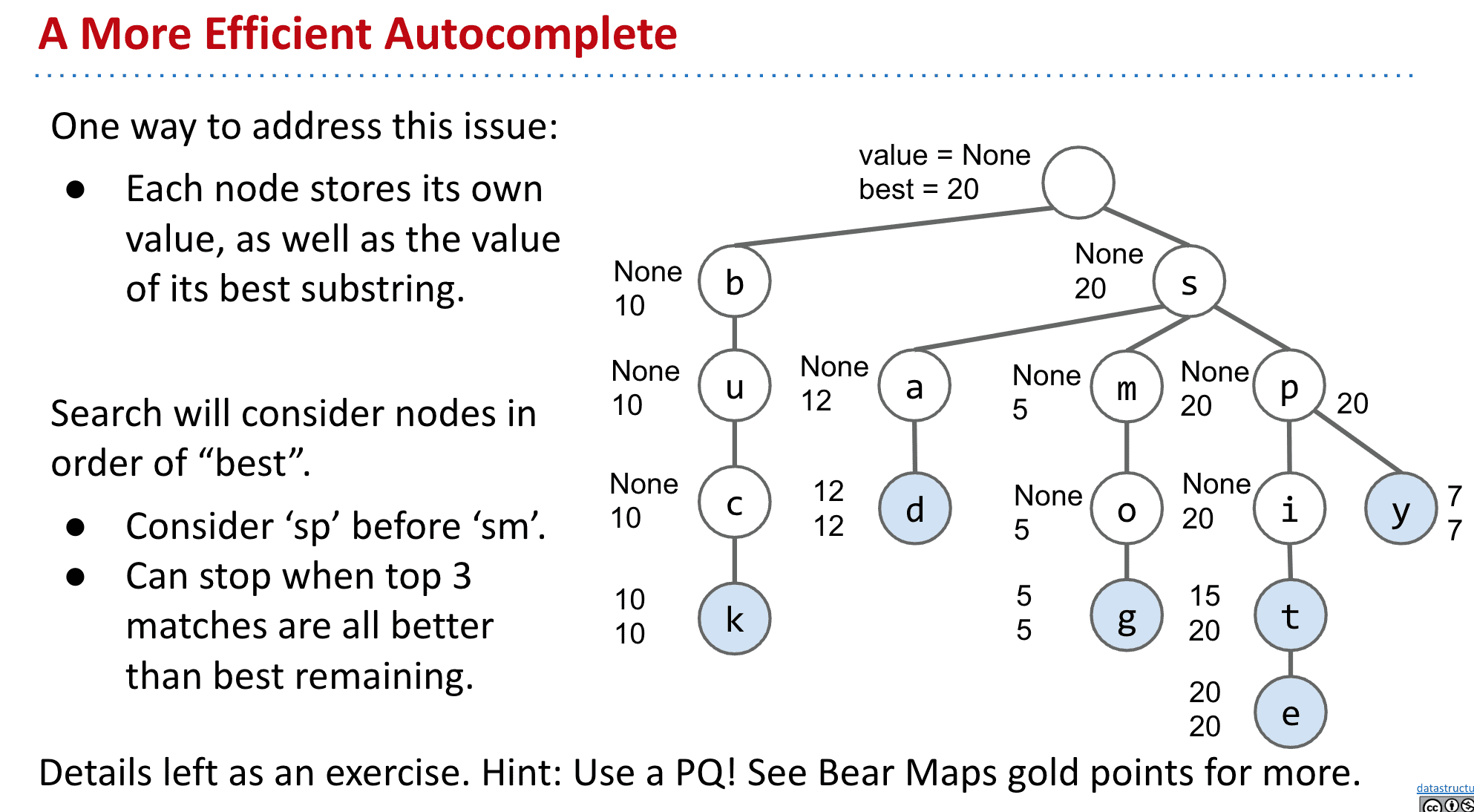
更进一步:
可以看到中间有许多不是key的节点,所以可以进行压缩节省时间和内存
这种结构被称为基数树 (Radix tree)
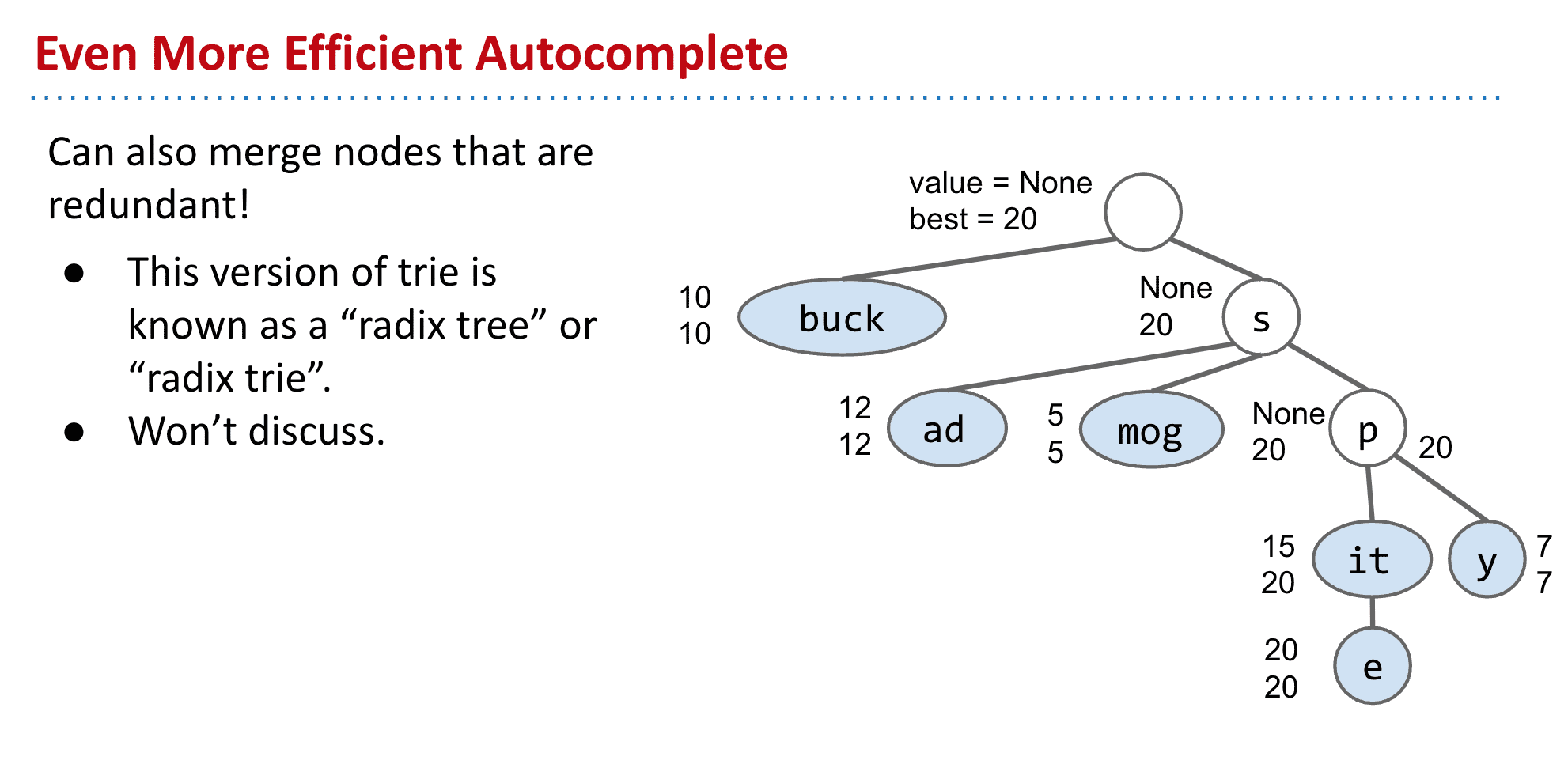
总结
trie理论上性能比BST、Map好,真正的优势是各种String操作,比如找前缀等来支持如自动补全等功能
还有解压缩时编码到字符的过程使用trie也会很快
另外各种数据结构融合也能来更好的效果比如trie和pq和之前的各种trie的子节点实现方式
当然除了trie外还有后缀树Suffix Trees (Link)、无环确定有限状态自动机DAWG (Link)等各种不同用途的数据结构

软件工程 Software Engineering I
之所以有这个内容是之前大部分的编程内容都是小规模的,根据指引完成的(project2、3除外)
但对于真正编程来讲并不是这样的,所以要教导怎么样面对大的项目
复杂度 Complexity Defined
编程是一种几乎纯粹的创造性的行为
我们在构建系统时面临的最大限制是能够理解我们正在构建的东西!这一点与其他学科非常不同
随着真实程序的维护,它们会获得更多的功能和复杂性(也就是所谓的屎山形成吧,一开始哪怕很简洁后面也会慢慢复杂,所以不可避免但可以尽量减少)
随着时间的推移,程序员在未来进行修改时,要理解所有相关的部分会变得更加困难
各种工具可以帮助我们更容易面对复杂性
最重要的目标就是保持我的软件“simple”
管理复杂度
- 保持代码简单和明显
尽量减少特殊情况(比如哨兵节点) - 模块化(封装)
在模块化设计中,一个 "模块 "的创建者可以使用其他模块而不知道它们是如何工作的
复杂度定义
究竟什么是复杂度?Ousterhout这样定义它:"复杂性是与软件系统的结构有关的任何东西,它使人难以理解和修改系统"。
比如:
理解代码如何工作。
进行小的改进所需的时间
找到需要修改的地方以进行改进。
难以修复一个错误而不引入另一个错误。
"如果一个软件系统很难理解和修改,那么它就很复杂。如果它很容易理解和修改,那么它就很简单"。
所以像魔法数字、大量重复、不清楚的命名和没有注释等都将增加复杂度
在写真正的项目时,代码能够工作是不够的,必须注意增加复杂度的苗头并且及时重构,写的时候也要想象未来可能会怎么修改代码
拓扑排序 Topological sorting
假设有0~7项任务,而有箭头的任务必须在指向它的节点后发生,有什么算法可以给出顺序、从哪个点开始算法
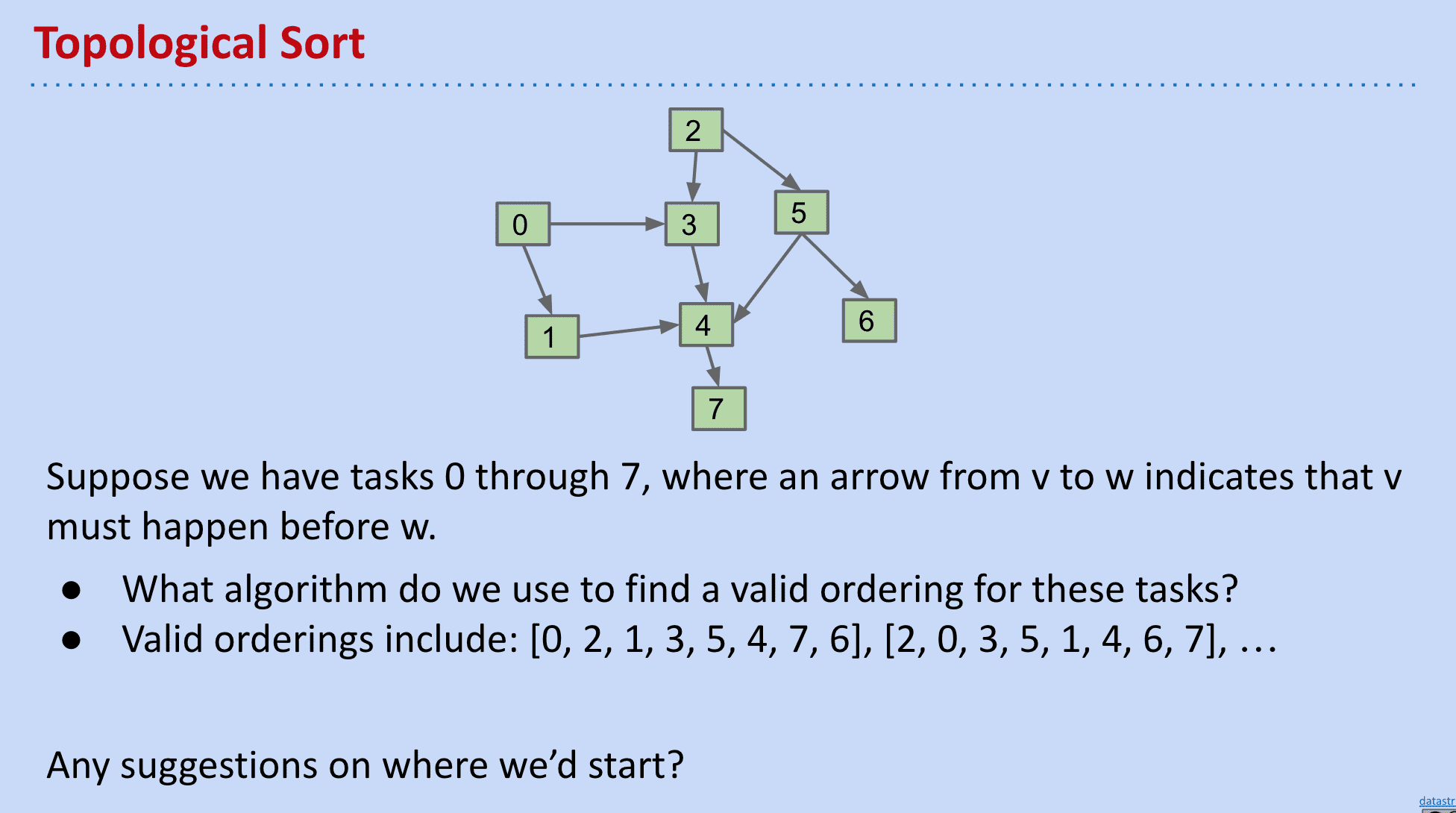
可以使用DFS从indegree(引入次数、入度)为0的点开始,并且完成后切换到另一个indegree为0的点后不清除标记(防止重复)
按Postorder的方式把DFS访问记录到list
然后翻转上面的list就得到了拓扑顺序
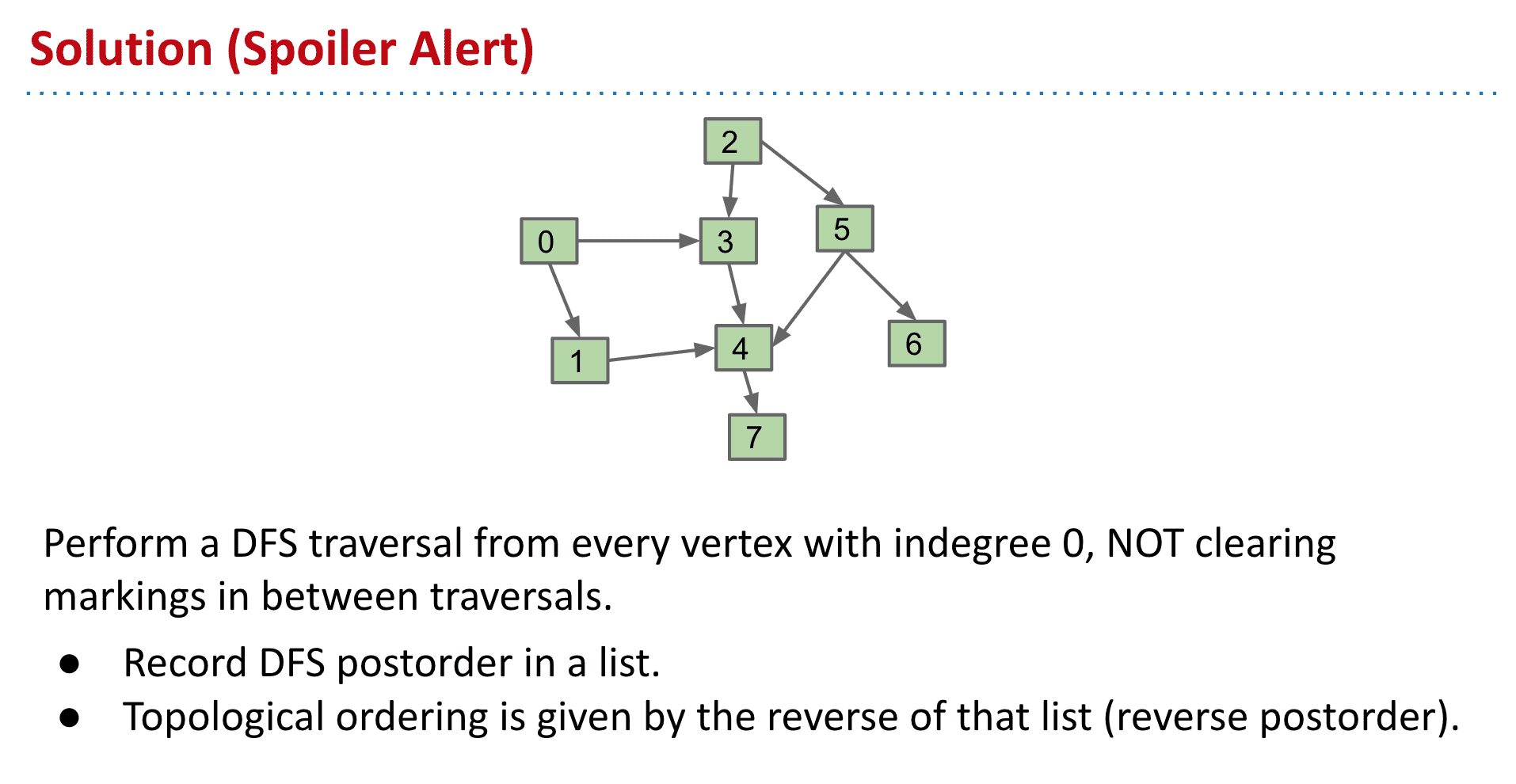
这种拓扑的情况下,不存在节点的循环
访问顺序
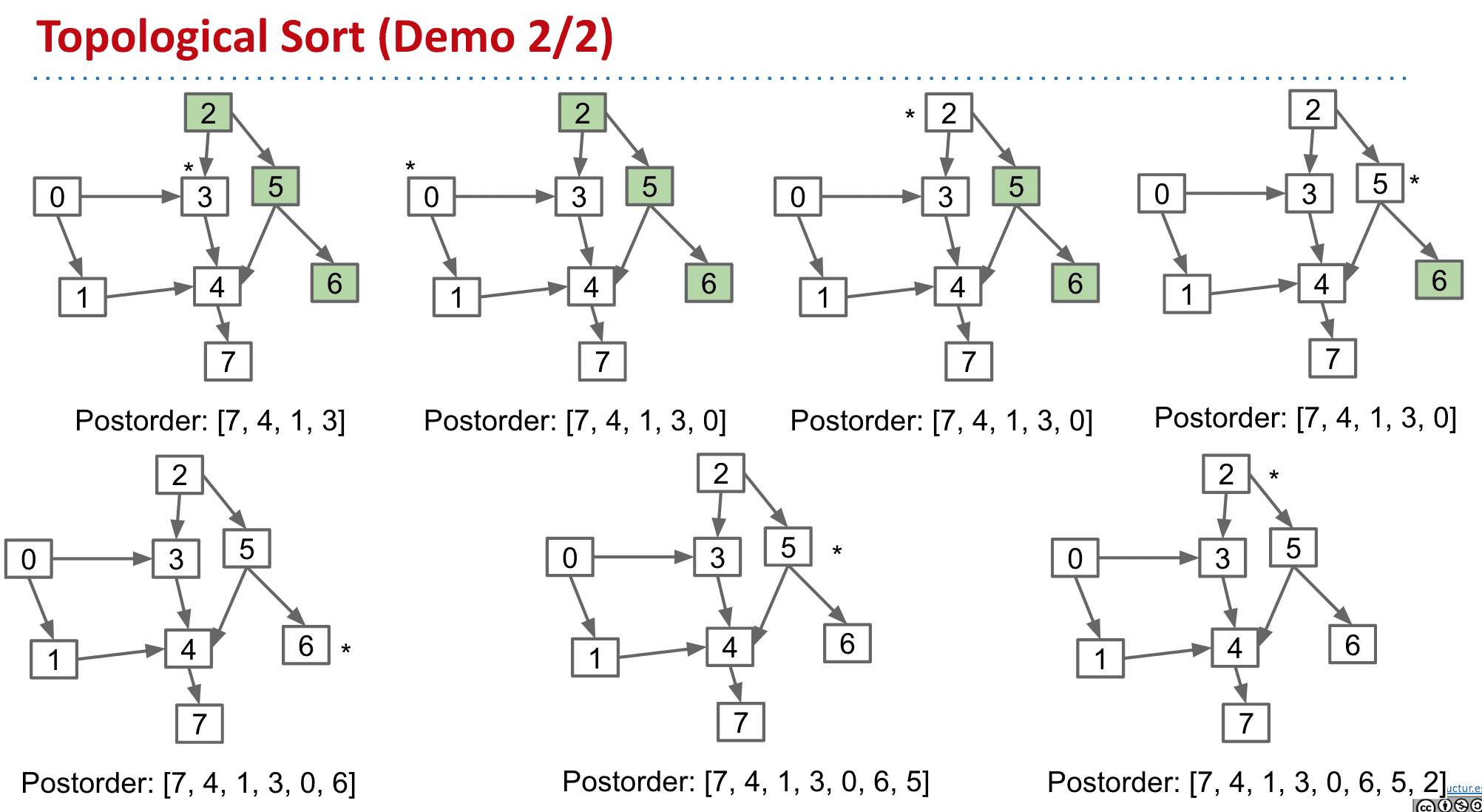
这样就得到了postorde: [7, 4, 1, 3, 0, 6, 5, 2]然后翻转就得到了Topological ordering:[2, 5, 6, 0, 3, 1, 4, 7]
之所以要使用Postorder再进行翻转的操作是因为,我们使用了DFS,也就是说先访问到的节点比较“深”那么也应该放在更后面的位置所以要倒序记录并翻转
之所以叫拓扑排序是因为相当于对节点的排序让他们以固定的顺序来指向
拓扑排序(Topological Order)是指,将一个有向无环图(Directed Acyclic Graph简称DAG)进行排序进而得到一个有序的线性序列
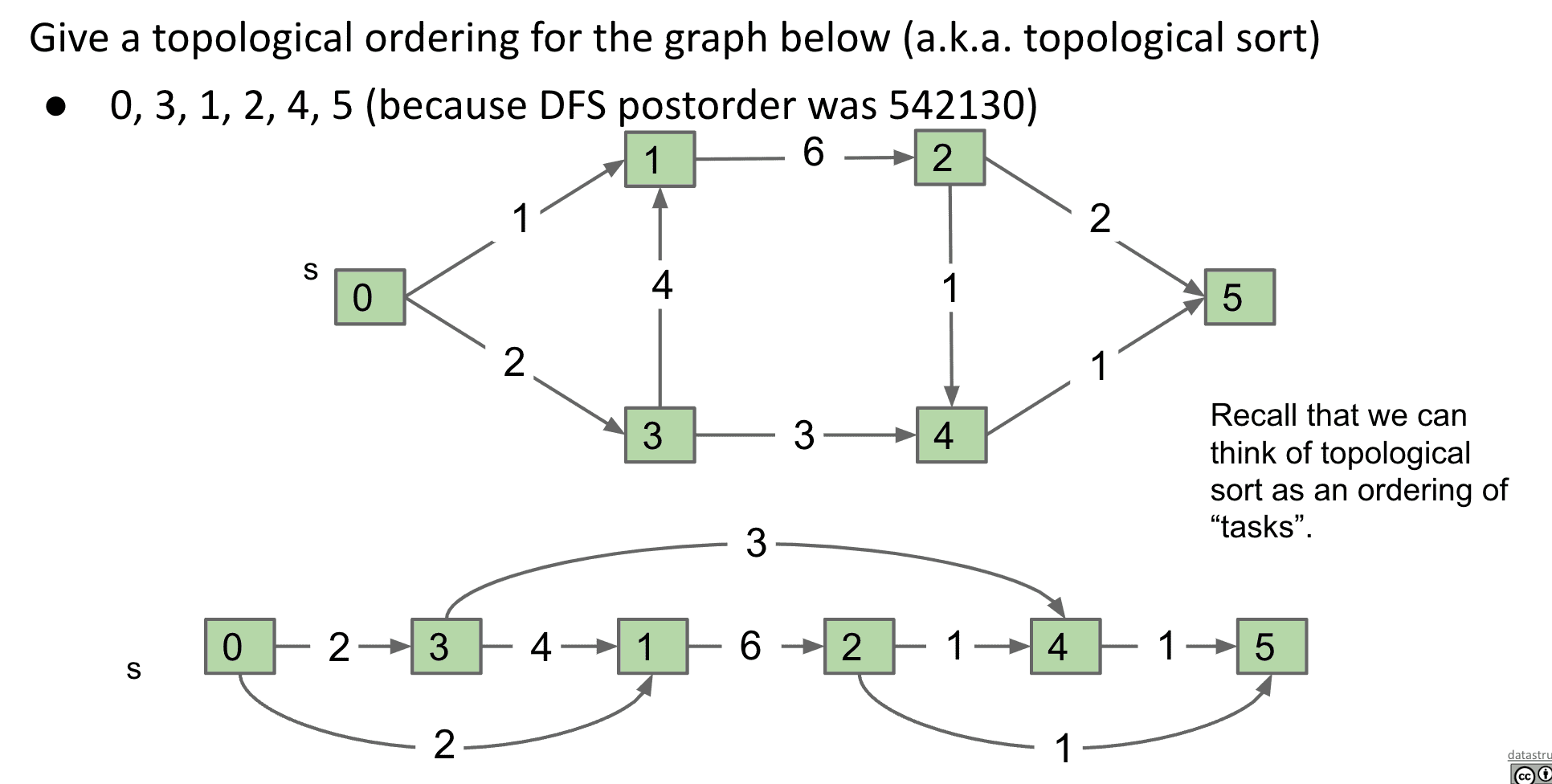
拓扑排序只适用于DAG(有向无环图),而且还有大量其他算法也只适用于DAG,向下面这个有环的图就不能使用拓扑排序
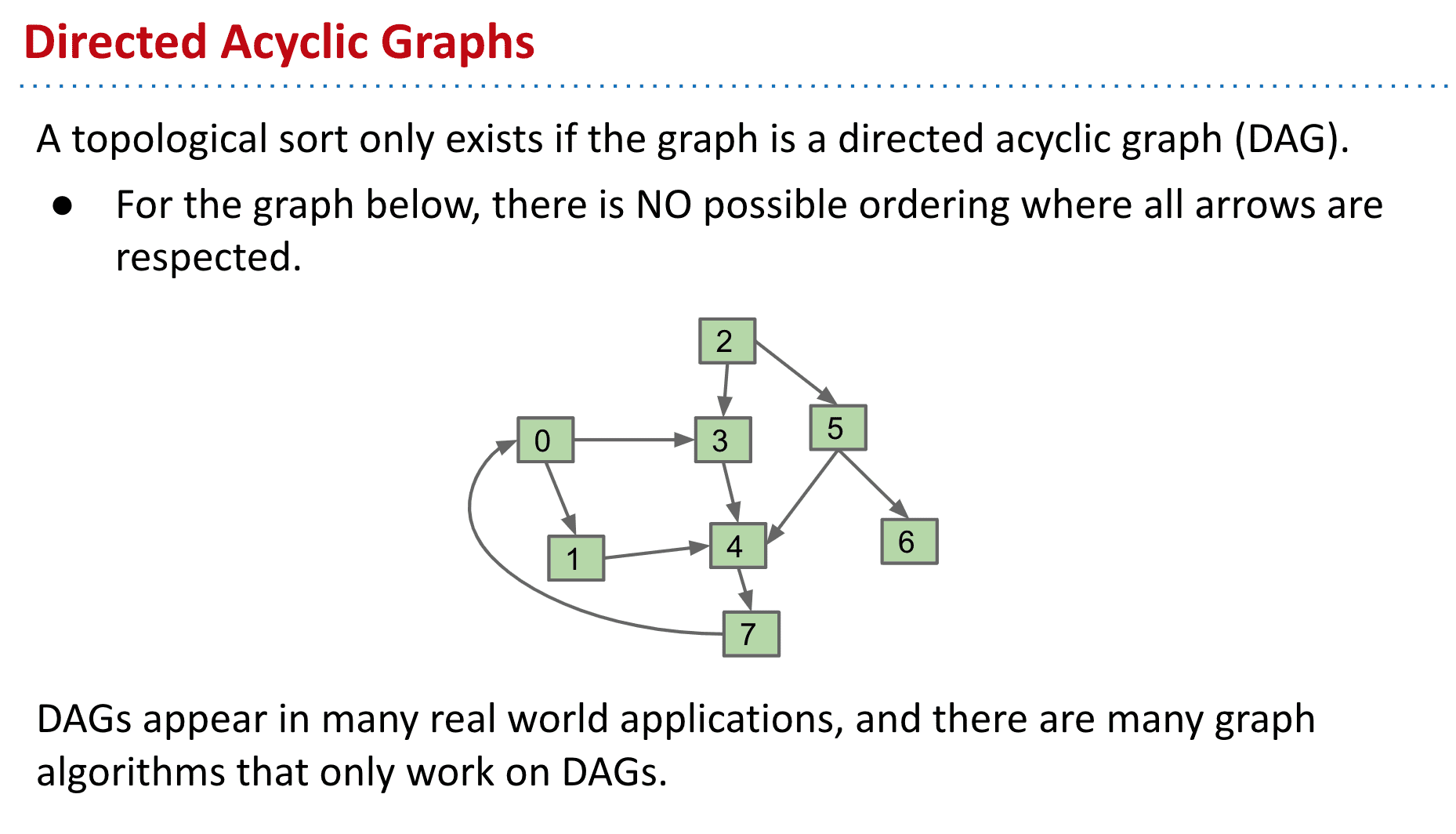
DAG的最短路径
像下面这的DAG可以使用Dijkstra’s algorithm,但一旦有负的权值就会失效了(因为Dijkstra’s algorithm不会访问标记过了的节点)
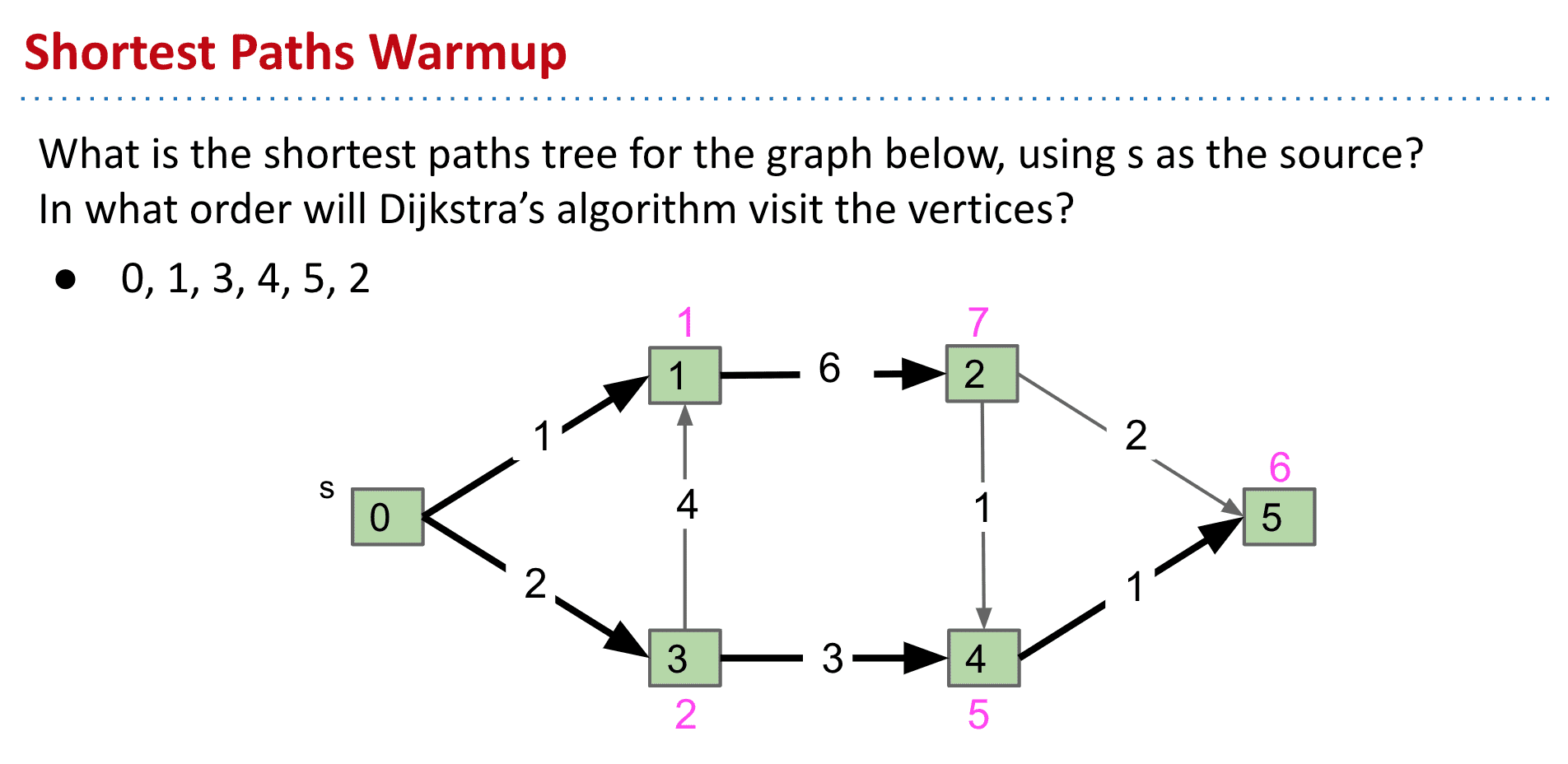
使用拓扑排序后再用类似Dijkstra’s algorithm的方式就可以做到处理带负权值的最短路径了(使用了拓扑排序后我们的走向是固定的,也就不用担心某个顶点的上游下游有没有负权值之类的了)
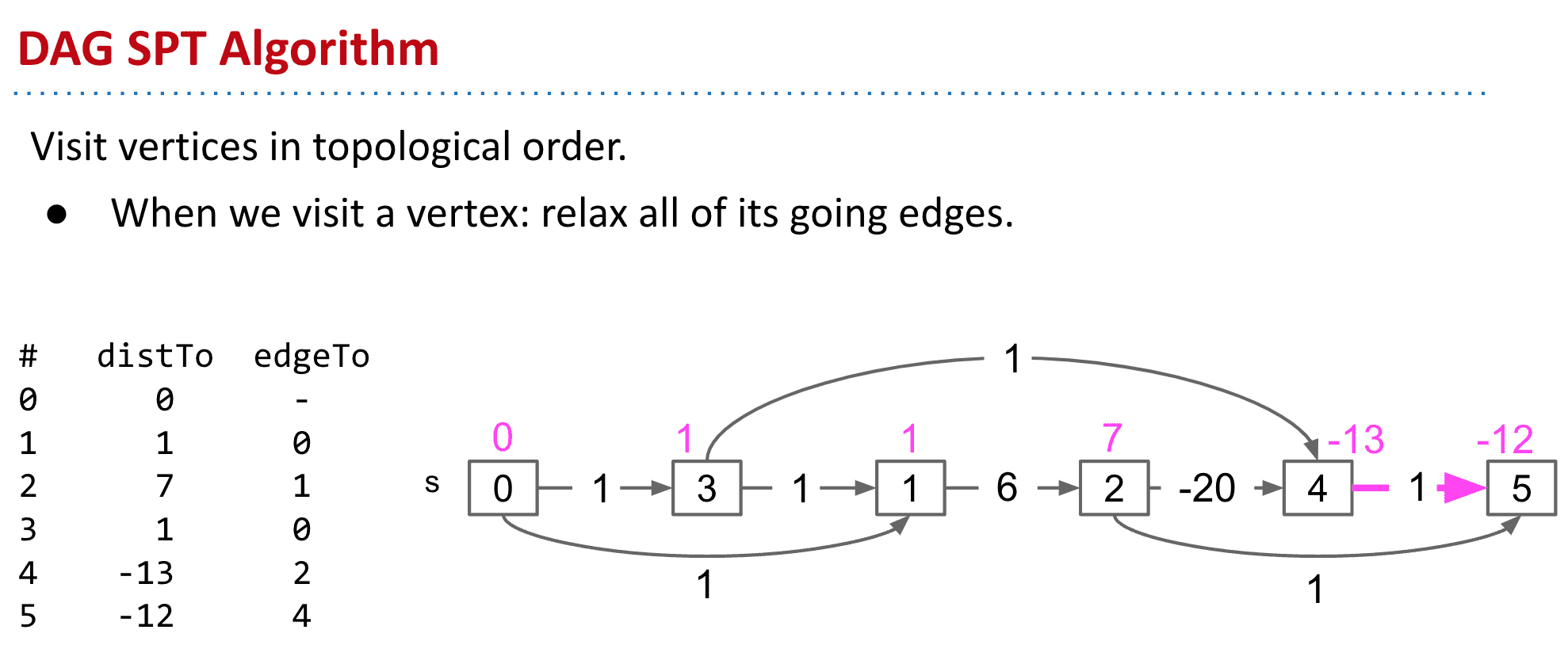
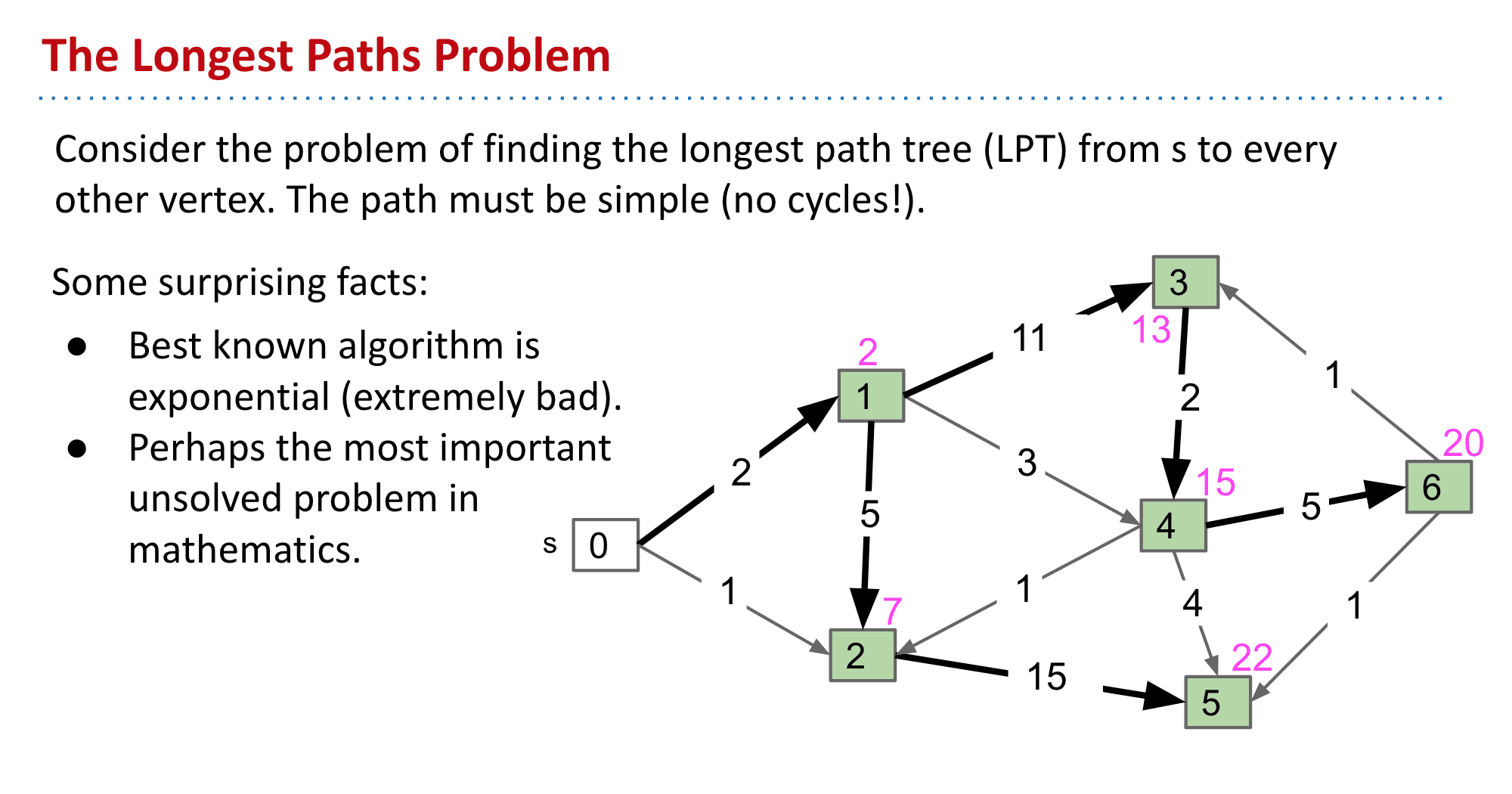
最长路径
这是个还没有很好未解决的数学问题,最好的算法也是指数级别的
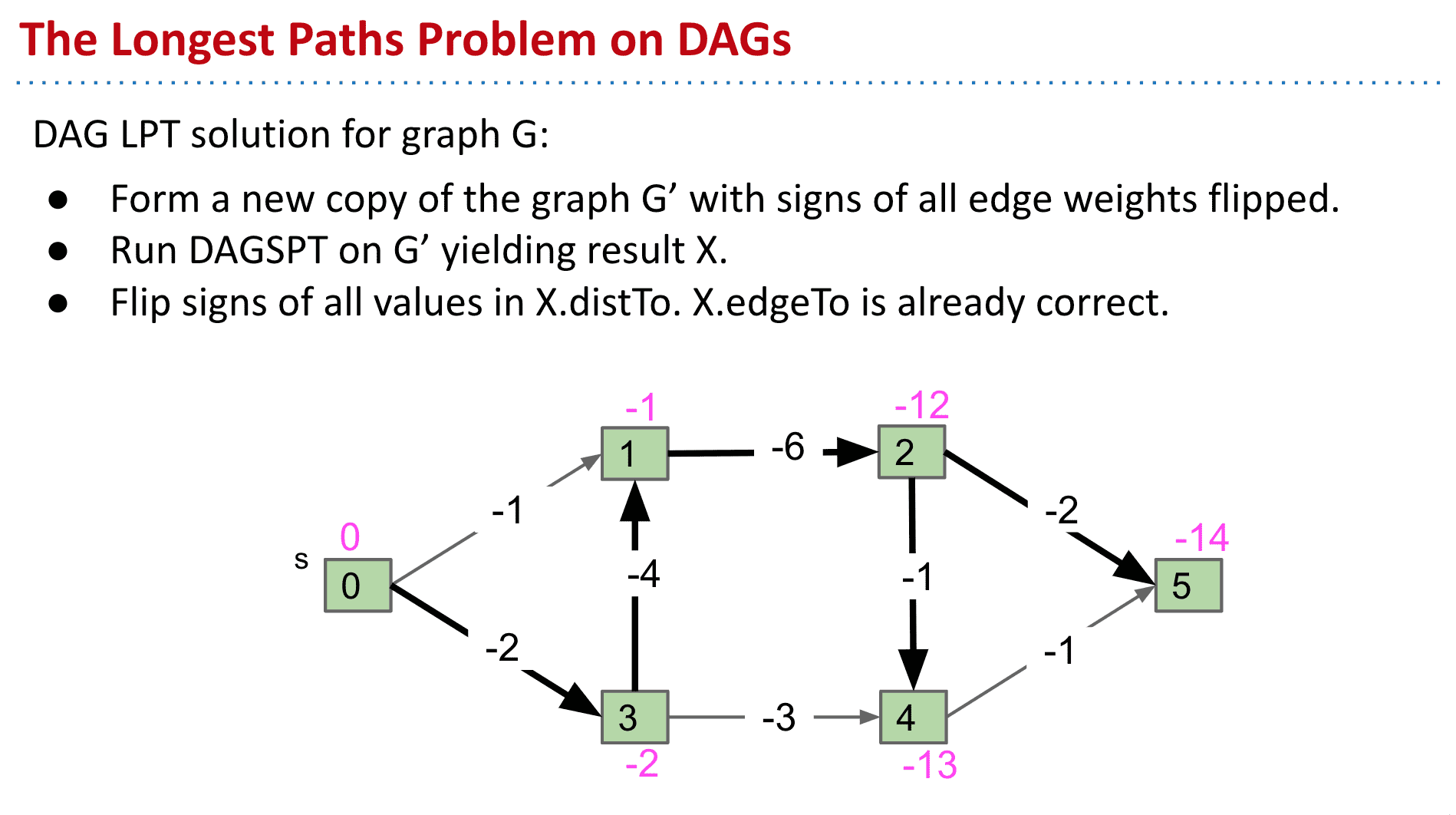
DAG中的解决办法

